In diesem Artikel erklären wir, was die horizontalen Asymptoten einer Funktion sind und wie sie berechnet werden. Darüber hinaus finden Sie mehrere Beispiele für diese Art von Asymptoten, um das Konzept vollständig zu verstehen. Darüber hinaus können Sie mit gelösten Übungen zu horizontalen Asymptoten üben.
Was ist eine horizontale Asymptote?
Eine horizontale Asymptote einer Funktion ist eine horizontale Linie, der sich ihr Graph auf unbestimmte Zeit nähert, ohne sie jemals zu kreuzen. Daher lautet die Gleichung für eine horizontale Asymptote y=k , wobei k der Wert der horizontalen Asymptote ist.
Das heißt, k ist eine horizontale Asymptote, wenn der Grenzwert der Funktion bei Annäherung von x an die Unendlichkeit gleich k ist.
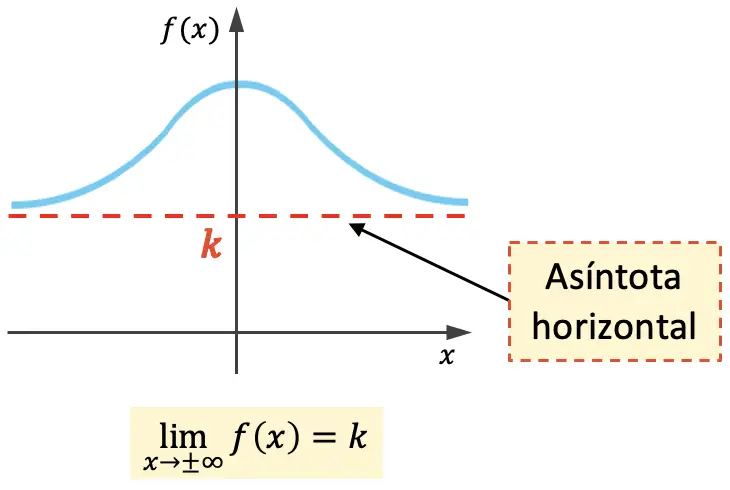
Die obige Funktion hat eine horizontale Asymptote auf beiden Seiten des Diagramms, aber eine Funktion kann nur eine horizontale Asymptote auf einer Seite haben:
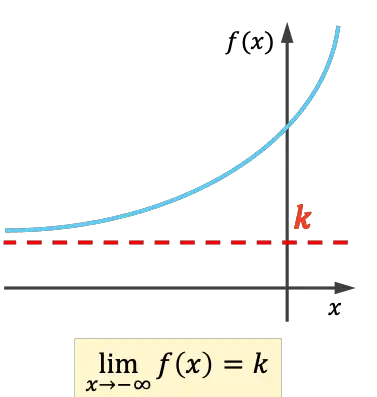
- Die Funktion hat eine linke horizontale Asymptote , wenn der Grenzwert mindestens bis Unendlich eine reelle Zahl ergibt.
- Die Funktion hat eine horizontale Asymptote nach rechts, wenn der Grenzwert auf plus Unendlich eine reelle Zahl ergibt.

So berechnen Sie die horizontale Asymptote einer Funktion
Um die horizontale Asymptote einer Funktion zu berechnen, müssen die folgenden Schritte befolgt werden:
- Berechnen Sie den Grenzwert der Funktion auf Unendlichkeiten (+∞ und -∞).
- Wenn eine Grenze bis Unendlich eine reelle Zahl (k) ergibt, ist die Gerade y=k eine horizontale Asymptote der Funktion.
- Wenn keiner der Grenzwerte einer reellen Zahl entspricht, hat die Funktion keine horizontalen Asymptoten.
Beispiel für eine horizontale Asymptote
Damit Sie ein Beispiel dafür sehen können, entfernen wir alle horizontalen Asymptoten aus der folgenden rationalen Funktion:
![]()
Um die horizontalen Asymptoten zu bestimmen, muss der Grenzwert bei minus Unendlich und bei plus Unendlich der Funktion berechnet werden:
![]()
![]()
➤ Siehe: So lösen Sie die unendliche Unbestimmtheit zwischen unendlich
Die beiden Grenzen im Unendlichen ergeben 1, also ist y=1 die einzige horizontale Asymptote der Funktion.
Unten ist die Funktion grafisch dargestellt. Wie Sie sehen können, kommt die Funktion y=1 sehr nahe (sowohl bei plus Unendlich als auch bei minus Unendlich), berührt es jedoch nie, da es sich um eine horizontale Asymptote handelt.

Hinweis: In einigen Sonderfällen schneidet die Funktion die horizontale Asymptote an einem oder mehreren Punkten, aber im Allgemeinen schneidet der Graph einer Funktion nie ihre Asymptoten.
Andererseits hat diese Funktion auch eine vertikale Asymptote bei x=1. Denn wie Sie dem Diagramm entnehmen können, kommt es der x=1-Linie sehr nahe, erreicht diesen Wert jedoch nie.
Probleme horizontaler Asymptoten gelöst
Übung 1
Finden Sie ggf. die horizontale Asymptote der folgenden Bruchfunktion:
![]()
Um die horizontalen Asymptoten der rationalen Funktion zu bestimmen, müssen die Grenzen im Unendlichen der Funktion berechnet werden:
![]()
![]()
In diesem Fall ist das Ergebnis der unbestimmten Form ∞/∞ die Division der Koeffizienten von x höchsten Grades, da Zähler und Nenner von gleicher Ordnung sind.
Die Grenzen bei plus Unendlich und minus Unendlich der Funktion ergeben 2, also ist y=2 eine horizontale Asymptote und die einzige, die die Funktion hat.
Übung 2
Finden Sie alle horizontalen Asymptoten der folgenden rationalen Funktion mit einer Wurzel:
![]()
Um die horizontalen Asymptoten der Funktion zu finden, berechnen wir zunächst den Grenzwert im positiven Unendlichen:
![]()
Und dann lösen wir den Grenzwert der Funktion auf negative Unendlich:
![]()
➤ Wenn Sie Zweifel daran haben, wie die Grenzen bis zur Unendlichkeit gelöst wurden, empfehlen wir Ihnen, den obigen Link zur Lösung der unendlichen Unbestimmtheit zwischen Unendlichkeiten zu lesen.
In diesem Fall haben wir zwei unterschiedliche Werte der Grenzen im Unendlichen erhalten. Die Funktion hat also zwei horizontale Asymptoten: y=3 ist eine horizontale Asymptote der Funktion rechts und y=-3 ist andererseits eine horizontale Asymptote der Funktion links.
Übung 3
Berechnen Sie die horizontalen Asymptoten der folgenden stückweise definierten Funktion:
![Rendered by QuickLaTeX.com \displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa168db8e7d068a6d331e40401a90da6_l3.png)
Um die horizontalen Asymptoten der Funktion zu berechnen, gibt es keine Formel, aber Sie müssen die Grenzen bis plus und minus unendlich berechnen.
Um den mindestens unendlichen Grenzwert zu finden, verwenden wir daher die im ersten Abschnitt definierte Funktion:
![]()
Somit ist die Linie y=0 eine horizontale Asymptote links von der Funktion.
Und jetzt berechnen wir den Grenzwert bei plus unendlich, indem wir die im zweiten Abschnitt definierte Funktion verwenden:
![]()
Somit ist die Linie y=1/2 eine horizontale Asymptote rechts von der Funktion.