Hermitesche (oder hermitesche) matrix

Auf dieser Seite erfahren Sie, was eine Hermitesche Matrix, auch Hermitesche Matrix genannt, ist. Sie finden Beispiele für hermitesche Matrizen, alle ihre Eigenschaften und die Form, die diese Matrizentypen haben, um sie perfekt zu verstehen. Abschließend erklären wir auch, wie man eine komplexe Matrix in die Summe einer hermiteschen Matrix plus einer antihermiteschen Matrix zerlegt.

Was ist eine hermitesche oder hermitesche Matrix?

Eine hermitesche Matrix , oder auch hermitesche Matrix genannt, ist eine quadratische Matrix mit komplexen Zahlen, die die Eigenschaft hat, gleich ihrer konjugierten Transponierten zu sein.

A=A^*

Gold

A^*

ist die konjugierte Transponierungsmatrix von

A

.

Aus Neugier wurde dieser Matrixtyp zu Ehren von Charles Hermite benannt, einem französischen Mathematiker des 19. Jahrhunderts, der wichtige mathematische Forschungen durchführte, insbesondere auf dem Gebiet der linearen Algebra.

Der Grund für die Benennung dieser Matrix war, dass sie zeigte, dass die Eigenwerte (oder Eigenwerte) dieser bestimmten Matrizen immer reelle Zahlen sind, aber wir werden dies in Eigenschaften hermitescher Matrizen ausführlicher erklären.

Schließlich kann diese Matrix manchmal auch als selbstadjungierte Matrix bezeichnet werden, obwohl dies sehr selten vorkommt.

Beispiele für hermitesche Matrizen

Nachdem wir die Definition der hermiteschen Matrix (oder Hermiteschen Matrix) gesehen haben, sehen wir uns einige Beispiele für hermitesche Matrizen unterschiedlicher Dimensionen an:

Beispiel einer hermiteschen Matrix der Ordnung 2×2

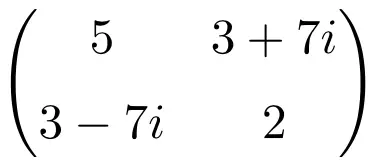
Hermitesche oder hermitesche Matrix der Dimension 2x2

Beispiel einer hermiteschen Matrix der Dimension 3 × 3

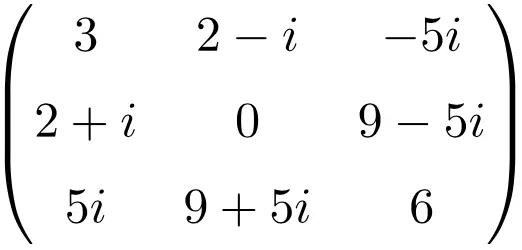
Hermitesche oder hermitesche Matrix der Dimension 3x3

Beispiel einer hermiteschen Matrix der Größe 4×4

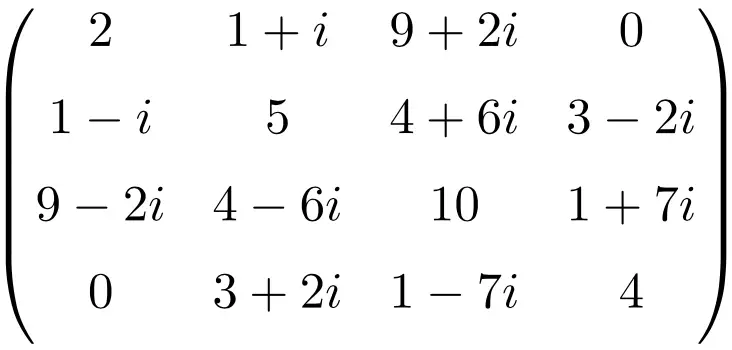
Hermitesche oder hermitesche Matrix der Dimension 4x4

Alle diese Matrizen sind hermitesch, da die konjugierte Transponierungsmatrix jeder Matrize gleich der Matrix selbst ist.

Struktur einer hermiteschen Matrix

Hermitesche Matrizen haben eine sehr leicht zu merkende Struktur: Sie bestehen aus reellen Zahlen auf der Hauptdiagonale, und das komplexe Element in der i-ten Zeile und der j-ten Spalte muss das Konjugat des Elements in der j-ten Zeile und sein die i-te Spalte.

Hier sind einige Beispiele für hermitesche Matrixstrukturen.

2×2 Hermitesche Struktur

\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}

3×3 Hermitesche Struktur

\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}

4×4 Hermitesche Struktur

\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}

Eigenschaften der hermiteschen Matrix

Wir werden nun sehen, welche Eigenschaften diese Art von quadratischer komplexer Matrix hat:

  • Jede hermitesche Matrix ist eine Normalmatrix . Obwohl nicht alle normalen Matrizen hermitesche Matrizen sind.
  • Jede hermitesche Matrix ist diagonalisierbar. Darüber hinaus enthält die resultierende Diagonalmatrix nur reelle Elemente.
  • Daher sind die Eigenwerte (oder Eigenwerte) einer hermiteschen Matrix immer reelle Zahlen. Diese Eigenschaft wurde von Charles Hermite entdeckt und aus diesem Grund hatte er die Ehre, diese ganz besondere Matrix Hermitian zu nennen.
  • Ebenso sind die Eigenräume einer hermiteschen Matrix zwei mal zwei orthogonal: Es gibt eine Orthonormalbasis von

    \mathbb{C}^n

    bestehend aus Eigenvektoren (Eigenvektoren) der Matrix.

  • Eine Matrix reeller Zahlen, das heißt, dass kein Element einen Imaginärteil hat, ist genau dann hermitesch, wenn es sich um eine symmetrische Matrix handelt. Wie zum Beispiel die 2×2-Identitätsmatrix .
  • Eine hermitesche Matrix kann als Summe einer realen symmetrischen Matrix und einer imaginären antisymmetrischen Matrix ausgedrückt werden.

A =B+Ci

  • Die Summe (oder Subtraktion) zweier hermitescher Matrizen ist gleich einer anderen hermiteschen Matrix, weil:

(A\pm B)^* = A^*\pm B^* = A \pm B

  • Das Ergebnis des Produkts einer hermiteschen Matrix mit einem Skalar ist eine weitere hermitesche Matrix, wenn der Skalar eine reelle Zahl ist.

(k \cdot A)^* = \overline{k}\cdot A^* = k \cdot A

  • Das Produkt zweier hermitescher Matrizen ist im Allgemeinen nicht mehr hermitesch. Das Produkt ist jedoch hermitesch, wenn die beiden Matrizen vertauschbar sind, d Matrizen:

(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B

  • Wenn eine hermitesche Matrix invertierbar ist, erweist sich auch ihre Umkehrung als hermitesche Matrix.

(A^{-1})^* = (A^*)^{-1} = A^{-1}

  • Die Determinante einer hermiteschen Matrix ist immer äquivalent zu einer reellen Zahl. Hier ist der Beweis dieser Eigenschaft:

det(A) = det(A^t) \ \longrightarrow \ det(A^*) = \overline{det(A)}

Durstig

A = A^*

:

det(A) = \overline{det(A)}

Damit diese Bedingung erfüllt ist, muss die Determinante einer hermiteschen Matrix unbedingt eine reelle Zahl sein. Auf diese Weise ist das Konjugat des Ergebnisses gleich dem Ergebnis selbst.

Zerlegung einer komplexen Matrix in eine hermitesche Matrix und eine antihermitesche Matrix

Jede Matrix mit komplexen Elementen kann in die Summe einer hermiteschen Matrix und einer weiteren antihermiteschen Matrix zerlegt werden. Dazu müssen Sie jedoch die folgenden Besonderheiten dieser Matrizentypen kennen:

  • Die Summe einer quadratischen komplexen Matrix plus ihrer transponierten Konjugierten ergibt eine hermitesche Matrix.

C + C^* = \text{Matriz Hermitiana}

  • Der Unterschied zwischen einer quadratischen komplexen Matrix und ihrem transponierten Konjugat ergibt eine antihermitesche (oder antihermitesche) Matrix.

C - C^* = \text{Matriz Antihermitiana}

  • Daher können alle komplexen Matrizen in die Summe einer hermiteschen Matrix und einer antihermiteschen Matrix zerlegt werden. Dieser Satz ist als Teoplitz-Zerlegung bekannt:

\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}

Dabei ist C die komplexe Matrix, die wir zerlegen möchten, C* ihr transponiertes Konjugat und schließlich sind A und B die hermitesche bzw. antihermitesche Matrize, in die die Matrix C zerlegt wird.

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen