Auf dieser Seite wird erklärt, was die Schnittpunkte (oder Schnittpunkte) einer Funktion mit den kartesischen Achsen sind und wie man sie berechnet. Darüber hinaus finden Sie mehrere Beispiele, um vollständig zu verstehen, wie sie gefunden werden, und Sie können sogar mit Schritt für Schritt gelösten Übungen üben.
Was sind die Schnittpunkte (oder Schnittpunkte) einer Funktion mit den Achsen?
Bevor wir sehen, wie sie berechnet werden, erinnern wir uns an die Schnittpunkte einer Funktion mit den Achsen.
Schnittpunkte oder Achsenschnittpunkte sind die Punkte, an denen die Darstellung einer Funktion die Koordinatenachsen schneidet, also die Punkte im Diagramm, die auf der X-Achse und auf der L-Achse binden. Y-Achse.
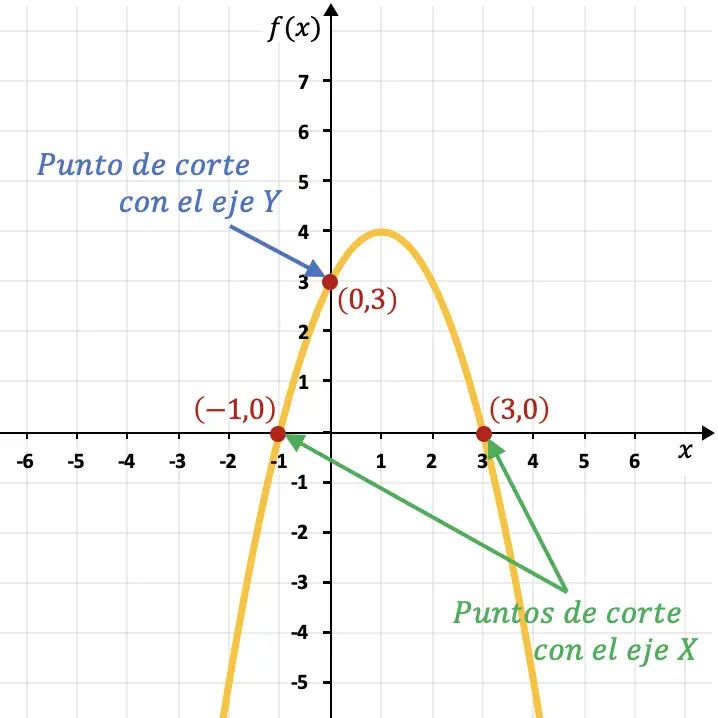
Beispielsweise schneidet die Parabel im folgenden Diagramm die Y-Achse am Punkt (0,3) und die X-Achse an den Punkten (-1,0) und (3,0).
Schnittpunkt einer Funktion mit der X-Achse
Die zweite Koordinate der Schnittpunkte einer Funktion mit der X-Achse ist immer 0, daher:
Die Grenzwerte jeder x-Achsenfunktion OX haben die Form
![]()
und kann durch Lösen der folgenden Gleichung berechnet werden:
![]()
Manchmal können wir beim Lösen dieser Gleichung zwei (oder mehr) Lösungen erhalten, was bedeutet, dass die Funktion die X-Achse zwei (oder mehr) Mal schneidet. Wenn die Gleichung hingegen keine Lösung hat, bedeutet dies, dass die Funktion die X-Achse nicht schneidet.
Schnittpunkt einer Funktion mit der Y-Achse
Die erste Koordinate der Schnittpunkte einer Funktion mit der Y-Achse ist immer 0, daher:
Der Grenzwert jeder Funktion mit der y-Achse OY hat die Form
![]()
, und kann durch Berechnen des Bildes der Funktion bei x=0 ermittelt werden:
![]()
Im Gegensatz zu Haltepunkten auf der X-Achse kann es auf der Y-Achse nur einen Haltepunkt geben.
Beispiel für die Berechnung der Grenzwerte einer Funktion mit den Achsen
Damit Sie keine Zweifel haben, sehen wir unten ein Beispiel, wie man die Schnittpunkte einer Funktion mit den kartesischen Achsen findet:
- Ermitteln Sie numerisch die Grenzwerte der folgenden Funktion:
![]()
Wir berechnen zunächst den Cutoff-Punkt der Funktion mit der x-Achse. Die zweite Komponente des Schnittpunkts mit der X-Achse ist immer gleich 0, also vom Typ
![]()
. Weil f(x) auf der OX-Achse immer gleich 0 ist. Um also die andere Komponente des Punktes zu finden, müssen wir die Gleichung lösen
![]()
![]()
![]()
![]()
![]()
Der Schnittpunkt mit der X-Achse ist also:
![]()
Jetzt suchen wir den Schnittpunkt mit der y-Achse. Die erste Komponente des Schnittpunkts mit der Y-Achse ist immer gleich 0, d. h. der Punkt ist vom Typ
![]()
. Da sich die unabhängige Variable x immer auf der Y-Achse löscht. Um also die andere Koordinate des Punktes zu finden, müssen wir berechnen
![]()
![]()
Der Schnittpunkt mit der Y-Achse ist also:
![]()
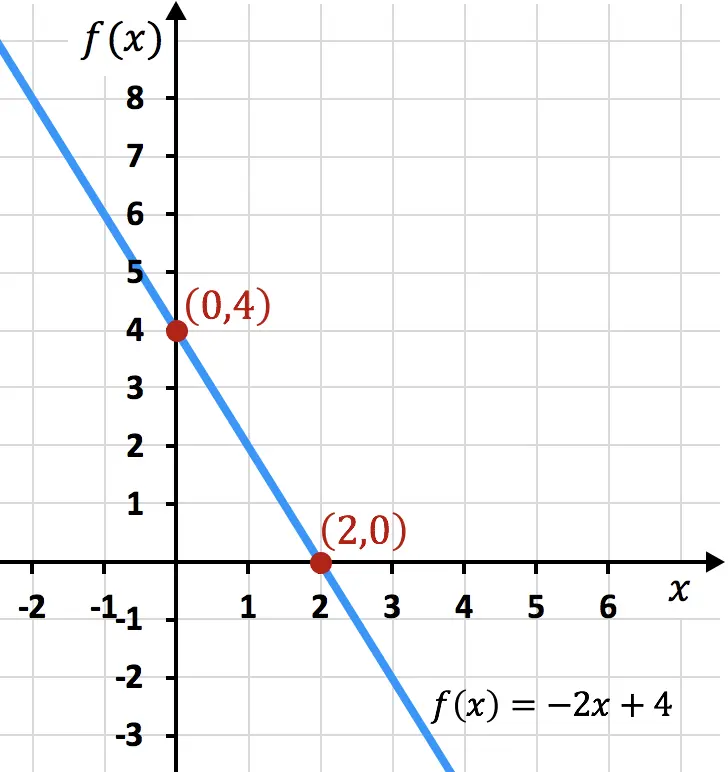
Unten sehen Sie die Beispielfunktion grafisch dargestellt. Sie können sehen, dass die gefundenen Schwellenwerte mit denen in der Grafik übereinstimmen:
Gelöste Übungen für Schnittpunkte einer Funktion mit Achsen
Übung 1
Bestimmen Sie die Schnittpunkte mit den Koordinatenachsen der folgenden Funktion:
![]()
Schnittpunkt mit X-Achse
Um den Schnittpunkt der Funktion mit der X-Achse zu finden, ist eine Lösung erforderlich
![]()
![]()
![]()
![]()
![]()
Der Schnittpunkt der Funktion mit der X-Achse ist also:
![]()
Schnittpunkt mit Y-Achse
Um den Schnittpunkt mit der Y-Achse zu finden, müssen Sie rechnen
![]()
![]()
Der Schnittpunkt der Funktion mit der Y-Achse ist also:
![]()
Übung 2
Finden Sie die Schnittpunkte mit den kartesischen Achsen der folgenden affinen Funktion:
![]()
Schnittpunkt mit X-Achse
Um den Grenzpunkt der Funktion mit der OX-Achse zu finden, müssen wir die Funktion gleich Null setzen und die resultierende Gleichung lösen:
![]()
![]()
![]()
![]()
Der Schnittpunkt der Funktion mit der Abszissenachse ist also:
![]()
Schnittpunkt mit Y-Achse
Um den Cutoff-Punkt mit der OY-Achse zu finden, müssen wir berechnen
![]()
![]()
Der Schnittpunkt der Funktion mit der Rechnerachse ist also:
![]()
Übung 3
Berechnen Sie die Grenzwerte mit den Achsen der folgenden quadratischen Funktion:
![]()
Schnittpunkt mit X-Achse
Um den Schnittpunkt der Funktion mit der X-Achse zu finden, ist eine Lösung erforderlich
![]()
![]()
![]()
In diesem Fall müssen wir eine quadratische Gleichung lösen, also wenden wir die Formel an:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47048fdd48ce98ba99629edf5a379f76_l3.png)
Wir haben zwei Lösungen der quadratischen Gleichung erhalten, sodass die Funktion die X-Achse in zwei Punkten schneidet:
![]()
Schnittpunkt mit Y-Achse
Um andererseits den Schnittpunkt mit der Y-Achse zu bestimmen, ist eine Berechnung erforderlich
![]()
![]()
Daher ist der einzige Schnittpunkt der Funktion mit der Y-Achse:
![]()
Übung 4
Finden Sie die Schnittpunkte mit den Achsen der kartesischen Ebene der folgenden rationalen Funktion:
![]()
Schnittpunkt mit X-Achse
Um den Schnittpunkt der Funktion mit der X-Achse zu finden, ist eine Lösung erforderlich
![]()
![]()
![]()
![]()
![]()
![]()
5 ist nicht äquivalent zu 0, daher hat die Gleichung keine Lösung und es gibt daher keinen Schnittpunkt zwischen der Funktion und der X-Achse.
Schnittpunkt mit Y-Achse
Um den Schnittpunkt mit der Y-Achse zu finden, müssen Sie rechnen
![]()
![]()
Jede durch Null geteilte Zahl ist eine Unbestimmtheit, die Unendlich ergibt. Daher erstreckt sich die Funktion an keinem Punkt über die Y-Achse hinaus.
Kurz gesagt, die Übungsfunktion hat keine Schnittpunkte mit den Achsen , das heißt, ihr Graph verläuft an keinem Punkt durch die X-Achse oder die Y-Achse.
Übung 5
Berechnen Sie die Grenzwerte mit den Achsen der folgenden Funktion dritten Grades:
![]()
Schnittpunkt mit X-Achse
Um den Schnittpunkt der Funktion mit der X-Achse zu finden, ist eine Lösung erforderlich
![]()
![]()
![]()
Beide Terme der Gleichung haben ein x , mit dem wir einen gemeinsamen Faktor extrahieren können:
![]()
Damit die vorherige Gleichheit erfüllt ist, muss einer der Faktoren 0 sein. Daher setzen wir jeden Faktor gleich Null, um alle möglichen Lösungen zu erhalten:
![Rendered by QuickLaTeX.com \displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-37febaed85a502533604305b9009611d_l3.png)
Wir haben daher drei Lösungen der Gleichung dritten Grades erhalten, sodass die Funktion die X-Achse in drei Punkte schneidet:
![]()
Schnittpunkt mit Y-Achse
Um den Schnittpunkt mit der Y-Achse zu berechnen, müssen Sie rechnen
![]()
![]()
Daher ist der einzige Schnittpunkt der Funktion mit der Y-Achse der Koordinatenursprung (0,0):
![]()
Beachten Sie, dass wir diesen Punkt bereits bei der Berechnung des Schnittpunkts mit der X-Achse gefunden hatten, da die Funktion an diesem Punkt mit beiden Achsen gleichzeitig schneidet.