Gleichungspunkt – Steigung der Geraden

Auf dieser Seite finden Sie die Formel für die Punkt-Steigungsgleichung der Geraden und auch die verschiedenen Möglichkeiten, sie zu berechnen. Darüber hinaus können Sie sich mehrere Beispiele ansehen und mit Schritt für Schritt gelösten Übungen üben.

Formel für die Punkt-Steigungsgleichung der Geraden

Die Punkt-Steigungsgleichung einer Geraden ist eine Möglichkeit, eine Gerade mathematisch auszudrücken. Insbesondere benötigen Sie nur die Steigung und die Koordinaten eines Punktes auf der Geraden, um die Punkt-Steigung-Gleichung einer Geraden zu ermitteln.

Die Formel für die Punkt-Steigungsgleichung der Geraden lautet wie folgt:

$y-y_0=m(x-x_0)$

Gold

$m$

ist die Steigung der Geraden und

$x_0, y_0$

sind die Koordinaten eines Punktes auf der Geraden

$P(x_0,y_0).$

Sehen wir uns anhand eines Beispiels an , wie die Punkt-Steigungsgleichung der Geraden berechnet wird :

Schreiben Sie die Punkt-Steigungsgleichung der Geraden, die durch den Punkt verläuft
$P(2,-1)$

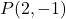
und Steigung m=3.

Die Formel für die Punkt-Steigungsgleichung der Geraden lautet wie folgt:

$y-y_0=m(x-x_0)$

In diesem Fall besagt die Aussage, dass die Steigung der Geraden m=3 beträgt, sodass die Gleichung der Geraden wie folgt lautet:

$y-y_0=3(x-x_0)$

Darüber hinaus wissen wir auch, dass die Gerade durch den Punkt verläuft

$P(2,-1)$

, wir müssen daher die Koordinaten dieses Punktes in die Gleichung einsetzen:

$P(2,-1)$

$y-y_0=3(x-x_0) \ \xrightarrow{x_0=2 \ ; \ y_0=-1} \ y-(-1)=3(x-2)$

Die Punkt-Steigungsgleichung der Geraden lautet daher:

$\bm{y+1=3(x-2)}$

Bedenken Sie, dass es neben der Punkt-Steigungsgleichung noch andere Möglichkeiten gibt, eine Gerade analytisch auszudrücken: die Vektorgleichung, parametrische Gleichungen, die kontinuierliche Gleichung, die implizite (oder allgemeine) Gleichung und die explizite Gleichung einer Geraden. Wenn Sie mehr Interesse haben, können Sie auf unserer Website nachsehen, um was es sich dabei handelt.

Was bedeutet die Steigung einer Geraden?

Wie wir bei der Definition der Punkt-Steigungsgleichung einer Geraden gesehen haben, ist der Parameter

$m$

ist die Steigung der Geraden. Aber wirklich … was bedeutet die Steigung einer Linie? Sehen wir uns dies anhand der grafischen Darstellung einer Linie an:

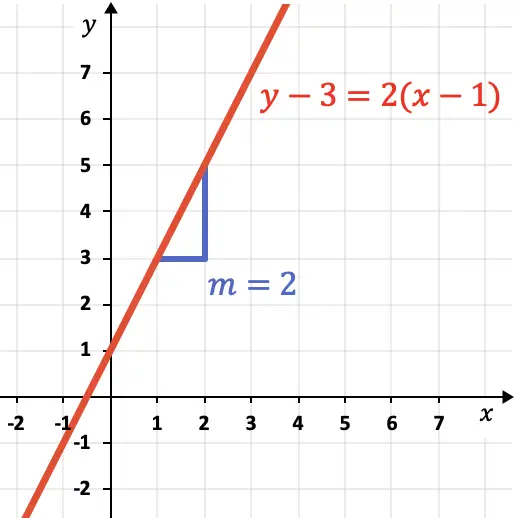
Wie lautet die Punkt-Steigungsgleichung einer Geraden?

Die Steigung der Linie gibt ihre Steilheit an. Wie Sie der Diagrammlinie entnehmen können,

$m$

ist gleich 2, da die Linie um 2 vertikale Einheiten für 1 horizontale Einheit ansteigt.

Offensichtlich nimmt die Funktion zu, wenn die Steigung positiv ist (steigt), wenn die Steigung negativ ist, nimmt die Funktion ab (sinkt).

So berechnen Sie die Steigung einer Geraden

Darüber hinaus gibt es drei verschiedene Möglichkeiten, die Steigung einer Geraden numerisch zu bestimmen:

Gegeben seien zwei unterschiedliche Punkte auf der Geraden
$P_1(x_1,y_1)$

Und

$P_2(x_2,y_2),$

Die Steigung der Geraden ist gleich:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Ja
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

ist der Richtungsvektor der Geraden, ihre Steigung ist:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Ja
$\alpha$

ist der Winkel, den die Linie mit der Abszissenachse (X-Achse) bildet, die Steigung der Linie entspricht dem Tangens dieses Winkels:

$m = \text{tg}(\alpha )$

Formel für die explizite Gleichung der Geraden

Relative Position der Linien

Schließlich wird die Steigung einer Geraden auch genutzt, um die Beziehung zwischen mehreren Geraden zu kennen. Da zwei parallele Geraden die gleiche Steigung haben und andererseits die Steigung einer Geraden der negative Kehrwert der Steigung einer anderen Geraden ist, bedeutet dies, dass diese beiden Geraden senkrecht zueinander stehen.

Berechnen Sie die Punkt-Steigungsgleichung der Geraden, die durch zwei Punkte verläuft

Ein sehr häufiges Problem besteht darin, die Punkt-Steigungsgleichung aus zwei zur Geraden gehörenden Punkten zu ermitteln. Sehen wir uns anhand eines Beispiels an, wie es gelöst wird:

Finden Sie die Punkt-Steigungsgleichung der Geraden, die durch die folgenden zwei Punkte verläuft:

$P_1(5,2) \qquad P_2(3,6)$

Um die Punkt-Steigungsgleichung der Geraden zu finden, müssen wir die Steigung der Geraden bestimmen. Also berechnen wir die Steigung der Linie mit der Doppelpunktformel:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{6-2}{3-5} = \cfrac{4}{-2}= -2$

Somit lautet die Punkt-Steigungsgleichung der Geraden wie folgt:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Daher müssen wir nur die kartesischen Koordinaten eines Punktes auf der Geraden in die Gleichung einsetzen:

$P_1(5,2)$

$y-y_0=-2(x-x_0) \ \xrightarrow{x_0=5 \ ; \ y_0=2} \ y-2=-2(x-5)$

$\bm{y-2=-2(x-5)}$

Es ist auch gut, wenn wir den anderen Punkt der Aussage in die Gleichung der Geraden einsetzen:

$P_1(3,6)$

$y-6=-2(x-3)$

Finden Sie die Punkt-Steigungsgleichung einer Linie aus dem Diagramm

Wie wir in den obigen Abschnitten gesehen haben, gibt es mehrere Möglichkeiten, die Punkt-Steigungsgleichung einer Geraden numerisch zu ermitteln. Es ist jedoch auch grafisch zu finden. Sehen wir uns anhand eines Beispiels an, wie das geht:

Bestimmen Sie die Punkt-Steigungsgleichung der in der folgenden Grafik gezeigten Linie:

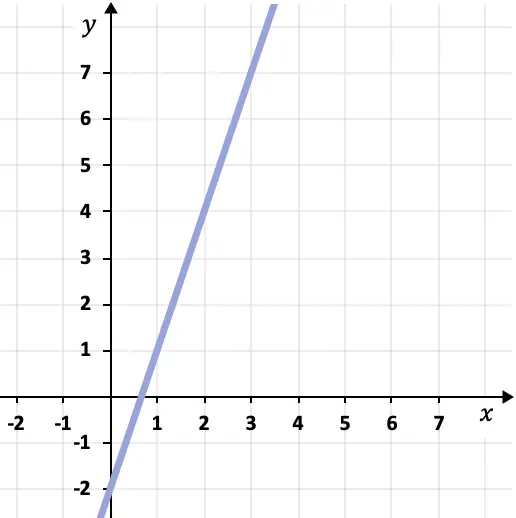
Um die Punkt-Steigungsgleichung für die gezeichnete Linie zu bestimmen, müssen wir deren Steigung und einen Punkt auf der Linie ermitteln.

In diesem Fall beträgt die Steigung der Linie 3, da die Linie für jede horizontale Einheit um 3 vertikale Einheiten ansteigt.

$m = 3$

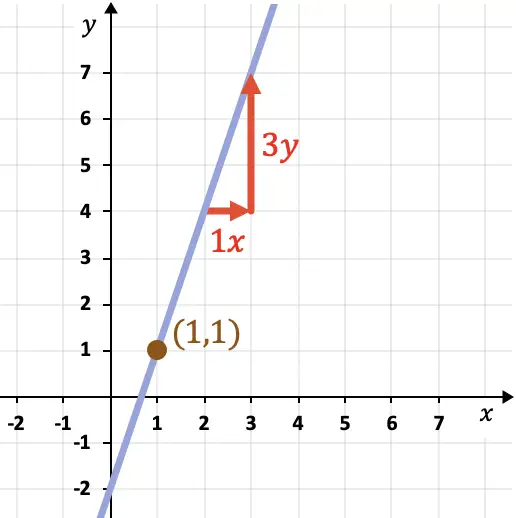
Als nächstes brauchen wir einen Punkt auf der Linie. Dazu können wir einen beliebigen Punkt im Diagramm auswählen, durch den die Gerade verläuft, beispielsweise den Punkt (1,1).

$P(1,1)$

Daher können wir nun die Punkt-Steigungsgleichung der Geraden finden, indem wir ihre Formel anwenden:

$y-y_0=m(x-x_0)$

$y-1=3(x-1)$

Bestimmen Sie grafisch die Steigung des Gleichungspunktes einer Geraden

Probleme mit der Punkt-Steigung-Gleichung gelöst

Übung 1

Schreiben Sie die Punkt-Steigungsgleichung der Geraden, die durch den Punkt verläuft

$P(1,4)$

und seine Steigung ist

$m=-2.$

siehe Lösung

Die Formel für die Punkt-Steigungsgleichung der Geraden lautet:

$y-y_0=m(x-x_0)$

In diesem Fall besagt die Aussage, dass die Steigung der Geraden m=-2 ist, sodass die Gleichung der Geraden wie folgt lautet:

$y-y_0=-2(x-x_0)$

Darüber hinaus wissen wir aus der Aussage auch, dass die Gerade durch den Punkt verläuft

$P(1,4)$

, es genügt also, die Koordinaten des Punktes in die Geradengleichung einzusetzen:

$P(1,4)$

$\bm{y-4=-2(x-1)}$

Übung 2

Wie lautet die Punkt-Steigungsgleichung der Geraden, die durch die folgenden zwei Punkte verläuft?

$P_1(1,6) \qquad P_2(4,0)$

siehe Lösung

Um die Punkt-Steigungsgleichung der Geraden zu finden, müssen wir die Steigung der Geraden bestimmen. Wir berechnen daher die Steigung der Geraden mit ihrer Formel:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{0-6}{4-1} = \cfrac{-6}{3}= -2$

Somit lautet die Punkt-Steigungsgleichung der Geraden wie folgt:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Daher müssen wir nur die Koordinaten eines Punktes auf der Geraden in die Gleichung einsetzen:

$P_1(1,6)$

$\bm{y-6=-2(x-1)}$

Es wäre auch richtig gewesen, den anderen Punkt der Aussage in die Gleichung einzubeziehen:

$y=-2(x-4)$

Übung 3

Finden Sie die Punkt-Steigungsgleichung der Geraden, die durch die folgenden zwei Punkte verläuft:

$P_1(1,-2) \qquad P_2(2,3)$

siehe Lösung

Um die Punkt-Steigungsgleichung der Geraden zu finden, müssen Sie zunächst deren Steigung berechnen:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{3-(-2)}{2-1} = \cfrac{3+2}{1}=\cfrac{5}{1}= 5$

Somit lautet die Punkt-Steigungsgleichung der Geraden wie folgt:

$y-y_0=m(x-x_0)$

$y-y_0=5(x-x_0)$

Daher müssen wir nur die Koordinaten eines Punktes auf der Geraden in die Gleichung einsetzen:

$P_1(1,-2)$

$y-(-2)=5(x-1)$

$\bm{y+2=5(x-1)}$

Es ist auch richtig, den anderen Punkt der Aussage in die Geradengleichung einzufügen:

$y-3=5(x-2)$

Übung 4

Berechnen Sie die Punkt-Steigungsgleichung für die Linie, die mit der X-Achse einen Winkel von 45° bildet und durch den Koordinatenursprung verläuft.

siehe Lösung

Wenn die Linie mit der OX-Achse einen Winkel von 45 Grad bildet, beträgt ihre Steigung:

$m = \text{tg}(45º) = 1$

$y-y_0=1(x-x_0)$

$y-y_0=x-x_0$

Und sobald wir die Steigung der Geraden kennen, können wir die Punkt-Steigungsgleichung finden, indem wir einen Punkt auf der Geraden in die Gleichung einsetzen. Darüber hinaus sagt uns die Anweisung, dass die Linie durch den Koordinatenursprung verläuft, was bedeutet, dass sie durch den Punkt (0,0) verläuft. Noch:

$P(0,0)$