Gleichungen ersten Grades oder lineare Gleichungen sind die Grundlage der Algebra , denn wenn Sie sie nicht verstehen, wird es für Sie sehr schwierig sein, komplexere Gleichungen zu verstehen. Die Besonderheit dieser Art von Gleichungen besteht also darin, dass der Literalteil der Monome keinen Exponenten haben kann. Daher finden wir in einer linearen Gleichung nur Monome ohne Literalteil und Monome mit Literalteil ohne Exponenten, wie zum Beispiel: 3 + x = -5 – 3x .
Beachten Sie auch, dass diese Gleichungen normalerweise eine eindeutige Lösung haben, auch wenn dies möglicherweise nicht der Fall ist. Um zu wissen, welchen Fall wir vor uns haben, müssen wir die Gleichung lösen und am Ende das Ergebnis analysieren . Wenn wir also eine unmögliche Gleichheit wie 2 = 0 erhalten, dann hat die Gleichung keine Lösung. Wenn wir andererseits eine Gleichung erhalten, die immer wahr ist, dann ist die Lösung äquivalent zu allen reellen Zahlen. Und schließlich, wenn wir am Ende die Gleichheit von X und einem numerischen Wert erhalten, erhalten wir in diesem Fall ein eindeutiges Ergebnis.
Verfahren zum Lösen einer linearen Gleichung
Das Lösen einer Gleichung entspricht der Berechnung des Werts einer Variablen, dargestellt durch einen Buchstaben (x, y, a, b…). Um diesen Wert zu finden, müssen wir die folgenden Schritte ausführen:
- Klammern und Brüche lösen: Zunächst entfernen wir alle Klammern und Nenner, um eine leichter verständliche Gleichung zu erhalten. Da wir direkt erkennen können, welche Begriffe mit dem Unbekannten einhergehen und welche nicht, können wir mit dieser Lektüre den Ausdruck problemlos weiter auflösen.
- Vereinfachen wir den Ausdruck: Wir gruppieren ähnliche Begriffe (unabhängige Begriffe einerseits und Begriffe mit x andererseits). Also lassen wir auf der einen Seite die Zahlen, die das Unbekannte haben, und geben die anderen Zahlen auf die gegenüberliegende Seite weiter. Aber denken Sie daran: Um ihre Seiten zu wechseln, müssen wir ihr Vorzeichen ändern.
- Auf jeder Seite operieren: Wir führen alle Operationen in der folgenden Reihenfolge aus: Potenzen/Wurzeln, Multiplikationen/Divisionen und Additionen/Subtraktionen. Dies machen wir so lange, bis wir auf jeder Seite einen einzigen Term erhalten, und am Ende erhalten wir eine Gleichung mit der gleichen Struktur wie dieser: 4x = 8.
- Isolieren Sie die Variable: Übergeben Sie schließlich einfach den Wert, der dem Buchstaben beiliegt, indem Sie auf der anderen Seite dividieren, und wir finden so seinen endgültigen Wert. Am Ende dieses Schritts haben wir das Unbekannte gelöst und wissen, welche Art von Ergebnis übrig bleibt: eine eindeutige Lösung, eine ungültige Lösung oder eine Lösung, die mit allen ganzen Zahlen zufrieden ist.
Beispiele für Gleichungen ersten Grades
Nachfolgend finden Sie gelöste Gleichungen ersten Grades , die je nach Komplexität ihrer Struktur in verschiedene Kategorien eingeteilt sind. Wenn Sie also das theoretische Verfahren zur Lösung linearer Gleichungen und die verschiedenen existierenden Typen kennen, verfügen Sie bereits über das nötige Wissen, um sie einfach lösen zu können, und wir beginnen mit der Praxis. Beginnen wir jedoch mit der theoretischen Erklärung:
Grundlegende Gleichungen ersten Grades
Diese erste Art linearer Gleichungen besteht nur aus Grundrechenarten (Addition, Subtraktion, Multiplikation und Division). Hier sind zwei ausgearbeitete Beispiele, das erste ist etwas einfacher und das zweite etwas komplexer in Bezug auf die Berechnung:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3 / 2
Gleichungen ersten Grades mit Klammern
Zweitens haben wir die linearen Gleichungen in Klammern. Diese sind etwas komplizierter zu lösen als die vorherigen, obwohl ihre einzige Schwierigkeit in der Berechnung liegt, da die Eigenschaften der Klammern beachtet werden müssen. Zur Verdeutlichung zeigen wir Ihnen zwei Praxisbeispiele:
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11 / 19
Gleichungen ersten Grades mit Potenzen und Wurzeln
Die dritte Ebene ist recht einfach, da sie nur Kräfte und Wurzeln hinzufügt. Die einzige Schwierigkeit, auf die Sie bei diesen Gleichungen stoßen können, besteht darin, dass der Exponent oder die Wurzel eine ganzzahlige Klammer beeinflusst (wie im zweiten Beispiel, das wir Ihnen zeigen), aber alles andere bleibt weitgehend gleich. Nachfolgend finden Sie zwei Beispiele.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Gleichungen ersten Grades mit Brüchen
Die letzte Kategorie linearer Gleichungen, die wir finden können, ist diese, die aus allen Elementen besteht, die wir zuvor kommentiert haben, und auch aus Brüchen. Dieses Level ist das komplexeste und es gibt mehrere Methoden, um sie zu lösen. Die erste und einfachste besteht darin, die Nenner mit der Gegenseite der Gleichheit zu multiplizieren, obwohl wir dies nur verwenden können, wenn wir zwei Brüche haben. Wenn die Gleichung hingegen mehr als zwei Brüche enthält, müssen wir einen gemeinsamen Nenner finden und alle Brüche multiplizieren, indem wir diesen Wert durch den Nenner desselben Bruchs dividieren. Nachfolgend finden Sie ein Beispiel für jeden Typ:
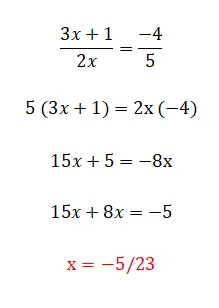
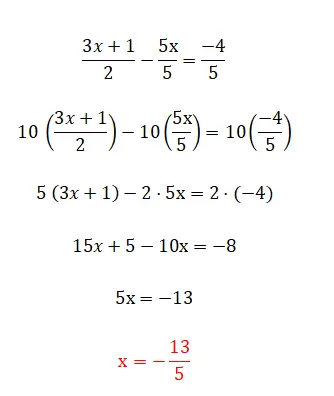
Übungen zu Gleichungen ersten Grades
Jetzt bieten wir einige Übungen zu linearen Gleichungen an. Sie sind nach steigendem Schwierigkeitsgrad geordnet, wobei die ersten Gleichungen einfacher sind als die letzten. Daher empfehlen wir Ihnen, am Anfang zu beginnen und zu sehen, wie weit Sie kommen können. Versuchen Sie also, die folgenden Gleichungen zu lösen und vergleichen Sie dann Ihr Ergebnis mit den von uns bereitgestellten Lösungen.
Erste Übung
Die erste Aufgabe ist eine sehr einfache lineare Gleichung, da sie nur aus Additionen und Subtraktionen besteht und außerdem nur vier Terme zwischen den beiden Seiten der Gleichung hat:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- Wir fassen ähnliche Begriffe zusammen.
- Wir vereinfachen beide Seiten.
- Wir löschen das Unbekannte und berechnen seinen Wert.
zweite Übung
In diesem Fall haben wir es mit einer durch Klammern gebildeten Gleichung zu tun, bei der unsere oberste Priorität darin besteht, sie zu eliminieren, damit wir dann ähnliche Begriffe zusammenfassen können:
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- Wir lösen die Klammern.
- Wir verschieben die x nach links und die unabhängigen Terme nach rechts.
- Wir klären das Unbekannte auf.
Wir vereinfachen das Ergebnis.
dritte Übung
Als nächstes müssen Sie eine weitere quadratische Gleichung mit Klammern lösen, obwohl diese etwas schwieriger ist. Dies liegt daran, dass es verschachtelte Klammern (Klammern innerhalb anderer Klammern) enthält. Deshalb müssen Sie die Reihenfolge der Lösung richtig einhalten: zuerst Insider, dann Outsider.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28 / 3
- Wir beginnen mit der Lösung der inneren Klammern.
- Als nächstes lösen wir die äußeren Klammern auf.
- Wir vereinfachen beide Seiten der Gleichheit und sammeln ähnliche Begriffe.
- Wir isolieren x und berechnen seinen Wert.
vierte Übung
In dieser Übung beginnen wir, Brüche zu erkennen, die wahrscheinlich das komplizierteste Element linearer Gleichungen sind. Aber machen Sie sich keine Sorgen, denn wenn Sie die Theorie gelesen haben, wissen Sie genau, wie es geht:
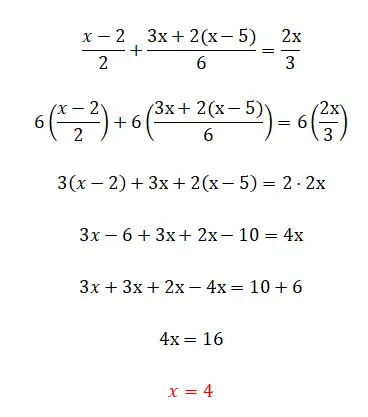
Fünfte Übung
In dieser fünften Übung sehen wir Brüche in Klammern, was bedeutet, dass die Lösungshierarchie etwas komplizierter wird. Es ist erwähnenswert, dass dieses Beispiel mit zwei Methoden gelöst werden kann: mit der Methode der kleinsten gemeinsamen Vielfachen oder durch direktes Arbeiten mit Brüchen. Unten sehen Sie die beiden vollständigen Verfahren:
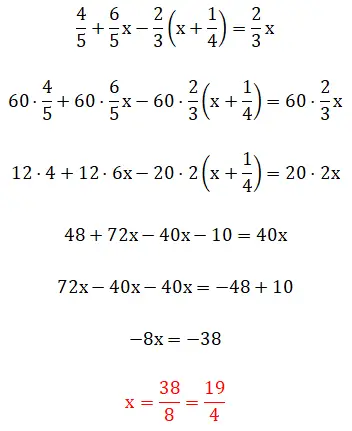
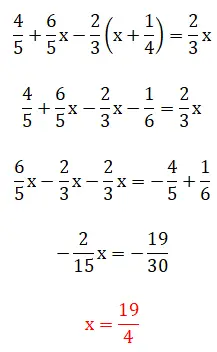
sechste Übung
Als nächstes gehen wir etwas weiter auf das Thema Brüche und Klammern ein, da wir verschachtelte Klammern haben. Diese Übung bringt im Vergleich zur vorherigen nicht viel mehr Komplikationen mit sich, sie ist einfach etwas schwieriger in Bezug auf die Berechnungen und das war’s.
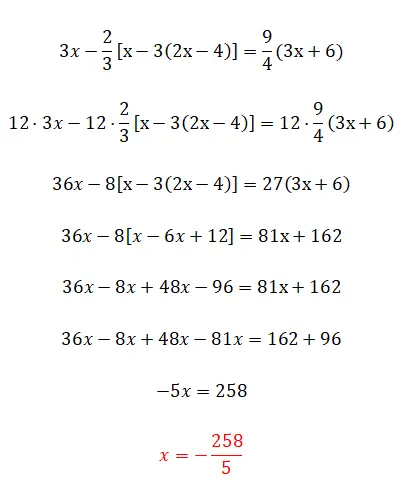
- Wir multiplizieren alle Terme mit dem LCMP der Nenner.
- Wir vereinfachen den Ausdruck, indem wir die Klammern entfernen: zuerst die inneren, dann die äußeren.
- Wir gruppieren ähnliche Begriffe auf jeder Seite.
- Wir lösen die Operationen auf jeder Seite.
- Und wir berechnen den Wert des Unbekannten.
siebte Übung
Die folgende Übung mag sehr einfach erscheinen, wir empfehlen Ihnen jedoch, sie trotzdem zu lösen, da Sie mit Sicherheit ein etwas ungewöhnliches Ergebnis erhalten. Schauen Sie sich nach dem Ausprobieren die Lösung und Erklärung unter der Übung an.
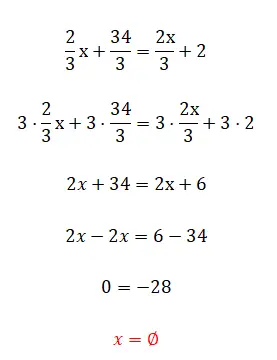
- Wir multiplizieren alle Brüche mit den lcm der Nenner.
- Wir vereinfachen den erhaltenen Ausdruck.
- Und schließlich sehen wir, dass es uns eine falsche Gleichheit gibt, da wir das Unbekannte eliminiert haben.
Wie Sie vielleicht bemerkt haben, handelt es sich hierbei um eine falsche Gleichheit oder eine Gleichheit ohne Ergebnis, da es keinen Wert gibt, der die Gleichung korrekt vervollständigt. Dies ist einer der Fälle, die wir in der Einleitung erwähnt haben.
Achte Übung
Abschließend bieten wir Ihnen diese Übung an, die ziemlich kompliziert ist, da sie alle Komplikationen aufweist, die wir in diesem Artikel gesehen haben, obwohl sie auch einen kleinen Trick enthält. Kommentieren Sie, dass Sie die gesamte Theorie perfekt verstanden haben, wenn Sie diese Gleichung ersten Grades lösen können. Und wenn nicht, machen Sie sich keine Sorgen, denn diese Übung ist ziemlich kompliziert.
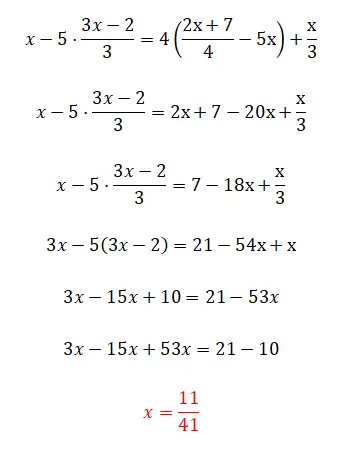
- Wir beginnen damit, die vier auf der rechten Seite der Gleichung zu eliminieren.
- Dann verbinden wir die x auf der rechten Seite.
- Wir multiplizieren alle Terme mit drei, um die Nenner zu eliminieren.
- Wir entfernen die Klammern.
- Wir haben ähnliche Begriffe zusammengestellt.
- Wir berechnen den Wert des Unbekannten.
Weitere Übungen zu linearen Gleichungen
Nachdem Sie nun genügend Übung haben, sollten Sie in der Lage sein , komplexe lineare Gleichungen zu lösen . Wenn Sie jedoch weiter üben möchten, empfehlen wir Ihnen, dieses Arbeitsblatt zu lösen. Wenn Sie jedoch der Meinung sind, dass Sie genug abgedeckt haben, können wir Ihnen auch einen Artikel anbieten, der Ihnen helfen kann, die Hierarchie der Vorgänge zu verstehen. Auf diese Weise wissen Sie jederzeit, welche Berechnung Sie zuerst lösen müssen, und machen nie einen Fehler .