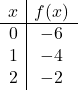Absolutwertfunktionen -

Auf dieser Seite wird erklärt, was eine Absolutwertfunktion ist. Außerdem erfahren Sie, wie Sie eine stückweise Absolutwertfunktion definieren und diese Art von Funktionen in einem Diagramm darstellen. Darüber hinaus sehen Sie es anhand von Beispielen für Absolutwertfunktionen und können mit Übungen und Schritt für Schritt gelösten Problemen üben.

Was sind absolutwertige Funktionen?

Die Definition einer Absolutwertfunktion lautet wie folgt:

Der Absolutwert einer Funktion wandelt alle ihre Bilder in positive Bilder um. Daher kann der Pfad einer absoluten Funktion niemals negative Werte haben.

Die folgende Funktion ist ein Beispiel für eine Absolutwertfunktion:

$f(x)=\lvert 5x \rvert$

Wenn wir bei der Auswertung der Funktion an einem Punkt ein positives Ergebnis erhalten, bleibt es positiv:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

Ist das Ergebnis hingegen negativ, wird es positiv:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Absolutwertfunktionen werden normalerweise in der Oberstufe gegeben, da sie aufgrund ihrer Eigenschaften etwas schwer zu verstehen sind.

So definieren Sie stückweise eine Funktion mit einem absoluten Wert

Eine absolutwertige Funktion kann als stückweise Funktion ausgedrückt werden. Dazu müssen Sie das Vorzeichen der Funktion in den Intervallen ändern, was negativ ist.

Sehen wir uns ein Beispiel an, wie man von einer Absolutwertfunktion zu einer stückweisen Funktion übergeht:

Drücken Sie die folgende Funktion mit einem Absolutwert als stückweise Funktion aus:

$f(x) = \lvert 4 - x^2 \rvert$

Als erstes müssen wir bestimmen, wann die Funktion negativ ist. Dazu setzen wir den algebraischen Ausdruck im Absolutwert gleich 0 und lösen die Gleichung:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

Wir stellen nun die erhaltenen Werte auf der Linie dar:

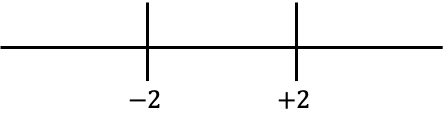
Und wir schauen uns an, welches Vorzeichen in jedem Intervall der Zeile die Funktion ohne den Absolutwert hat:

$x<-2$

Wir nehmen zum Beispiel jeden Punkt kleiner als -2

$x=-3:$

$4-(-3)^2$

$-5$

Negativ

$-2 < x < 2$

Wir nehmen zum Beispiel jeden Punkt zwischen -2 und +2

$x=0:$

$4-0^2$

$+4$

Positiv

$x>2″ title=“Rendered by QuickLaTeX.com“ height=“14″ width=“42″ style=“vertical-align: -2px;“> Wir nehmen zum Beispiel jeden Punkt, der größer als 2 ist <p class=$ $x=3:$

$4-3^2$

$-5$

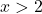
Negativ

Wie wir gesehen haben, wäre die Funktion ohne den Absolutwert auf den Intervallen negativ

$x<-2$

Und

$x>2.“ title=“Rendered by QuickLaTeX.com“ height=“14″ width=“47″ style=“vertical-align: -2px;“> Daher müssen wir die Funktion in Strichen ausdrücken, indem wir ihr Vorzeichen in diesen Intervallen ändern: 2 \end{array} \right.“ title=“Rendered by QuickLaTeX.com“ height=“97″ width=“372″ style=“vertical-align: 0px;“> 2 \end{array} \right.“ title=“Rendered by QuickLaTeX.com“ height=“97″ width=“358″ style=“vertical-align: 0px;“> Beachten Sie, dass Sie in einigen Intervallen Gleichheit berücksichtigen müssen. Hier setzen wir es zum Beispiel in das zweite Intervall <p class=$ $-2 \le x \le 2$

. Sie können es aber in jedem beliebigen Intervall platzieren, solange in allen kritischen Punkten Gleichstand herrscht. Mit anderen Worten, es wäre dasselbe, wenn wir die Funktion wie folgt definiert hätten:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

So stellen Sie eine Funktion mit einem absoluten Wert dar

Um eine Funktion mit einem Absolutwert in einem Diagramm darzustellen, müssen wir die unten beschriebenen Schritte ausführen:

Stellen Sie die Funktion so dar, als ob sie keinen absoluten Wert hätte.
Zeichnen Sie in den Intervallen, in denen die Funktion negativ ist, also unterhalb der X-Achse liegt, die symmetrische Funktion.
Löschen Sie den Teil der Funktion, der unterhalb der X-Achse liegt.

Sehen wir uns ein Beispiel an, wie eine Funktion mit einem absoluten Wert grafisch dargestellt wird

Stellen Sie die folgende Funktion als Absolutwert grafisch dar:

$f(x) = \lvert -x+2 \rvert$

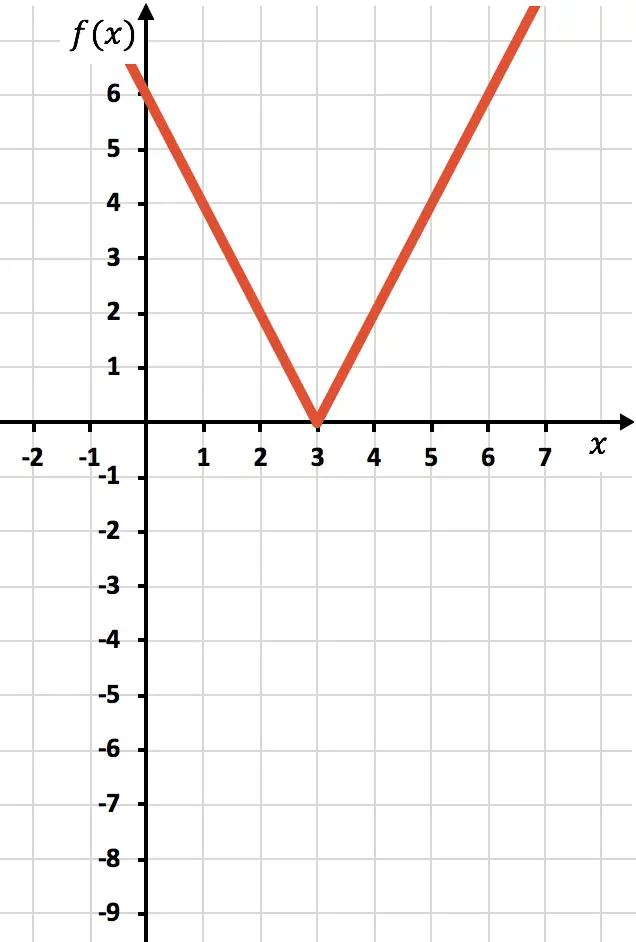
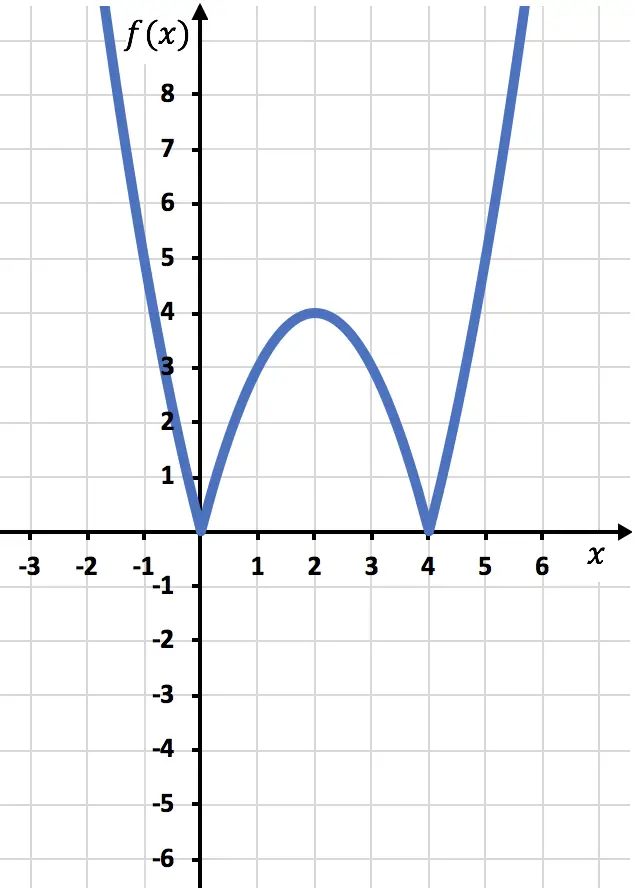
Um eine Funktion mit absolutem Wert darzustellen, müssen wir zunächst die Funktion ohne den absoluten Wert darstellen. Wir erstellen daher die Tabelle der Funktionswerte ohne den Absolutwert:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

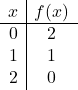
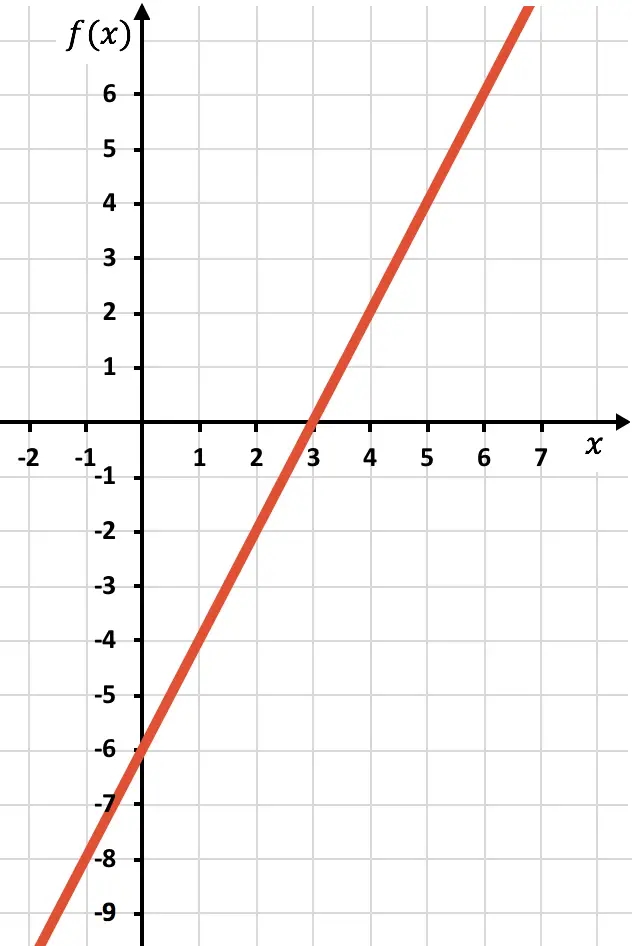
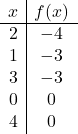
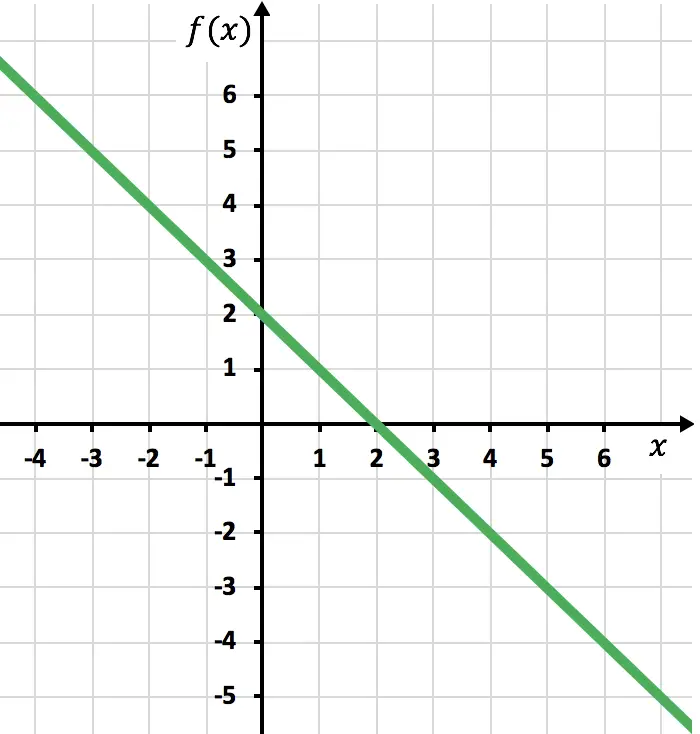
Wir zeichnen die Punkte grafisch auf und zeichnen die Linie, als wäre sie eine normale Funktion:

Wir müssen nun die symmetrische Funktion dort zeichnen, wo die Funktion negativ ist, also unterhalb der x-Achse liegt. Daher kehren wir die Funktion ausgehend von x=2 um:

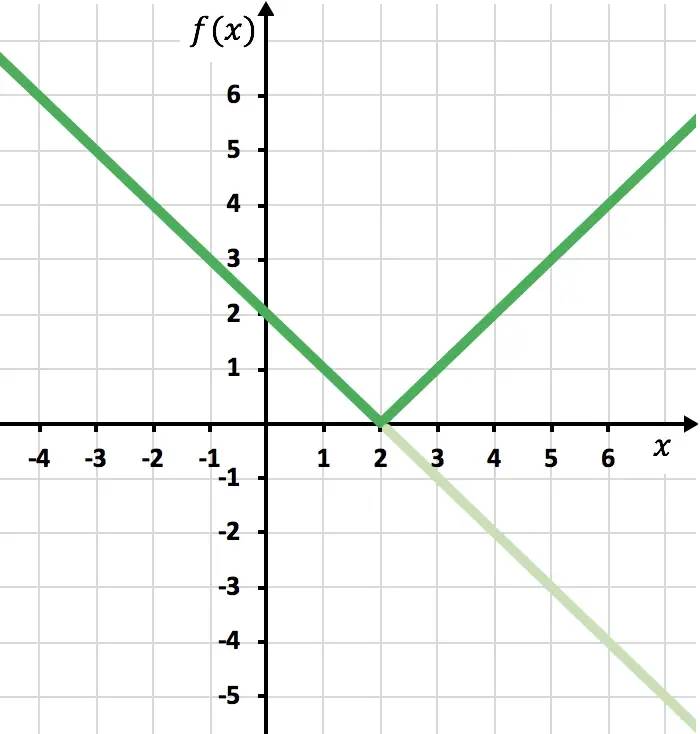
wie man eine Funktion mit einem absoluten Wert darstellt

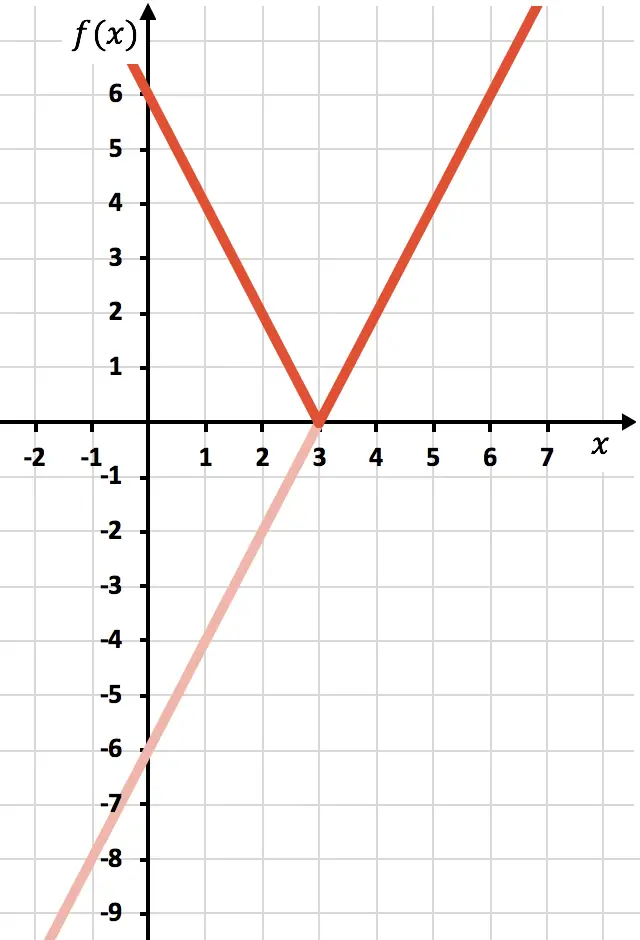
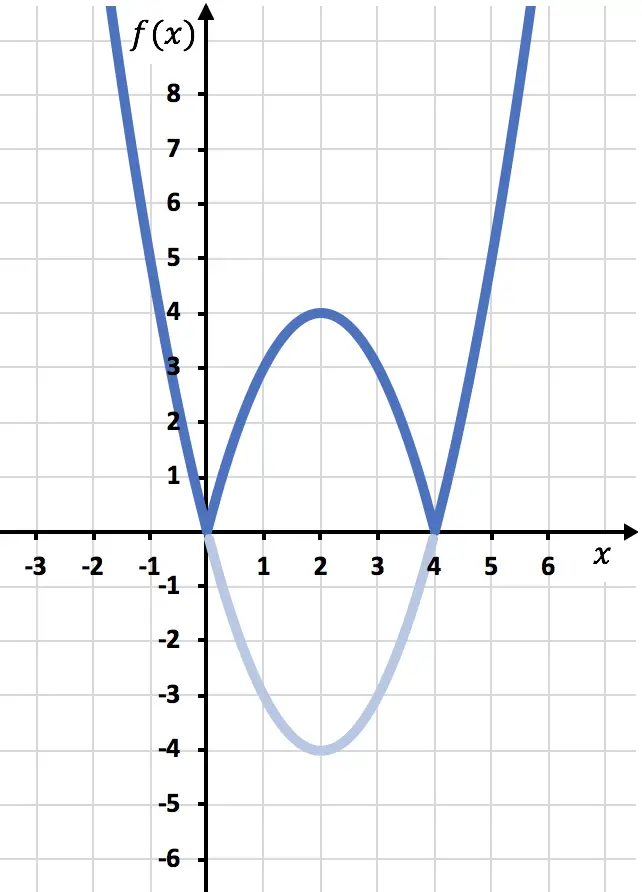
Und schließlich eliminieren wir die Spur der Funktion, die unterhalb der X-Achse liegt:

wie man eine Funktion mit einem absoluten Wert grafisch darstellt

Und damit haben wir die Funktion bereits mit einem Absolutwert dargestellt. Wie Sie gesehen haben, ändert sich lediglich, dass wir den Teil der Funktion umkehren müssen, der unterhalb der OX-Achse liegt. Daher liegt der Graph jeder Funktion mit einem Absolutwert immer auf der Seite der positiven Halb-Y-Achse.

Andererseits können wir zur Überprüfung der Konzepte aus dem Diagramm ableiten, dass der Bereich der vorherigen Absolutwertfunktion ausschließlich aus reellen Zahlen besteht. Andererseits besteht der Bereich oder Bereich der besagten Funktion mit einem Absolutwert nur aus positiven Zahlen und Nullen.

Aufgaben zu Absolutwertfunktionen gelöst

Übung 1

Drücken Sie die folgende Funktion mit einem Absolutwert als stückweise Funktion aus:

$f(x)= \lvert -x+3 \rvert$

Sehen Sie sich die Lösung an

Zunächst müssen wir uns ansehen, wann die Funktion negativ ist. Dazu setzen wir den Absolutwert gleich Null und lösen die Gleichung:

$-x+3=0$

$x=3$

Wir stellen den in der Zeile gefundenen Wert dar:

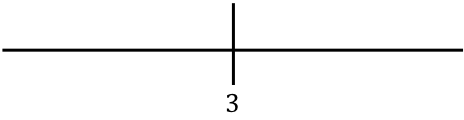
Nun werten wir einen Punkt in jedem Intervall der Funktion ohne den Absolutwert aus, um herauszufinden, welches Vorzeichen die Funktion in jedem Abschnitt der Geraden tatsächlich hat:

$x<3$

Zum Beispiel nehmen wir jeden Punkt, der kleiner als 3 ist

$x=0:$

$-0+3$

$+3$

Positiv

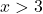$x>3″ title=“Rendered by QuickLaTeX.com“ height=“14″ width=“43″ style=“vertical-align: -2px;“> <p class=$ Zum Beispiel nehmen wir jeden Punkt, der größer als 3 ist

$x=4:$

$-4+3$

$-1$

Negativ

Die Funktion ohne den Absolutwert wäre im Intervall x>3 negativ. Wir müssen die Funktion daher in Strichen ausdrücken, indem wir ihr Vorzeichen in diesem Intervall ändern:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Übung 2

Finden Sie den stückweisen Ausdruck der folgenden Funktion mit einem absoluten Wert:

$f(x)= \lvert 3x^2-75 \rvert$

Sehen Sie sich die Lösung an

Als erstes müssen wir bestimmen, wann die Funktion negativ ist. Dazu müssen wir das Absolutwertargument gleich Null setzen und die Gleichung lösen:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

Wir stellen nun die Wurzeln der rechts erhaltenen Funktion dar:

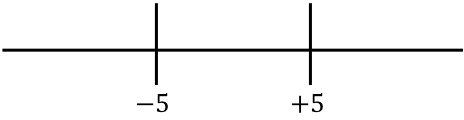
Und wir schauen uns an, welches Vorzeichen in jedem Intervall der Zeile die Funktion ohne den Absolutwert hat:

$x<-5$

Zum Beispiel nehmen wir jeden Punkt unter -5

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Positiv

$-5 < x < 5$

Wir nehmen zum Beispiel jeden Punkt zwischen -5 und +5

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

Negativ

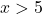$x>5″ title=“Rendered by QuickLaTeX.com“ height=“15″ width=“42″ style=“vertical-align: -2px;“> <p class=$ Zum Beispiel nehmen wir jeden Punkt, der größer als 5 ist

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

Positiv

Daher wäre die Funktion ohne den Absolutwert nur im Intervall -5<x<5 negativ. Daher müssen wir die Funktion in Teilen ausdrücken, indem wir nur das Vorzeichen dieses Intervalls ändern:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.“ title=“Rendered by QuickLaTeX.com“ height=“97″ width=“408″ style=“vertical-align: 0px;“> 5 \end{array} \right.“ title=“Rendered by QuickLaTeX.com“ height=“97″ width=“394″ style=“vertical-align: 0px;“> <div class=$

Übung 3

Um eine Funktion mit einem absoluten Wert darzustellen, müssen Sie zunächst die Funktion ohne den absoluten Wert darstellen:

Da es sich um eine affine Funktion handelt, müssen Sie eine Wertetabelle erstellen, um sie grafisch darzustellen:

Wir müssen nun die symmetrische Funktion dort zeichnen, wo die Funktion negativ ist, also unterhalb der X-Achse liegt. Daher invertieren wir die Funktion von x=3 rückwärts:

Und schließlich eliminieren wir den Teil der Funktion, der unterhalb der X-Achse liegt:

Übung 4

Um eine Funktion mit einem absoluten Wert darzustellen, müssen wir zunächst die Funktion ohne den absoluten Wert zeichnen.

Dies ist eine quadratische Funktion. Um es darzustellen, müssen wir daher die X-Koordinate des Scheitelpunkts der Parabel mit der folgenden Formel berechnen:

Wir müssen nun die Funktion symmetrisch dorthin übersetzen, wo sie negativ ist, also dort, wo sie unterhalb der OX-Achse liegt. Daher kehren wir die Funktion von x=0 auf x=4 um:

Und schließlich löschen wir den Teil der Funktion, der unterhalb der X-Achse liegt: