▷ Alles über analytische Geometrie im Raum ✅

Auf dieser Seite finden Sie die Erklärung aller Dinge über die analytische Geometrie im Raum (und die Formeln): die Gleichungen der Linie und der Ebene, die relativen Positionen zwischen Ebenen und Linien, wie Abstände und Winkel im Raum berechnet werden, …

Was ist Geometrie im Raum?

Die Raumgeometrie ist der Zweig der Geometrie, der sich mit der Untersuchung dreidimensionaler (3D) geometrischer Figuren befasst, also solcher, die einen Platz im Raum einnehmen. Wie der Kegel, der Würfel, die Pyramide, die Kugel, der Zylinder, die Prismen, die Polyeder usw.

Auf dieser Seite konzentrieren wir uns jedoch auf die analytische Geometrie im Raum , den Teil der Raumgeometrie, der sich auf die Analyse von Punkten, Linien, Ebenen, den Abständen zwischen zwei geometrischen Figuren, den Winkeln, die sie bilden, und den Schnittpunkten zwischen verschiedenen Geometrien konzentriert Figuren. Elemente usw.

Gleichungen der Linie im Raum

Denken Sie daran, dass die mathematische Definition einer Linie eine Menge aufeinanderfolgender Punkte ist, die in derselben Richtung ohne Kurven oder Winkel dargestellt werden.

Um also jede Linie in einem dreidimensionalen Raum (in R3) mathematisch auszudrücken, verwenden wir die Gleichungen der Linie, und um sie zu finden, brauchen wir nur einen Punkt, der zur Linie gehört, und den Richtungsvektor dieser Linie.

Mit nur diesen beiden geometrischen Elementen können Sie absolut alle verschiedenen Gleichungen der Geraden finden, die wie folgt lauten:

Die Gleichungen der Geraden sind die Vektorgleichung , die parametrischen Gleichungen , die kontinuierliche Gleichung und die implizite (oder allgemeine) Gleichung .

Nachfolgend finden Sie eine Erläuterung der verschiedenen Arten von Geradengleichungen.

Vektorgleichung einer Linie im Raum

$\vv{\text{v}}$

ist der Richtungsvektor der Geraden und

$P$

ein Punkt, der nach rechts gehört:

$\vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z) \qquad P(P_x,P_y,P_z)$

Die Formel für die Vektorgleichung der Geraden lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=(P_x,P_y,P_z)+t\cdot (\text{v}_x,\text{v}_y,\text{v}_z) \end{empheq}$

Parametrische Gleichungen der Linie im Raum

Wir können die Formel für die parametrische Gleichung einer Linie aus ihrer Vektorgleichung erhalten, indem wir Komponente für Komponente gleichsetzen:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_x+t\cdot\text{v}_x \\[1.7ex] y=P_y+t\cdot\text{v}_y \\[1.7ex] z=P_z+t\cdot\text{v}_z\end{cases} \end{empheq}$

Kontinuierliche Gleichung der Linie im Raum

Die Formel für die kontinuierliche Geradengleichung lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_x}{\text{v}_x}=\cfrac{y-P_y}{\text{v}_y}= \cfrac{z-P_z}{\text{v}_z} \end{empheq}$

Diese Art von Geradengleichung kann auch aus parametrischen Gleichungen erhalten werden. Die Demonstration der kontinuierlichen Gleichung finden Sie auf unserer Seite. Darüber hinaus können Sie rechts Beispiele und Übungen mit gelösten Gleichungsübungen sehen.

Allgemeine (oder implizite) Gleichungen der Linie im Raum

Schließlich erhalten wir durch Multiplikation der Brüche der stetigen Geradengleichung zwei mit zwei die allgemeinen (oder impliziten) Gleichungen der Geraden :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} A_1x+B_1y+C_1z+D_1=0 \\[1.7ex] A_2x+B_2y+C_2z+D_2=0\end{cases} \end{empheq}$

Diese Art der Geradengleichung wird auch kartesische Gleichung genannt.

Wir haben gerade die 4 wichtigsten Gleichungen der Geraden gesehen (vektorielle, parametrische, kontinuierliche und allgemeine Gleichung), es gibt jedoch noch eine weitere, etwas besondere Gleichung, deren Erklärung daher eine ganze Seite in Anspruch nimmt. Dies ist die kanonische Gleichung . In diesem Link können Sie ihre gesamte Erklärung sehen, warum sie so besonders ist und was sie von allen anderen unterscheidet.

Ebenengleichungen im Raum

In der analytischen Geometrie ist die Gleichung einer Ebene eine Gleichung, die es ermöglicht, jede Ebene analytisch auszudrücken. Um die Gleichung einer Ebene zu finden, benötigen Sie also nur einen Punkt und zwei linear unabhängige Vektoren, die zu dieser Ebene gehören.

Somit sind alle Arten von Gleichungen der Ebene: die Vektorgleichung , die parametrischen Gleichungen , die implizite (oder allgemeine) Gleichung und die kanonische (oder segmentale) Gleichung der Ebene.

Als nächstes sehen wir die Erklärung und Formel aller Gleichungen des Plans.

Vektorgleichung der Ebene

Gegeben sei ein Punkt und zwei Richtungsvektoren einer Ebene:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Die Formel für die Vektorgleichung einer Ebene lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

Oder gleichwertig:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Gold

$\lambda$

Und

$\mu$

Es handelt sich um zwei Skalare, also zwei reelle Zahlen.

Parametrische Gleichungen der Ebene

Andererseits lautet die Formel für die parametrische Gleichung der Ebene :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Implizite oder allgemeine Gleichung der Ebene

Die implizite Gleichung eines Plans, auch allgemeine Gleichung genannt, erhält man, indem man die folgende Determinante löst und das Ergebnis auf 0 setzt:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Somit hat die implizite oder allgemeine Gleichung des resultierenden Plans die folgende Form:

Diese Art von Ebenengleichung wird auch als kartesische Ebenengleichung bezeichnet.

Kanonische oder segmentale Gleichung der Ebene

Die Formel für die kanonische oder segmentale Gleichung einer Ebene lautet wie folgt:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Gold:

$a$

Dies ist der Schnittpunkt zwischen der Ebene und der X-Achse.
$b$

Dies ist der Schnittpunkt zwischen der Ebene und der Y-Achse.
$c$

Hier schneidet die Ebene die Z-Achse.

Vektor normal zu einer Ebene

Der Normalenvektor zu einer Ebene ist ein Vektor senkrecht zu allen in dieser Ebene enthaltenen Linien. Daher bedeutet ein Vektor normal zu einer Ebene, dass er senkrecht zur Ebene steht.

Viele metrische Probleme in der räumlichen analytischen Geometrie betreffen Ebenen und ihre Normalenvektoren. Um diese Aufgaben zu lösen, müssen Sie lediglich die mathematische Beziehung zwischen einer Ebene und ihrem Normalenvektor kennen:

Die Komponenten X, Y, Z des Vektors senkrecht zu einer Ebene stimmen jeweils mit den Koeffizienten A, B, C der impliziten (oder allgemeinen) Gleichung dieser Ebene überein.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Gold

$\vv{n}$

ist der Vektor orthogonal zur Ebene

$\pi.$

Relative Positionen zweier geometrischer Elemente im Raum

Offensichtlich muss eine Linie oder eine Ebene nicht unbedingt allein im Raum sein, im Gegenteil, sie interagieren normalerweise miteinander: Sie schneiden sich, sind parallel, senkrecht usw. Nun, in diesem Abschnitt werden wir die unterschiedlichen relativen Positionen von Linien und Ebenen sehen und wie sie bestimmt werden.

Relative Position zweier Linien im Raum

In der analytischen Geometrie gibt es beim Arbeiten in einem dreidimensionalen Raum (in R3) 4 mögliche relative Positionen zwischen zwei Linien: Zwei Linien können zusammenfallende Linien , parallele Linien , Sekantenlinien oder Sekantenlinien sein.

Parallele Linien

relative Position zweier paralleler Linien

Zwei Geraden sind parallel, wenn sie die gleiche Richtung haben, aber keinen gemeinsamen Punkt haben. Außerdem haben parallele Linien immer den gleichen Abstand voneinander.

Zusammenfallende Linien

relative Position zweier zusammenfallender Linien

Zwei Geraden fallen zusammen, wenn sie die gleiche Richtung haben und alle ihre Punkte gemeinsam sind.

Schnittlinien

Zwei sich schneidende Linien haben unterschiedliche Richtungen, berühren sich aber an einem Punkt.

Schnittlinien

Zwei sich schneidende Linien haben unterschiedliche Richtungen und schneiden sich an keinem Punkt. Zwei gekreuzte Linien liegen also nicht in derselben Ebene. Beispielsweise in der grafischen Darstellung oberhalb der Linie

$s$

liegt immer vor der Geraden

$r$

, sodass sie sich niemals berühren werden.

So ermitteln Sie die relative Position zweier Linien anhand von Bereichen

Eine Möglichkeit, die relative Position zweier Zeilen zu ermitteln, besteht darin, die Bereiche zweier spezifischer Matrizen zu berechnen, wie wir weiter unten sehen werden. Diese Methode ist sehr nützlich, wenn die beiden Linien in Form einer impliziten (oder allgemeinen) Gleichung ausgedrückt werden.

Wenn wir also zwei Linien haben, die mit ihren impliziten (oder allgemeinen) Gleichungen in einem dreidimensionalen Raum (in R3) ausgedrückt werden:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Sei A die Matrix, die sich aus den Koeffizienten der beiden Geraden zusammensetzt:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

Und gegeben ist die erweiterte Matrix A‘, die aus allen Parametern der beiden Linien gebildet wird:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Dann kann die relative Position der beiden Linien anhand der Ausdehnung der beiden vorherigen Matrizen gemäß der folgenden Tabelle bestimmt werden:

relative Positionen zweier Linien nach Bereichen

Um die relative Position zwischen zwei Zeilen zu ermitteln, müssen wir daher die Bereiche beider Matrizen berechnen, und je nach Bereich jeder Matrix wird es den einen oder anderen Fall geben.

Dieser Satz kann mit dem Satz von Rouché-Frobenius (einer Methode zur Lösung linearer Gleichungssysteme) bewiesen werden. Auf dieser Seite werden wir den Beweis jedoch nicht durchführen, da er recht umständlich ist und nicht viel hinzufügt. .

Relative Lage zweier Ebenen im Raum

In der analytischen Geometrie gibt es nur drei mögliche relative Positionen zwischen zwei Ebenen: sich schneidende Ebenen, parallele Ebenen und zusammenfallende Ebenen.

Sich schneidende Ebenen : Zwei Ebenen schneiden sich, wenn sie sich nur auf einer Linie schneiden.
Parallele Ebenen : Zwei Ebenen sind parallel, wenn sie sich in keinem Punkt schneiden.
Zusammenfallende Ebenen : Zwei Ebenen sind zusammenfallend, wenn sie alle Punkte gemeinsam haben.

Sich überschneidende Aufnahmen

relative Lage zweier sich schneidender Ebenen

parallele Ebenen

Passende Pläne

relative Lage zweier zusammenfallender Ebenen

So bestimmen Sie die relative Position zweier Ebenen anhand von Koeffizienten

Eine Möglichkeit, die relative Position zwischen zwei Ebenen zu ermitteln, besteht darin, die Koeffizienten ihrer allgemeinen (oder impliziten) Gleichungen zu verwenden.

Betrachten Sie dann die allgemeine (oder implizite) Gleichung zweier verschiedener Ebenen:

$\pi_1 : \ Ax+By+Cz+D=0$

$\pi_2 : \ A'x+B'y+C'z+D'=0$

Die relative Position zwischen den beiden Ebenen in einem dreidimensionalen Raum hängt von der Proportionalität ihrer Koeffizienten oder Parameter ab:

relative Position zweier Ebenen mit Parametern

Somit schneiden sich die beiden Ebenen, wenn einer der Koeffizienten A, B oder C nicht proportional zu den anderen ist. Andererseits sind die beiden Ebenen parallel, wenn nur die unabhängigen Terme nicht proportional sind. Und schließlich stimmen die Pläne überein, wenn alle Koeffizienten der beiden Gleichungen proportional sind.

Entfernungen im Raum

Nachfolgend finden Sie die Formeln zur Berechnung des Abstands zwischen verschiedenen geometrischen Elementen: zwischen einem Punkt und einer Linie, zwischen zwei Ebenen, zwischen einer Ebene und einer Linie, …

Abstand zwischen zwei Punkten

Der Abstand zwischen zwei Punkten entspricht der Norm des durch diese beiden Punkte bestimmten Vektors.

Wenn wir also zwei allgemeine Punkte haben:

$A(a_x,a_y,a_z) \qquad \qquad B(b_x,b_y,b_z)$

Die Formel für den Abstand zwischen den beiden Punkten lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(A,B) = \vert \vv{AB} \rvert = \sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2} \end{empheq}$

Abstand von einem Punkt zu einer Linie

Die Formel zur Berechnung des Abstands von einem Punkt zu einer Linie im Raum lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert} \end{empheq}$

Gold:

$\lvert \vv{\text{v}}_r \rvert$

ist der Modul des Richtungsvektors der Linie

$r.$
$Q$

ist ein Punkt auf der rechten Seite

$r,$

$P$

ein Punkt auf der Linie

$s$

Und

$\vv{QP}$

der durch die beiden Punkte definierte Vektor
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

ist der Modul des Vektorprodukts zwischen den Vektoren

$\vv{QP}$

Und

$\vv{\text{v}}_r$

Abstand zwischen zwei Linien

Der Abstand zwischen zwei Linien hängt von ihrer relativen Position ab:

Wenn die beiden Geraden zusammenfallen oder sich schneiden , ist der Abstand zwischen den beiden Geraden gleich Null, da sie sich (mindestens) in einem Punkt schneiden.
Wenn die beiden Geraden parallel sind oder sich schneiden, muss je nach Fall eine Formel angewendet werden (beide Erklärungen finden Sie weiter unten).

Abstand zwischen zwei parallelen Linien

Zwei parallele Linien haben immer den gleichen Abstand voneinander. Um also den Abstand zwischen zwei parallelen Linien im Raum (in R3) zu berechnen, geschieht dies auf die gleiche Weise wie in der Ebene (in R2): Sie müssen nur einen Punkt auf einer der beiden Linien nehmen und dort den Abstand ermitteln Dies ist von diesem Punkt zur anderen Linie.

Um also den Abstand zwischen zwei parallelen Linien zu bestimmen, müssen Sie die Formel für den Abstand zwischen einem Punkt und einer Linie verwenden.

Abstand zwischen zwei sich schneidenden Linien

Der Richtungsvektor und ein beliebiger Punkt zweier Schnittlinien seien:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

Die Formel für den Abstand zwischen zwei sich schneidenden Geraden lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} \end{empheq}$

Gold:

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

ist der Absolutwert des gemischten Produkts der Vektoren

$\vv{\text{u}}, \vv{\text{v}}$

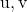
und der durch die Punkte definierte Vektor

$A$

Und

$B$

.
$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

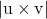
ist der Modul des Vektorprodukts zwischen den Richtungsvektoren der beiden gekreuzten Linien.

Obwohl Sie hier die Formel haben, ist die Bestimmung des Abstands zwischen zwei sich schneidenden Linien komplizierter als es scheint. Wenn Sie also üben möchten, finden Sie im folgenden Link Beispiele und gelöste Übungen zum Abstand zwischen zwei Schnittlinien.

Abstand von einem Punkt zu einer Ebene

Gegeben sei ein Punkt und die allgemeine (oder implizite) Gleichung einer Ebene:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

Die Formel für den Abstand von einem Punkt zu einer Ebene lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}} \end{empheq}$

Wie groß ist der Abstand von einem Punkt zu einer Ebene?

Wenn wir durch Anwendung der Formel ein Ergebnis gleich Null erhalten, bedeutet dies offensichtlich, dass der Abstand zwischen dem Punkt und der Ebene Null ist und der Punkt daher Teil dieser Ebene ist.

Abstand zwischen zwei Ebenen

Der Abstand zwischen zwei Ebenen im Raum hängt von der relativen Position zwischen diesen beiden Ebenen ab:

Wenn sich die beiden Ebenen schneiden oder zusammenfallen , ist der Abstand zwischen ihnen gleich Null, da sie sich in einem bestimmten Punkt schneiden.
Wenn die beiden Ebenen parallel sind, wird der Abstand zwischen den beiden Ebenen berechnet, indem man einen Punkt auf einer der beiden Ebenen nimmt und den Abstand zwischen diesem Punkt und der anderen Ebene berechnet.

Abstand zwischen zwei parallelen Ebenen

Zwei parallele Ebenen haben immer den gleichen Abstand voneinander. Um den Abstand zwischen zwei parallelen Ebenen zu ermitteln, können wir einen Punkt auf einer der beiden Ebenen nehmen und den Abstand von diesem Punkt zur anderen Ebene berechnen.

Um also den Abstand zwischen zwei parallelen Ebenen zu berechnen, müssen Sie einen Punkt auf einer der beiden Ebenen finden und dann die Formel für den Abstand zwischen einem Punkt und einer Ebene verwenden.

Winkel im Raum

Wie bei Entfernungen hängt auch die Bestimmung des Winkels zwischen zwei geometrischen Objekten im Raum von deren geometrischen Eigenschaften ab. Denn die Berechnung des Winkels zwischen zwei Linien ist nicht dasselbe wie die Berechnung des Winkels zwischen zwei Ebenen. Nachfolgend finden Sie die Formeln zum Ermitteln der Winkel zwischen Linien und Ebenen.

Winkel zwischen zwei Linien

Um den Winkel zwischen zwei Linien im euklidischen Raum zu kennen, müssen wir den Winkel berechnen, der durch ihre Richtungsvektoren gebildet wird, also:

Gegeben seien die Richtungsvektoren zweier verschiedener Geraden:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y,\text{u}_z)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

Der durch diese beiden Linien gebildete Winkel kann mit der folgenden Formel berechnet werden:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Gold

$\lvert \vv{\text{u}} \rvert$

Und

$\lvert \vv{\text{v}} \rvert$

sind die Module der Vektoren

$\vv{\text{u}}$

Und

$\vv{\text{v}}$

jeweils.

Denken Sie daran, dass die Formel für den Modul eines Vektors lautet:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Winkel zwischen zwei Ebenen

Der Winkel zwischen zwei Ebenen ist gleich dem Winkel, den die Normalenvektoren dieser Ebenen bilden. Um den Winkel zwischen zwei Ebenen zu ermitteln, berechnen wir daher den Winkel, den ihre Normalenvektoren bilden, da sie äquivalent sind .

Gegeben sei die allgemeine (oder implizite) Gleichung zweier verschiedener Ebenen:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

Der Normalenvektor jeder Ebene ist:

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

Und der von diesen beiden Ebenen gebildete Winkel wird bestimmt, indem der von ihren Normalenvektoren gebildete Winkel mit der folgenden Formel berechnet wird:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

Winkel zwischen einer Linie und einer Ebene

Der von einer Linie und einer Ebene gebildete Winkel ist definiert als der kleinere der beiden komplementären Winkel, die durch den Richtungsvektor der Linie und den Normalenvektor der Ebene gebildet werden.

Deshalb, wenn

$\vv{\text{v}}$

ist der Richtungsvektor der Geraden und

$\vv{n}$

ist der Vektor normal zur Ebene:

$\vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

$\vv{n}=(n_x,n_y,n_z)$

Die Formel zur Berechnung des Winkels zwischen einer Linie und einer Ebene lautet:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \text{sen}(\alpha)=\cfrac{\lvert \vv{\text{v}} \cdot \vv{n}\rvert}{\lvert \vv{\text{v}} \rvert \cdot \lvert \vv{n} \rvert} \end{empheq}$

Analytische geometrie im raum (formeln)

Was ist Geometrie im Raum?

Gleichungen der Linie im Raum

Vektorgleichung einer Linie im Raum

Parametrische Gleichungen der Linie im Raum

Kontinuierliche Gleichung der Linie im Raum

Allgemeine (oder implizite) Gleichungen der Linie im Raum

Ebenengleichungen im Raum

Vektorgleichung der Ebene

Parametrische Gleichungen der Ebene

Implizite oder allgemeine Gleichung der Ebene

Kanonische oder segmentale Gleichung der Ebene

Vektor normal zu einer Ebene

Relative Positionen zweier geometrischer Elemente im Raum

Relative Position zweier Linien im Raum

So ermitteln Sie die relative Position zweier Linien anhand von Bereichen

Relative Lage zweier Ebenen im Raum

So bestimmen Sie die relative Position zweier Ebenen anhand von Koeffizienten

Entfernungen im Raum

Abstand zwischen zwei Punkten

Abstand von einem Punkt zu einer Linie

Abstand zwischen zwei Linien

Abstand zwischen zwei parallelen Linien

Abstand zwischen zwei sich schneidenden Linien

Abstand von einem Punkt zu einer Ebene

Abstand zwischen zwei Ebenen

Abstand zwischen zwei parallelen Ebenen

Winkel im Raum

Winkel zwischen zwei Linien

Winkel zwischen zwei Ebenen

Winkel zwischen einer Linie und einer Ebene

Kommentar verfassen Kommentieren abbrechen