▷ Wie berechnet man den Mittelpunkt eines Segments? (Formel)

Auf dieser Seite wird die Bedeutung des Mittelpunkts eines Segments erläutert. Darüber hinaus erfahren Sie, wie Sie mithilfe der Formel die Mitte eines Segments ermitteln. Sie sehen sogar Beispiele, Übungen und gelöste Probleme zu Segmentmittelpunkten.

Was ist der Mittelpunkt eines Segments?

In der Mathematik ist der Mittelpunkt einer Strecke der Punkt, der im gleichen Abstand von den Endpunkten einer Strecke liegt. Die Mitte teilt das Segment also in zwei gleiche Teile.

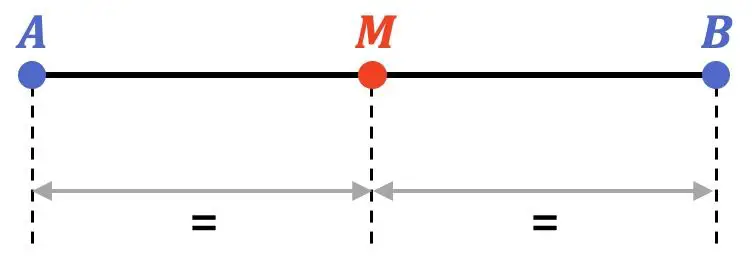
Außerdem liegt der Mittelpunkt genau in der Mitte des Segments, gehört also zur Winkelhalbierenden des Segments.

Andererseits ist der Mittelpunkt eines Segments auch ein Punkt, der von zwei geometrischen Elementen gleich weit entfernt ist: den beiden Enden des Segments.

Wie berechnet man den Mittelpunkt eines Segments?

Gegeben sind die kartesischen Koordinaten der Extrempunkte eines Segments:

$A(x_1,y_1) \qquad B(x_2,y_2)$

Die Koordinaten der Mitte dieses Segments entsprechen der Halbsumme der Koordinaten der Extrempunkte:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

Dies ist die Formel für die Mitte eines Segments in der kartesischen Ebene (im R2). Aber offensichtlich ist die Formel auch auf den kartesischen Raum (im R3) anwendbar, Sie müssen nur die Halbsumme der Z-Koordinate addieren:

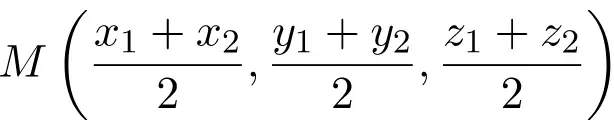
Schauen wir uns ein Beispiel für die Berechnung der Koordinaten des Mittelpunkts eines Segments an:

Bestimmen Sie den Mittelpunkt des Segments, das aus den folgenden Punkten besteht:

$A(2,5) \qquad B(4,-1)$

Um die Mitte des Segments zu finden, wenden Sie einfach die Formel an:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

Übungen, die in der Mitte eines Segments gelöst werden

Übung 1

Was ist der Mittelpunkt des Segments, dessen Endpunkte die folgenden zwei Punkte sind?

$A(3,-2) \qquad B(5,8)$

Sehen Sie sich die Lösung an

Um die Mitte des Segments zu finden, müssen Sie die Formel direkt anwenden:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

Übung 2

Finden Sie die Koordinaten des Endpunkts des Segments, das bei Punkt A beginnt und dessen Mittelpunkt M ist.

$A(4,-1) \qquad M(-2,1)$

Sehen Sie sich die Lösung an

In diesem Fall kennen wir die Koordinaten des Anfangspunkts und der Mitte des Segments. Deshalb setzen wir die uns bekannten Koordinaten in die Formel für den Mittelpunkt eines Segments ein:

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

Und nun ermitteln wir die Koordinaten des Endpunkts des Segments aus der vorherigen Gleichung:

X-Koordinaten

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

Y-Koordinaten

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

Die Koordinaten des endgültigen Endes des Segments lauten daher:

$\bm{B(-8,3)}$

Übung 3

Gegeben sei das folgende Parallelogramm:

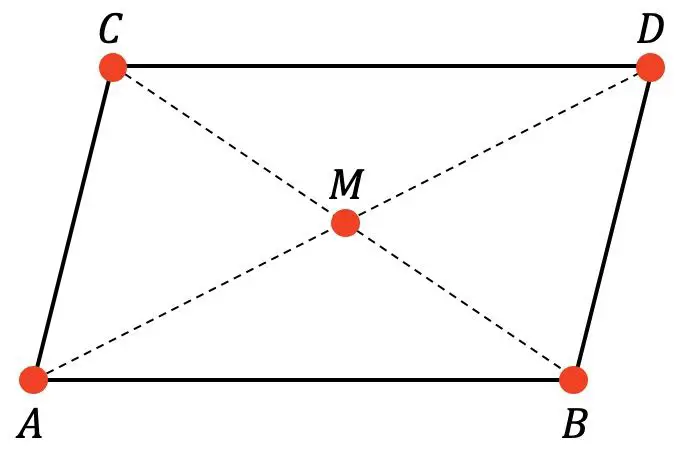
Wir wissen, dass M der Mittelpunkt des Parallelogramms ist und die Koordinaten der Punkte A, B und C sind:

$A(1,1) \quad B(5,1) \quad C(7,3)$

Berechnen Sie anhand dieser Informationen und unter Verwendung der Mittelpunktsformel die Koordinaten von Punkt D.

Sehen Sie sich die Lösung an

Um die Koordinaten von Punkt D mithilfe der Formel für die Mitte eines Segments zu ermitteln, müssen Sie zunächst die Koordinaten von Punkt M und dann die von Punkt D berechnen.

Punkt M ist der Mittelpunkt des Segments BC, seine Koordinaten sind daher:

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

Und sobald wir Punkt M kennen, können wir Punkt D finden. Punkt M ist auch die Mitte des Segments AD, also:

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

X-Koordinate von Punkt D

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

Y-Koordinate von Punkt D

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

Die Koordinaten von Punkt D sind daher:

$\bm{D(11,3}$

Übung 4

Berechnen Sie die stetige Gleichung der Geraden senkrecht zum Segment PQ in seinem Mittelpunkt. Seien Sie die Punkte

$P(1,4)$

Und

$Q(5,-2).$

Sehen Sie sich die Lösung an

Um die Gleichung einer Geraden zu bestimmen, benötigen wir ihren Richtungsvektor und einen Punkt, der Teil der Geraden ist.

In diesem Fall steht der Richtungsvektor der Linie senkrecht zum Vektor

$\vv{PQ}.$

Wir berechnen daher den Vektor

$\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

Und wir können einen Vektor senkrecht zu einem anderen finden , indem wir die Komponenten des Vektors zwischen ihnen ändern und dann das Vorzeichen einer Komponente ändern, also:

$\vv{PQ}_\perp =(6,4)$

Da wir nun den Richtungsvektor der Geraden haben, benötigen wir nur noch einen zur Geraden gehörenden Punkt. In diesem Fall sagt uns die Anweisung, dass die Linie durch den Mittelpunkt des Segments verläuft, also berechnen wir den Mittelpunkt mit der Formel:

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

Schließlich konstruieren wir die kontinuierliche Gleichung der Geraden aus dem berechneten Punkt und Vektor:

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

Formel für die mitte eines segments

Was ist der Mittelpunkt eines Segments?

Wie berechnet man den Mittelpunkt eines Segments?

Übungen, die in der Mitte eines Segments gelöst werden

Übung 1

Übung 2

Übung 3

Übung 4

Kommentar verfassen Kommentieren abbrechen