Auf dieser Seite erfahren Sie, wie Sie den Abstand zwischen zwei Punkten in der Geometrie berechnen (Formel). Sie können sich auch Beispiele ansehen und zusätzlich mit gelösten Übungen den Abstand zwischen zwei Punkten üben.
Wie lautet die Formel für den Abstand zwischen zwei Punkten?
Der Abstand zwischen zwei Punkten ist gleich der Länge des sie verbindenden Segments. Um in der Mathematik den Abstand zwischen zwei verschiedenen Punkten zu bestimmen, müssen wir daher die Quadrate der Differenzen zwischen ihren Koordinaten berechnen und dann die Wurzel der Summe dieser Quadrate ermitteln.
Mit anderen Worten lautet die Formel zur Berechnung des Abstands zwischen zwei verschiedenen Punkten auf der kartesischen Ebene wie folgt:
Betrachten Sie die Koordinaten zweier unterschiedlicher Punkte:
![]()
Die Formel für den Abstand zwischen zwei Punkten lautet:
![]()
Diese Formel ergibt sich aus der Größe eines Vektors. Tatsächlich berechnen wir mit dieser Formel die Größe des Vektors, der durch die beiden fraglichen Punkte bestimmt wird. Weitere Informationen hierzu finden Sie in der Erklärung zum Modul eines Vektors .
Andererseits kann in der analytischen Geometrie der Nachweis der Formel für den Abstand zwischen zwei Punkten auch mit dem Satz des Pythagoras erfolgen:
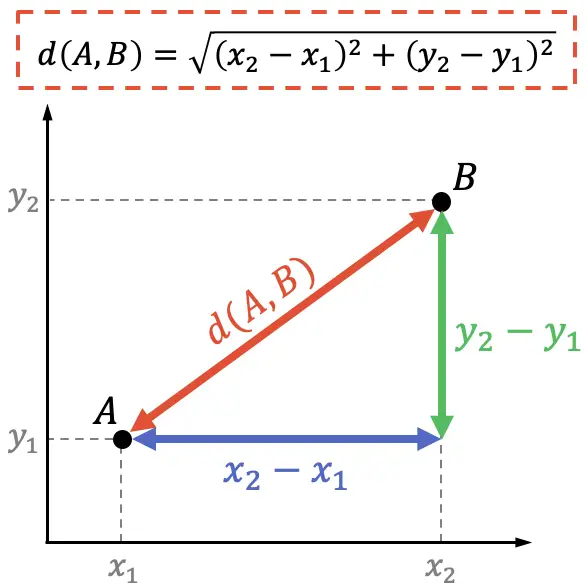
Der Satz des Pythagoras besagt, dass das Quadrat der Hypotenuse eines rechtwinkligen Dreiecks der Summe der Quadrate seiner Schenkel entspricht, daher:
![]()
Und um die Formel zu erhalten, müssen Sie nur den Abstand zwischen den beiden Punkten ermitteln:
![]()
Abschließend ist es erwähnenswert, dass, wenn wir mit 3-Koordinatenpunkten arbeiten würden, die Formel für den Abstand zwischen zwei Punkten im Raum (in R3) dieselbe wäre, aber unter Hinzufügung der Z-Koordinate:
![]()
Beispiel für die Berechnung des Abstands zwischen zwei Punkten
Nachdem wir die Definition der Formel für den Abstand zwischen zwei Punkten gesehen haben, sehen wir uns nun anhand eines Beispiels an, wie man diesen Abstand ermittelt:
- Finden Sie den Abstand zwischen den folgenden zwei Punkten:
![]()
Um den Abstand zwischen den beiden Punkten geometrisch zu ermitteln, wenden Sie einfach die Formel an:
![]()
Jetzt setzen wir die Koordinaten der Punkte in die Formel ein:
![]()
Und wir machen die Berechnungen:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e48600907e65f89fb9be0d55a2d3b3a_l3.png)
Der Abstand zwischen den beiden Punkten beträgt daher 5 Einheiten.
Offensichtlich muss uns der Distanzwert immer ein positives Vorzeichen geben, denn Distanzen sind immer positiv. Andernfalls bedeutet dies, dass wir bei einem Schritt einen Fehler gemacht haben.
Fehlerbehebung Abstand zwischen zwei Punkten
Übung 1
Berechnen Sie den Abstand zwischen den folgenden zwei Punkten:
![]()
Um den geometrischen Abstand zwischen den beiden Punkten zu ermitteln, verwenden Sie einfach die Formel:
![]()
Jetzt setzen wir die Koordinaten der Punkte in die Formel ein:
![]()
Und wir machen die Berechnungen:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81d70676cabdc2985f2ebe7b88c54e2d_l3.png)
Übung 2
Finden Sie den Abstand zwischen den folgenden zwei Punkten:
![]()
Um den mathematischen Abstand zwischen den beiden Punkten zu ermitteln, müssen wir die entsprechende Formel verwenden:
![]()
Jetzt setzen wir die Koordinaten der Punkte in die Formel ein:
![]()
Und wir machen die Berechnungen:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c9f9f5c93377868a352891d5b09630a_l3.png)
Übung 3
Berechnen Sie den Umfang des Dreiecks, das durch die Punkte A, B und C gebildet wird, wie unten grafisch dargestellt:
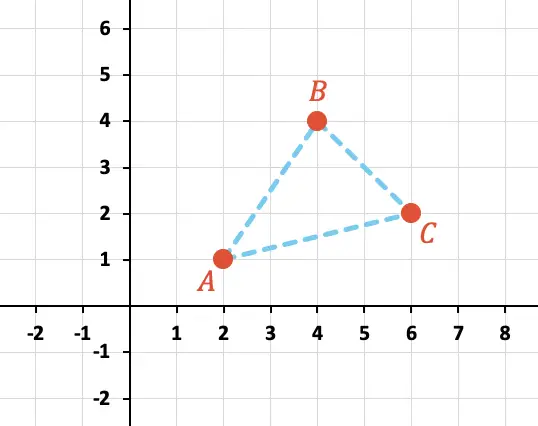
Zuerst müssen wir die X- und Y-Koordinaten jedes Punktes im Diagramm identifizieren:
![]()
![]()
![]()
Und jetzt müssen wir den Abstand zwischen allen Punkten mit der Formel berechnen:
![]()
![]()
![]()
Der Umfang des Dreiecks ist also die Summe der Längen der drei Seiten:
![]()
Übung 4
Überprüfen Sie, ob das Dreieck, dessen Eckpunkte die Punkte A, B und C sind, ein gleichschenkliges Dreieck ist. Aber die drei Punkte:
![]()
Damit ein Dreieck gleichschenklig ist, müssen zwei seiner Seiten gleich sein. Wir müssen daher die Länge jeder seiner Seiten ermitteln, die den Abständen zwischen seinen Eckpunkten entspricht.
Wir berechnen daher den Abstand zwischen den Eckpunkten des Dreiecks:
![]()
![]()
![]()
Das Dreieck hat also zwei identische Seiten und die dritte Seite misst anders als die anderen beiden, dann handelt es sich praktisch um ein gleichschenkliges Dreieck.
Übung 5
Suchen Sie einen Punkt auf der Y-Achse, der von den folgenden zwei Punkten gleich weit entfernt ist:
![]()
Wenn sich der Punkt zunächst auf der Computerachse (OY-Achse) befindet, bedeutet dies, dass die Abszisse des Punktes Null ist:
![]()
Zweitens: Wenn der Punkt den gleichen Abstand von den Punkten A und B hat, bedeutet dies, dass die folgende Gleichung erfüllt ist:
![]()
Wenn wir also die Formel für den Abstand zwischen zwei Punkten verwenden, können wir den Wert der Variablen y aus der vorherigen Gleichung ermitteln:
![]()
Da beide Seiten der Gleichung eine Wurzel haben, können wir sie vereinfachen:
![]()
Wir lösen die bemerkenswerten Potenzen und Gleichungen (oder bemerkenswerten Produkte):
![]()
Und wir operieren, bis wir den Wert des unbekannten y finden:
![]()
![]()
![]()
![]()
Kurz gesagt, der Punkt, nach dem uns die Problemstellung fragte, ist:
![]()
Wenn Sie diesen Artikel nützlich fanden, werden Sie wahrscheinlich auch an Übungen zum Abstand zwischen einem Punkt und einer Linie interessiert sein. Auf der verlinkten Seite finden Sie nicht nur Schritt für Schritt gelöste Übungen, sondern auch eine ausführliche Erklärung zur Berechnung des Abstands zwischen Punkten und Linien, Beispiele und die Anwendung der Formel für den Abstand zwischen einem Punkt und einer Linie, um eine andere Art von Abstand zu ermitteln .