So faktorisieren sie polynome (polynomfaktorisieren)

Auf dieser Seite erklären wir, wie man jede Art von Polynom faktorisiert. Wir werden zunächst sehen, wie man ein Polynom mit der Ruffini-Regel faktorisiert, dann werden wir damit fortfahren, wie Polynome ohne unabhängigen Term faktorisiert werden, dann werden wir die Faktorisierungen von Wurzelpolynomen mit Brüchen analysieren und schließlich die Sonderfälle von Faktorisierungen (bemerkenswert). Identitäten, Faktorisierung durch Gruppierung, Trinome usw.). Alle Erklärungen erfolgen anhand von Beispielen und am Ende haben Sie außerdem die Möglichkeit, mit den Schritt für Schritt gelösten Übungen die Faktorisierung von Polynomen zu üben.

Was ist Polynomfaktorisierung?

Polynomfaktorisierung ist eine Technik, die in der Mathematik verwendet wird, um ein Polynom in das Produkt von Faktoren zu zerlegen.

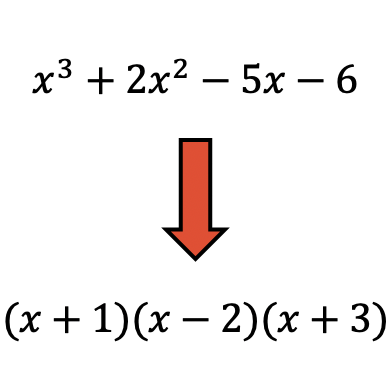
Das Faktorisieren von Polynomen ist sehr nützlich, da es einfacher ist, Operationen mit faktorisierten Polynomen durchzuführen.

Nachdem wir nun wissen, was Polynomfaktorisierung ist, sehen wir uns an, wie Polynome faktorisiert werden.

Wie man Polynome mit der Ruffini-Regel faktorisiert

Um zu verstehen, wie man ein Polynom mit der Ruffini-Regel faktorisiert, muss man natürlich zunächst wissen , wie man die Ruffini-Regel anwendet . Deshalb hinterlassen wir Ihnen diesen Link für den Fall, dass Sie sich zunächst einmal ansehen möchten, wie das Verfahren aussah.

Um ein Polynom zu faktorisieren, müssen die folgenden Schritte befolgt werden:

1. Die Wurzeln des Polynoms werden nach der Ruffini-Regel berechnet.
2. Jede gefundene Wurzel vom Typ x=a wird in Form eines Faktors (xa) ausgedrückt.
3. Das faktorisierte Polynom ist das Produkt aller gefundenen Faktoren multipliziert mit dem Koeffizienten des Termes höchster Ordnung des ungewichteten Polynoms.

Damit Sie sehen können, wie das geht, und die Vorgehensweise bei der Faktorisierung von Polynomen besser verstehen, finden Sie im Folgenden ein konkretes Beispiel, das Schritt für Schritt erklärt wird:

• Faktorisieren Sie das folgende Polynom:

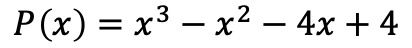
Als Erstes müssen die Nullstellen bzw. Nullstellen des Polynoms berechnet werden. Dazu müssen wir die Teiler des unabhängigen Termes des Polynoms finden, die in diesem Fall ±1, ±2 und ±4 sind.

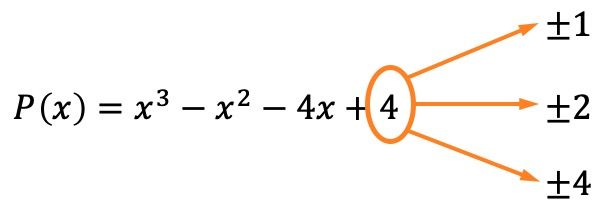
Jetzt wissen wir dank des Rest- und Faktorensatzes, dass, wenn der Rest der Division des Polynoms durch einen dieser Werte gleich 0 ist, dies bedeutet, dass dieser Wert eine Wurzel des Polynoms ist.

Wir müssen daher das Polynom durch jeden Teiler des unabhängigen Termes mit der Ruffini-Regel dividieren und sehen, in welchen Fällen der Rest Null ist.

Zum Beispiel beginnen wir mit der Anwendung der Ruffini-Regel mit

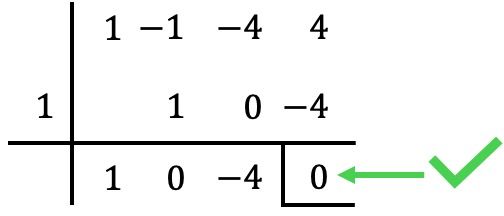
In diesem Fall ist der Rest (oder Rest) der Division Null, also

Es ist eine Wurzel des Polynoms. ✅

Perfekt, wir haben bereits eine Wurzel des Polynoms, es müssen nur noch die anderen verbleibenden Wurzeln bestimmt werden. Dazu verwenden wir beispielsweise die Ruffini-Regel mit einem anderen Teiler des unabhängigen Termes

Außerdem ist es nicht nötig, Ruffinis Methode mit dem ganzzahligen Polynom zu verwenden, sondern wir können dort weitermachen, wo wir im vorherigen Schritt aufgehört haben:

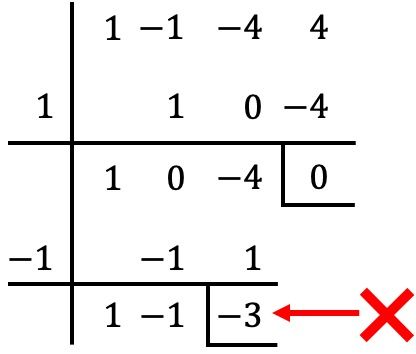
In diesem Fall jedoch beim Teilen durch

Der erhaltene Rest ist also von 0 verschieden

Es ist keine Wurzel des Polynoms. ❌

Wir müssen daher einen anderen Wert ausprobieren, beispielsweise mit der Ruffini-Regel

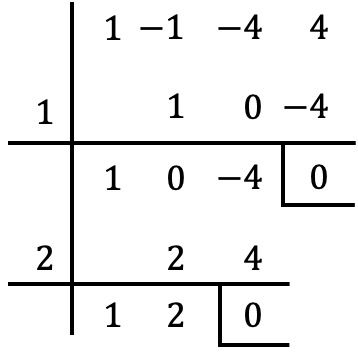
In diesem Fall erhalten wir wieder einen Rest von Null, also

Es ist auch eine Wurzel des Polynoms.

Und wir wenden weiterhin das gleiche Verfahren an. Jetzt prüfen wir, ob

Ist es eine Wurzel des Polynoms oder nicht:

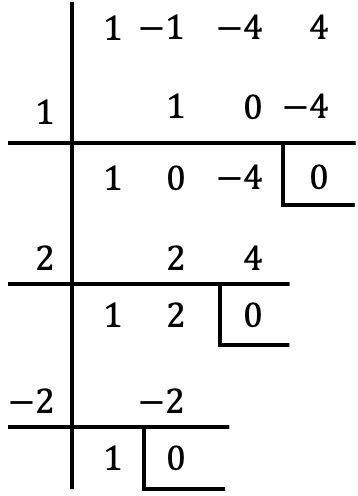
Durch Division durch

Mit der Ruffini-Regel erhalten wir einen Rest von Null, also

ist eine Wurzel oder Nullstelle des Polynoms.

Wir können die Regel von Ruffini daher nicht mehr weiter anwenden, wir haben also bereits alle Wurzeln des Polynoms gefunden, die sind:

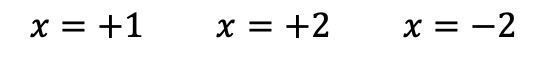
Sobald wir alle Wurzeln des Polynoms bestimmt haben, können wir es faktorisieren. Drücken Sie dazu einfach jede Wurzel aus

in Form eines Faktors vom Typ

, das heißt, dass Sie für jede Wurzel eine Klammer mit a setzen müssen

und die Wurzel hat das Vorzeichen geändert:

Und da wir nun alle Wurzeln als Faktoren ausgedrückt haben, müssen wir alle Klammern mit dem Koeffizienten des Termes höchsten Grades des ursprünglichen Polynoms multiplizieren:

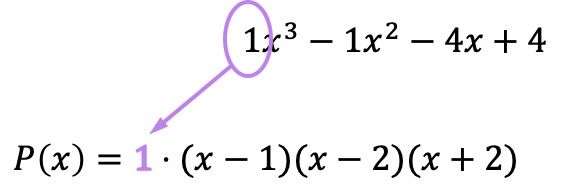
Obwohl in diesem Fall der Koeffizient 1 ist und daher keinen Einfluss auf das Ergebnis hat, ist es wichtig, diese Multiplikation durchzuführen. Denn wenn dieser Koeffizient ungleich 1 wäre, würde sich das faktorisierte Polynom ändern, und wenn wir die Zahl nicht eingeben, würden wir einen Fehler bei der Faktorisierung des Polynoms machen.

Kurz gesagt ist das faktorisierte Polynom:

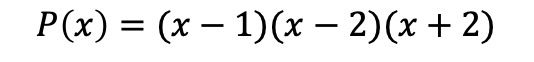
Faktorisierung von Polynomen ohne unabhängigen Term

Wir haben gerade gesehen, dass der unabhängige Term für die Faktorisierung von Polynomen wichtig ist, da er uns ermöglicht, die möglichen Wurzeln des Polynoms zu identifizieren. Wie faktorisiert man jedoch ein Polynom, das keinen unabhängigen Term hat?

Um ein Polynom ohne unabhängigen Term zu faktorisieren , muss man zuerst den gemeinsamen Faktor des Polynoms extrahieren und dann die Wurzeln des Polynoms ohne den gemeinsamen Faktor mithilfe der Ruffini-Regel extrahieren.

So geschrieben klingt es vielleicht etwas kompliziert, also lösen wir ein Beispiel Schritt für Schritt, damit Sie sehen können, wie man ein Polynom mit einem gemeinsamen Faktor faktorisiert:

• Führen Sie die faktorielle Zerlegung des folgenden Polynoms durch:

Wie Sie sehen können, hat das Polynom im Problem keinen unabhängigen Term, daher müssen wir den gemeinsamen Faktor des Polynoms verwenden. Wenn wir genau hinsehen, haben alle Elemente des Polynoms mindestens eines

Der gemeinsame Faktor ist also

Daher erhalten wir beim Extrahieren des gemeinsamen Faktors aus dem Polynom den folgenden Ausdruck:

Und sobald wir den gemeinsamen Faktor des Polynoms extrahiert haben, wenden wir die Regel von Ruffini an, um die Wurzeln des in Klammern gruppierten Polynoms zu berechnen (mit dem Verfahren, das wir im vorherigen Abschnitt gesehen haben):

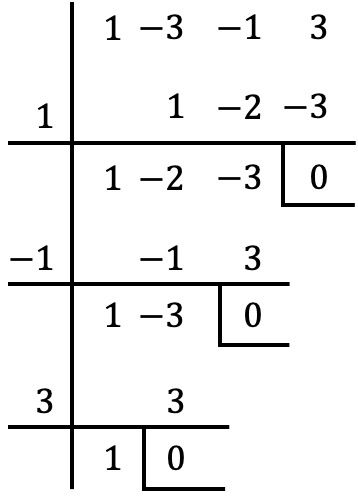
Die Wurzeln oder Nullstellen des Polynoms in Klammern sind also:

Um das Polynom zu faktorisieren, ersetzen Sie einfach das Polynom in Klammern durch seine Wurzeln in Faktorform (wie im Abschnitt oben erklärt):

Und auf diese Weise haben wir bereits das Polynom faktorisiert, das keinen Term vom Grad 0 hatte. Beachten Sie, dass der einzige Unterschied darin besteht, dass wir zuerst einen gemeinsamen Faktor extrahieren müssen, aber alle folgenden Schritte sind genau gleich.

Andererseits sollte man das wissen

Es ist auch eine Wurzel des Polynoms, denn wenn wir den gemeinsamen Faktor extrahieren, bedeutet dies, dass eine der Wurzeln des Polynoms ist

Alle Wurzeln des Polynoms lauten also wie folgt:

Tatsächlich muss das Polynom so viele Wurzeln haben, wie sein Grad angibt. In diesem Fall hat das Polynom den Grad 4 und hat daher 4 Wurzeln.

Faktorisieren von Polynomen mit rationalen Wurzeln

Bisher haben wir Beispiele für die Faktorisierung von Polynomen mit ganzzahligen Wurzeln gesehen, ein Polynom kann jedoch auch rationale Wurzeln haben, also mit Brüchen. Sehen wir uns anhand eines Beispiels an, wie diese Art der Polynomfaktorisierung gelöst wird:

• Faktorisieren Sie das folgende unvollständige Polynom:

Wie immer verwenden wir die Ruffini-Regel mit den Teilern des unabhängigen Termes, um zu versuchen, die Wurzeln des Polynoms zu bestimmen:

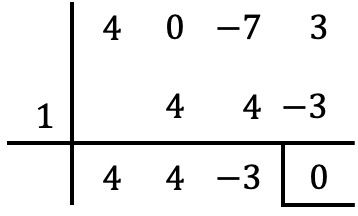
Aber wir können mit Ruffini nicht mehr Wurzeln berechnen, denn wenn wir versuchen, Ruffini mit allen anderen Teilerzahlen des unabhängigen Termes zu berechnen, erhalten wir einen Rest ungleich Null.

Wir befinden uns daher in einer Situation, in der es nur noch darum geht

der Rest der Division ist äquivalent zu 0, das bedeutet, dass das Polynom gebrochene Wurzeln haben kann. Um diese Wurzeln zu bestimmen, könnten wir Ruffini mit Brüchen anwenden. Es ist jedoch sehr leicht, bei den Berechnungen Fehler zu machen, und deshalb gehen wir in diesen Fällen normalerweise wie folgt vor:

Wenn wir die Ruffini-Regel nicht mit ganzzahligen Wurzeln weiter anwenden können, müssen wir das zuletzt erhaltene Polynom gleich 0 setzen und die resultierende Gleichung lösen. Die Wurzeln des Polynoms sind also die aus der Gleichung ermittelten Werte.

Wenn die Gleichung hingegen keine Lösung hat, bedeutet dies, dass das Polynom keine Wurzeln mehr hat und daher nicht vollständig faktorisiert werden kann.

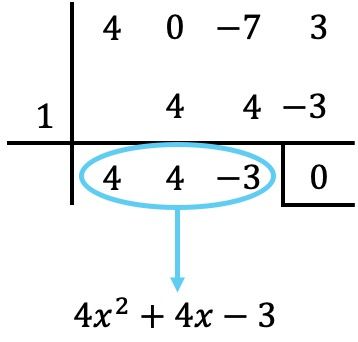
Wir setzen daher das Quotientenpolynom gleich Null:

Und wir verwenden die quadratische Gleichungsformel, um die resultierende Gleichung zu lösen:

Die Wurzeln des Polynoms sind daher:

Das Polynom hat also Wurzeln in Form von Brüchen.

Und sobald wir alle Wurzeln des Polynoms kennen, können wir das faktorisierte Polynom leicht finden, indem wir jede Wurzel ausdrücken

in Form eines Faktors vom Typ

, das heißt, dass Sie für jede Wurzel eine Klammer mit a setzen müssen

und die Wurzel hat das Vorzeichen geändert:

Denken Sie daran, dass Sie zum Faktorisieren eines Polynoms auch seine Faktoren mit dem Koeffizienten des Termes höchster Ordnung des unfaktorisierten Polynoms multiplizieren müssen, der in diesem Fall 4 beträgt.

Sonderfälle der Faktorisierung von Polynomen

Normalerweise wird die Ruffini-Regel (oder synthetische Division) zur Faktorisierung eines Polynoms verwendet, wie oben erläutert. Aber abhängig vom Polynom des Problems können Sie die Polynomfaktorisierung manchmal schneller durchführen. Wir werden jeden dieser besonderen Fälle weiter unten sehen.

Berücksichtigung bemerkenswerter Identitäten

Wenn wir sehen, dass ein Polynom einer bemerkenswerten Identität (oder einem bemerkenswerten Produkt) entspricht, ist es sehr einfach, es zu faktorisieren. Um dies tun zu können, müssen Sie jedoch die Formeln für bemerkenswerte Identitäten beherrschen. Ansonsten empfehle ich Ihnen, einen Blick auf diesen Link zu werfen, wo Sie nicht nur die Formeln finden, sondern auch Beispiele für bemerkenswerte Identitäten sehen können. Identitäten und Sie können sogar Übungen mit ihnen durchführen, die Schritt für Schritt gelöst werden.

Differenz der Quadrate

Wie Sie wissen, lautet die Formel für die bemerkenswerte Identität der Quadratdifferenz wie folgt:

Wenn wir also ein Polynom finden, das den Ausdruck erfüllt

können direkt berücksichtigt werden.

Schauen Sie sich das folgende Beispiel an, in dem eine Quadratdifferenz berücksichtigt wird:

Andererseits sind die Wurzeln des Polynoms:

Weitere Beispiele für die Faktorisierung von Binomialen, die Differenzen von Quadraten sind:

Additions- und Subtraktionsquadrat

Sie sollten bereits die Formeln für die beiden verbleibenden wichtigen Identitäten kennen: das Additionsquadrat und das Subtraktionsquadrat.

Wenn wir also erkennen, dass ein Polynom einer dieser beiden bemerkenswerten Identitäten entspricht, können wir es direkt faktorisieren. Schauen Sie sich die folgenden Beispiele an:

Die Identifizierung dieser bemerkenswerten Produkttypen ist etwas schwieriger. Ein Trick besteht darin, zu überprüfen, ob der unabhängige Term des Polynoms das Quadrat einer Zahl ist und ob der Term höheren Grades das Quadrat eines Monoms ist (normalerweise).

), in diesem Fall reicht es aus, zu überprüfen, ob das wahr ist

entspricht dem Abschluss des Vordiploms.

Wenn wir zum Beispiel das folgende Polynom haben:

In diesem Fall kann es sich nur um das Quadrat einer Summe handeln, da alle Elemente des Polynoms positiv sind. Also die Variable

der Formel muss 5 sein, da es die Wurzel des unabhängigen Termes und der Variablen ist

es muss sein

, da es die Wurzel des Begriffs Mai Grad ist.

Jetzt müssen wir nur noch beweisen, dass die Formel für das Quadrat der Summe mit dem Zwischengradterm erfüllt ist:

✅

Die Formel für das bemerkenswerte Produkt ist erfüllt, daher lautet das faktorisierte Polynom:

Und die Wurzel dieses Polynoms ist

Dies ist eine Doppelwurzel, da ihr Faktor quadriert ist (sie wird zweimal wiederholt).

Nachfolgend finden Sie weitere Beispiele für die Faktorisierung perfekter quadratischer Trinome:

Faktorisierung von Trinomen zweiten Grades

Wie wir gerade gesehen haben, gibt es manchmal Trinome, die perfekte Quadrate sind, und diese können direkt mit den Formeln für bemerkenswerte Identitäten faktorisiert werden. Aber die meisten Trinome sind keine bemerkenswerten Produkte. Wie faktorisieren wir also diese Fälle von Polynomen?

Um ein quadratisches Polynom zu faktorisieren, ist es nicht notwendig, die Ruffini-Methode anzuwenden, sondern einfach das Polynom gleich Null zu setzen und die resultierende quadratische Gleichung zu lösen. Die Lösungen der Gleichung sind daher die Wurzeln des Polynoms.

Wenn wir beispielsweise gebeten werden, das folgende Polynom vom Grad 2 zu faktorisieren:

Anstatt Ruffini zu verwenden, setzen wir das Polynom gleich 0:

Und jetzt verwenden wir die Formel der Gleichung 2. Grades, um die Lösungen der Gleichung zu finden:

Die Wurzeln des Polynoms sind daher:

Und schließlich lautet die Polynomfaktorisierung:

Faktorisieren von Trinomen vierten Grades mit geraden Exponenten

Um ein Polynom vierten Grades mit geraden Exponenten zu faktorisieren, müssen wir wie im vorherigen Fall das Polynom gleich Null setzen und die Biquadratgleichung lösen. Damit die gefundenen Werte den Wurzeln des Polynoms entsprechen.

Als Beispiel faktorisieren wir das folgende Polynom vom Grad 4:

Zuerst setzen wir das Polynom gleich Null:

Jetzt müssen wir die Biquadratgleichung lösen. Dazu nehmen wir eine Variablenänderung vor:

Wir lösen die quadratische Gleichung mit der Formel:

Wir heben die Änderung der Variablen auf, um die Wurzeln zu berechnen:

Die Wurzeln des Polynoms lauten daher:

Und sobald wir die Wurzeln oder Nullstellen des Polynoms kennen, faktorisieren wir es, indem wir seine Wurzeln algebraisch in Form von Faktoren ausdrücken:

Faktorisierung von Polynomen durch Gruppierung

In einigen ganz besonderen Fällen kann eine Formel verwendet werden, um einen ganz bestimmten Polynomtyp zu faktorisieren.

Wenn wir ein Polynom der folgenden Form haben:

Wir können das Polynom vereinfachen, indem wir den gemeinsamen Faktor entfernen:

Und das Polynom kann weiter vereinfacht werden, indem der gemeinsame Faktor ein zweites Mal extrahiert wird:

Auf diese Weise konnten wir das Polynom faktorisieren, ohne Ruffini oder eine andere Methode anzuwenden. Und die Wurzeln dieses Polynoms wären:

Sehen wir uns nun diese Methode anhand eines numerischen Beispiels an:

Zuerst entfernen wir den gemeinsamen Faktor mit

und mit 2:

Und so wie jetzt

ein gemeinsamer Faktor des Polynoms ist, extrahieren wir den gemeinsamen Faktor von

Die Wurzeln des Polynoms lauten daher:

Diese Methode wird auch Faktorisierung von Polynomen durch doppelte gemeinsame Faktorextraktion genannt. Obwohl dies ein sehr schnelles Verfahren ist, empfehlen wir nicht, diese Art der Faktorisierung durchzuführen, da bei der Faktorisierung mit dieser Methode häufig Fehler gemeldet werden. Darüber hinaus kann, wie wir oben gesehen haben, ein Polynom vom Grad 2 auch durch Lösen einer einfachen quadratischen Gleichung faktorisiert werden. Kurz gesagt: Es passiert nichts, wenn Sie diese Methode nicht gut verstehen.

Abschließend sei darauf hingewiesen, dass es noch weitere komplexere Verfahren zur Polynomfaktorisierung gibt, etwa den LLL-Algorithmus, das Kronecker-Verfahren und das Trager-Verfahren, die aufgrund ihrer mathematischen Schwierigkeit hier nicht erläutert werden.

Aufgaben zur Faktorisierung von Polynomen gelöst

Nachdem Sie alle Arten von Faktorisierungspolynomen kennengelernt haben, empfehlen wir Ihnen, die Lösungsübungen zu üben. Aus diesem Grund haben wir im Folgenden mehrere Schritt-für-Schritt-Übungen zur Faktorisierung von Polynomen vorbereitet. Denken Sie daran, wenn Sie Fragen haben, können Sie diese in die Kommentare schreiben und wir werden sie schnell beantworten.

Übung 1

Führen Sie die Faktorisierung des folgenden Polynoms 3. Grades durch:

Es ist ein vollständiges, geordnetes Polynom dritten Grades und letztlich unabhängig. Daher wenden wir Ruffinis Methode an, um die Wurzeln des Polynoms zu bestimmen:

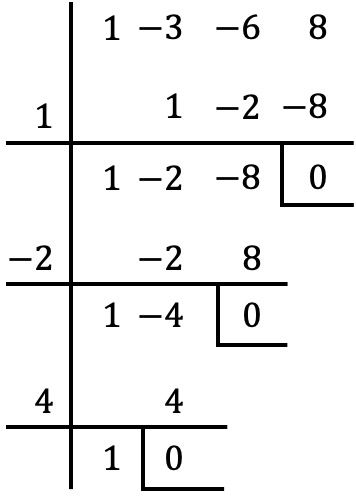
Die Wurzeln des Polynoms lauten daher wie folgt:

Die Polynomfaktorisierung lautet daher:

Übung 2

Berechnen Sie die Faktorisierung des folgenden Polynoms 4. Grades:

Es handelt sich um ein Polynom vierten Grades und mit einem unabhängigen Term. Wir verwenden daher die Ruffini-Methode, um die Wurzeln des Polynoms zu finden:

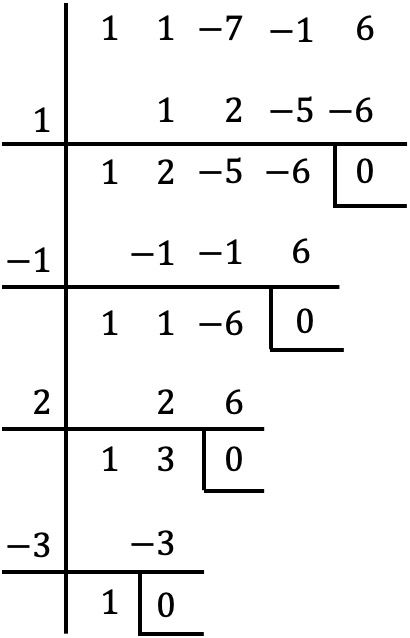
Die Wurzeln des Polynoms lauten daher:

Und wenn wir das Polynom faktorisieren, bleibt Folgendes übrig:

Übung 3

Finden Sie die Faktorisierung des folgenden Polynoms vierten Grades:

In diesem Fall hat das Polynom keinen unabhängigen Term, wir müssen zuerst einen gemeinsamen Faktor extrahieren:

Nachdem wir nun den gemeinsamen Faktor von x genommen haben, berechnen wir die Wurzeln oder Nullstellen des Polynoms in Klammern mit der Methode von Ruffini:

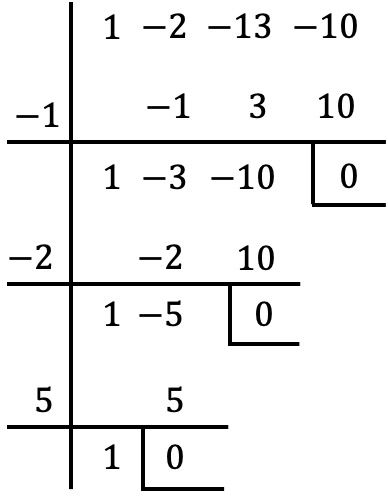
Somit sind die Wurzeln des Polynoms diejenigen, die wir mit der Ruffini-Methode gefunden haben, plus x=0 des gemeinsamen Faktors:

Und schließlich erhalten wir durch die Zerlegung des Polynoms in Faktoren den folgenden Ausdruck:

Übung 4

Wandeln Sie das folgende Polynom dritten Grades in Faktoren um:

Dieses Polynom hat einen unabhängigen Term, daher berechnen wir seine Wurzeln mit dem Ruffini-Algorithmus:

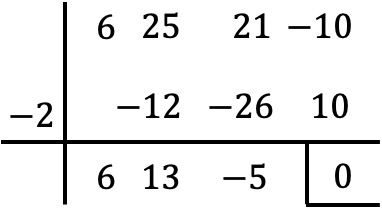
Wenn wir jedoch an diesem Punkt angelangt sind, können wir Ruffinis Regel nicht weiter anwenden, da ohne eine weitere ganze Zahl der Rest der Division Null ist.

Daher setzen wir das resultierende Polynom gleich Null:

Und wir wenden die Formel quadratischer Gleichungen an, um die resultierende Gleichung zu lösen:

Die Wurzeln oder Nullstellen des Polynoms sind daher:

Die Faktorisierung des Polynoms muss also mit Brüchen erfolgen:

Übung 5

Bestimmen Sie die Faktorisierung des folgenden Polynoms 6. Grades:

Das Polynom im Problem hat keinen unabhängigen Term, daher müssen wir zuerst den gemeinsamen Faktor extrahieren, was in diesem Fall der Fall ist

Und sobald wir den gemeinsamen Faktor aus dem Polynom entfernt haben, finden wir die Wurzeln des Polynoms in Klammern unter Verwendung der Ruffini-Regel:

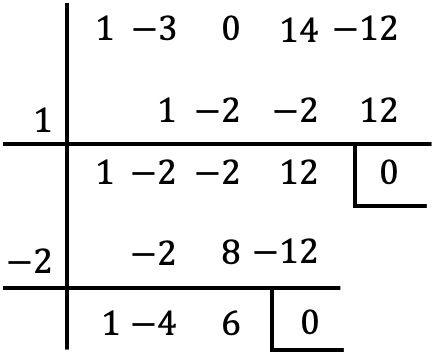
Aber wenn wir dieses Stadium erreicht haben, können wir nicht weitermachen, denn ohne eine weitere ganze Zahl ist der Rest Null.

Wir setzen daher das erhaltene Polynom gleich Null:

Und wir lösen die quadratische Gleichung mit der Formel:

Es gibt keine Wurzeln negativer Zahlen, daher hat die Gleichung keine Lösung, was bedeutet, dass wir keine weiteren Wurzeln des Polynoms finden können. Mit anderen Worten: Das Polynom ist nicht vollständig faktorisierbar.

Die Wurzeln, die wir finden konnten, sind jedoch:

Beachten Sie, dass die Wurzel

wird zweimal wiederholt, weil wir den gemeinsamen Faktor entfernt haben

und da es quadriert ist, bedeutet dies, dass es sich um eine Doppelwurzel handelt.

Zusammenfassend ist das faktorisierte Polynom das Produkt aller gefundenen Wurzeln, ausgedrückt als Faktoren

multipliziert mit dem aus Ruffinis Regel erhaltenen Polynom, das nicht weiter berücksichtigt werden konnte:

Übung 6

Führen Sie die Faktorisierung aller folgenden Polynome durch:

Das Polynom in Abschnitt A) entspricht einer bemerkenswerten Identität, insbesondere dem Quadrat der Summe. Seine Faktorisierung ist daher:

Das Polynom des Abschnitts B) ist ebenfalls ein bemerkenswertes Produkt, insbesondere ist es die Differenz der Quadrate, daher:

Ebenso ist das Polynom in Abschnitt C) eine bemerkenswerte Gleichheit, insbesondere besteht es aus dem Quadrat einer Subtraktion. Seine Faktorisierung ist daher:

Schließlich ist das Polynom in Teil D) keine bemerkenswerte Identität. Wir müssen daher das Polynom gleich 0 setzen und die resultierende Gleichung lösen, um ihre Wurzeln zu finden:

Wir verwenden die quadratische Gleichungsformel:

Die Wurzeln des Polynoms D) sind daher:

Und schließlich ist das Ergebnis der Polynomfaktorisierung: