▷ So entfernen (oder extrahieren) Sie den gemeinsamen Faktor ✅ (gelöste Übungen)

Auf dieser Seite erklären wir, wie man den gemeinsamen Faktor eines Polynoms ermittelt (oder extrahiert). Hier finden Sie die verschiedenen Arten des gemeinsamen Faktors und können einige Beispiele dafür sehen, wie dies erreicht wird. Darüber hinaus können Sie mit Schritt für Schritt gelösten Übungen trainieren.

Was ist der gemeinsame Faktor?

In der Mathematik ist der gemeinsame Faktor ein Faktor, der in allen Termen eines Polynoms vorhanden ist, d. h. der gemeinsame Faktor besteht aus einer Zahl oder einem Buchstaben, der jeden Term eines Polynoms multipliziert.

Als Beispiel ermitteln wir den gemeinsamen Faktor des folgenden Polynoms:

$4x+4y$

Bei Nummer 4 wird es in allen Termen des Polynoms wiederholt:

$\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y$

Der gemeinsame Faktor dieses Polynoms ist daher gleich 4.

$\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}$

So erhalten (oder extrahieren) Sie den gemeinsamen Faktor

Sobald wir die Bedeutung des gemeinsamen Faktors kennen, wollen wir sehen, wie wir den gemeinsamen Faktor aus einem Polynom ermitteln.

Wenn zwei oder mehr Terme eines Polynoms einen gemeinsamen Faktor haben, kann der gemeinsame Faktor verwendet (oder extrahiert) werden, um Additionen oder Subtraktionen des Polynoms in eine Multiplikation umzuwandeln.

Dies mag etwas schwierig zu schreiben erscheinen, also sehen wir uns anhand eines Beispiels an, wie man den gemeinsamen Faktor aus einem Polynom extrahiert:

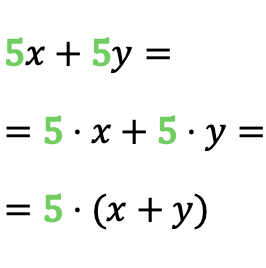
Extrahieren oder entfernen Sie den gemeinsamen Faktor aus einem Polynom

Wie Sie im Beispiel sehen können, wiederholt sich die Zahl 5 im Monom 5x und im Monom 5y, sodass der gemeinsame Faktor des Polynoms 5 ist. Sobald wir also den gemeinsamen Faktor identifiziert haben, können wir die Summe der Monome in a umwandeln Produkt.

Vergessen Sie nicht, beim Extrahieren des gemeinsamen Faktors die Klammern zu setzen, da der gemeinsame Faktor alle Addenden multiplizieren muss.

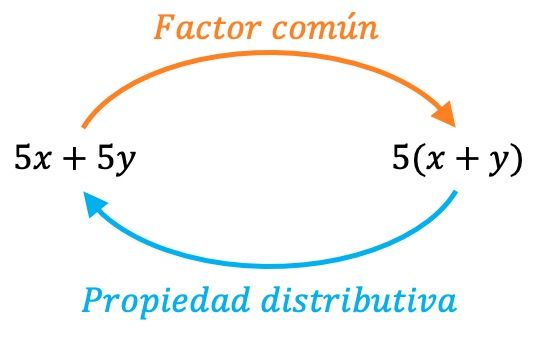
Das Entfernen des gemeinsamen Faktors ist die umgekehrte Operation der Verteilungseigenschaft , das heißt, wir wenden die Verteilungseigenschaft tatsächlich in umgekehrter Reihenfolge an. Daher können wir jederzeit überprüfen, ob wir den gemeinsamen Faktor korrekt extrahiert haben, indem wir den umgekehrten Vorgang ausführen:

Wenn wir durch Anwendung der Verteilungseigenschaft von Anfang an das gleiche Polynom erhalten, bedeutet dies, dass wir den gemeinsamen Faktor korrekt erhalten haben.
Wenn andererseits das Ergebnis der Verwendung der Verteilungseigenschaft ein anderes Polynom ist, das sich vom ursprünglichen Polynom unterscheidet, bedeutet dies, dass wir bei der Extraktion des gemeinsamen Faktors einen Fehler gemacht haben.

gemeinsamer Faktor und Verteilungseigentum

Beispiele für die gemeinsame Faktornahme (oder Extraktion)

Wir überlassen Ihnen weitere Beispiele, um das Konzept des gemeinsamen Faktors zu verstehen:

Beispiel 1

Wie Sie in diesem Beispiel sehen, kann ein gemeinsamer Faktor aus mehr als zwei Termen gleichzeitig extrahiert werden:

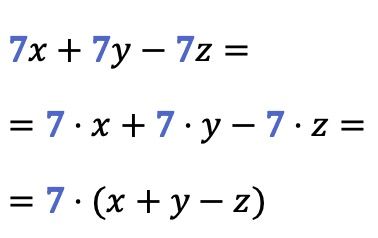
Beispiel 2

Sie können auch einen gemeinsamen Faktor aus den Variablen (oder Buchstaben) extrahieren:

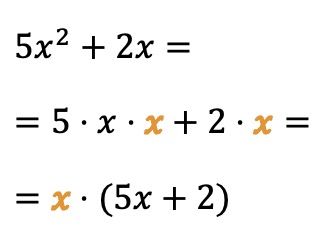
Extrahieren Sie den gemeinsamen Faktor in algebraischen Ausdrücken

In diesem Fall multipliziert der Buchstabe x die beiden Terme des Polynoms, sodass wir den algebraischen Ausdruck vereinfachen können, indem wir die Variable x als gemeinsamen Faktor verwenden.

Beispiel 3

In diesem Beispiel wird im ersten Term die Variable x mit 3 potenziert und im zweiten Term wird x mit 2 potenziert, sodass beide Terme zwei x haben. Der gemeinsame Faktor ist also nicht nur ein x, sondern x ² :

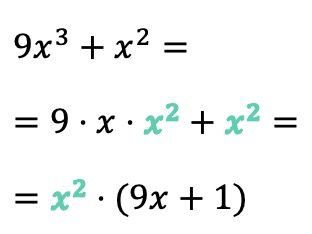
Algebra gemeinsamer Faktor von x im Quadrat

Beachten Sie andererseits, dass wir beim Extrahieren des gemeinsamen Faktors eine 1 an seine Stelle setzen müssen, wenn der gemeinsame Faktor des Polynoms genau mit einem Term übereinstimmt . Andernfalls würden wir keinen äquivalenten Ausdruck erhalten, wenn wir nichts an seine Stelle setzen würden.

wie man einen gemeinsamen Faktor extrahiert oder findet

Beispiel 4

Manchmal ist der gemeinsame Faktor nicht so offensichtlich und nicht direkt sichtbar, sondern er ist ein Teiler der Koeffizienten von Monomen. Der gemeinsame Faktor im folgenden Beispiel ist beispielsweise 3, da die faktorielle Zerlegung von 6 und 9 3 enthält:

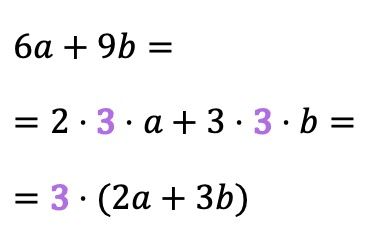
Diese Art von gemeinsamem Faktor wird in einigen Algebrabüchern als maximaler gemeinsamer Faktor bezeichnet, da der gemeinsame Faktor gleichzeitig der größte gemeinsame Faktor (GCD) der Koeffizienten der Polynomterme ist.

Wenn Sie es bis hierher geschafft haben, wissen Sie wahrscheinlich bereits, wie man den gemeinsamen Faktor eines perfekten Polynoms ermittelt. Haben Sie sich jedoch nicht gefragt, wozu der gemeinsame Faktor dient? Nun, eine Anwendung des gemeinsamen Faktors besteht darin, dass er zur Faktorisierung von Polynomen verwendet wird. Wenn Sie immer noch nicht wissen, was es ist, können Sie in diesem Link sehen, was Polynomfaktorisierung ist und warum der gemeinsame Faktor für die Durchführung dieser Polynomoperation so wichtig ist.

Gemeinsamer Faktor für Brüche

Der gemeinsame Faktor ist auch sehr nützlich, um Terme in Brüche mit Polynomen im Zähler und Nenner zu vereinfachen.

Um zu sehen, wie das geht, vereinfachen wir als Beispiel den folgenden Bruch:

$\cfrac{2x^2+4}{14x+8y}$

Als erstes müssen wir den gemeinsamen Faktor des Zählerpolynoms und des Nennerpolynoms ermitteln. In diesem Fall ist der gemeinsame Faktor der beiden Polynome 2:

$\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}$

Jetzt extrahieren wir den gemeinsamen Faktor der beiden Polynome:

$\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}$

Und sobald wir einen gemeinsamen Faktor für beide Polynome erhalten haben, müssen wir die Faktoren entfernen, die sich im Zähler und Nenner wiederholen :

$\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}$

Zusammenfassend ist der vereinfachte Bruch:

$\cfrac{x^2+2}{7x+4y}$

Gemeinsamer Faktor durch Gruppierung

Eine Möglichkeit, die Terme eines Polynoms zu reduzieren, besteht darin, die Methode des gemeinsamen Faktors durch Gruppierung der Terme zu verwenden, die auch als doppelte Extraktion gemeinsamer Faktoren bezeichnet wird. Wie der Name schon sagt, besteht dieses Verfahren darin, den Ausdruck eines Polynoms zu vereinfachen, indem seine Terme zweimal gruppiert werden.

Diese Methode ist etwas komplex, also schauen wir uns an, wie sie Schritt für Schritt mit dem folgenden Polynom angewendet wird:

$x^2+2x+5x+10$

Wir müssen zunächst zwei verschiedene mögliche gemeinsame Faktoren bestimmen, also teilen wir das Polynom in zwei Teile auf:

$(x^2+2x)+(5x+10)$

In diesem Fall haben die Elemente x ² und 2x den Buchstaben x als gemeinsamen Faktor und die Terme 5x und 10 haben 5 als gemeinsamen Faktor (da 10 ein Vielfaches von 5 ist). Diese beiden Faktoren haben wir also gemeinsam:

$(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)$

$x(x+2)+5(x+2)$

Und schließlich können wir das Polynom wie folgt vereinfachen, da die verbleibenden beiden Polynomprodukte den Faktor (x+2) haben:

$(x+2)\cdot (x+5)$

Wie Sie sehen, ist diese Methode überhaupt nicht einfach. Zögern Sie also nicht, uns Ihre Fragen in den Kommentaren zu stellen. Wir werden sie so schnell wie möglich beantworten.

Übungen zu häufigen Faktoren werden Schritt für Schritt gelöst

Wir hinterlassen Ihnen einige Übungen, die Schritt für Schritt gelöst werden, damit Sie üben können, den gemeinsamen Faktor aus einem Polynom zu extrahieren.

Übung 1

Extrahieren Sie den gemeinsamen Faktor aus den folgenden Polynomen:

$\text{A)} \ 6a+6b$

$\text{B)} \ 3x^2+8x$

$\text{C)} \ 2x-4$

$\text{D)} \ -5x^4+x^2$

Sehen Sie sich die Lösung an

A) Alle Terme, aus denen das erste Polynom besteht, haben eine 6, daher ist der gemeinsame Faktor des Polynoms 6:

$6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}$

B) Im zweiten Polynom haben alle seine Elemente mindestens einen Buchstaben x. Hier ist der gemeinsame Faktor des Polynoms:

$3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}$

C) Das erste Monom des Polynoms hat offensichtlich eine 2, und das zweite Monom ist ein Vielfaches von 2. Der gemeinsame Faktor des Polynoms ist also 2:

$2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}$

D) Im letzten Polynom sind alle Variablen mindestens quadriert. Der gemeinsame Faktor ist also x ² :

$-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}$

Denken Sie daran, dass, wenn der gemeinsame Faktor mit einem Term identisch ist, an seiner Stelle eine 1 eingesetzt werden muss.

Übung 2

Betrachten Sie den gemeinsamen Faktor der folgenden Polynome:

$\text{A)} \ 8x^2 + 10y^3$

$\text{B)} \ 5x^3-2x^2+4x$

$\text{C)} \ 25x^5+15x^3-20$

$\text{D)} \ 9x^4-3x^3-21x^2-6x$

Sehen Sie sich die Lösung an

A) Alle Koeffizienten der Elemente, aus denen das erste Polynom besteht, sind Vielfache von 2, daher wird das Polynom durch Extrahieren des gemeinsamen Faktors zu:

$\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}$

B) In allen Termen des Polynoms gibt es mindestens ein x, also:

$\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}$

C) Der größte gemeinsame Teiler der Koeffizienten aller Terme des Polynoms ist 5, sodass der gemeinsame Teiler des Polynoms 5 ist:

$\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}$

D) Alle Terme im Polynom haben mindestens ein x und außerdem sind alle Koeffizienten Vielfache von 3. Daher ist der gemeinsame Faktor des Polynoms 3x:

$\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}$

Übung 3

Finden Sie den gemeinsamen Faktor jedes der folgenden Polynome und subtrahieren Sie ihn:

$\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4$

$\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5$

$\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c$

$\text{D)} \ 18x^2y+10xy-5xy^3+4z$

Sehen Sie sich die Lösung an

A) Alle Monome haben mindestens den Buchstaben

$a$

im Quadrat und der Buchstabe

$b$

gewürfelt, also ist der gemeinsame Faktor

$a^2b^3:$

$\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}$

B) Alle Koeffizienten des Polynoms sind Vielfache von 8 und haben außerdem mindestens x ² und y ² als Literalteile. Der gemeinsame Faktor des Polynoms ist daher 8x ² y ² .

$\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}$

C) In diesem Fall stimmt der gemeinsame Faktor mit dem Wert des Zwischenmonomins überein

$\left(6ab^2c\right)$

, da die Koeffizienten der anderen Monome Vielfache von sind

$6$

und das hat absolut jeder

$ab^2c:$

$\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}$

D) In diesem speziellen Fall hat das Polynom keinen gemeinsamen Faktor, da kein Faktor in allen Gliedern des Polynoms wiederholt wird. Daher kann der Polynomausdruck nicht algebraisch vereinfacht werden.

$18x^2y+10xy-5xy^3+4z$

Übung 4

Vereinfachen Sie die folgenden algebraischen Brüche, indem Sie den gemeinsamen Faktor verwenden:

$\text{A)} \ \cfrac{10x^2+30}{5x-20}$

$\text{B)} \ \cfrac{16x^2-8}{24x-32}$

$\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}$

$\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}$

Sehen Sie sich die Lösung an

Das Verfahren zur Vereinfachung eines algebraischen Bruchs, also eines Bruchs mit Polynomen, besteht darin, den gemeinsamen Faktor aus Zähler und Nenner des Bruchs zu extrahieren und dann die Faktoren zu eliminieren, die sich oben und unten wiederholen. unterhalb des Bruchs. ALSO:

$\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}$

$\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}$

$\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}$

$\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}$

Übung 5

Nehmen Sie den gemeinsamen Faktor der folgenden Polynomausdrücke:

$\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}$

$\text{B)} \ \sqrt{12x^3+16}$

$\text{C)} \ x^2+4x-3x-12$

$\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}$

Sehen Sie sich die Lösung an

A) Alle Terme des Polynoms können faktoriell in die dritte zerlegt werden, daher:

$\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}$

B) Der gemeinsame Faktor des Polynoms innerhalb der Wurzel ist 4, aber dann können wir den gemeinsamen Faktor durch Berechnen seiner Quadratwurzel ausgeben:

$\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}$

C) In diesem Polynom können wir den Prozess des Extrahierens des gemeinsamen Faktors durch Gruppieren anwenden:

$\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}$

D) Alle Bruchkoeffizienten des Polynoms sind Vielfache der Hälfte, daher beträgt der gemeinsame Faktor des Polynoms ½.

$\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}$

👇👇👇 Wie fandest du die Erklärung? Hat es Ihnen gefallen? Denken Sie auch daran: Wenn Sie Fragen zur Bestimmung des gemeinsamen Teilers eines Polynoms haben oder eine Übung nicht verstehen, können Sie uns diese jederzeit in den Kommentaren stellen und wir werden Ihnen antworten. 👇👇👇

Extrahieren oder entfernen sie den gemeinsamen faktor

Was ist der gemeinsame Faktor?

So erhalten (oder extrahieren) Sie den gemeinsamen Faktor

Beispiele für die gemeinsame Faktornahme (oder Extraktion)

Beispiel 1

Beispiel 2

Beispiel 3

Beispiel 4

Gemeinsamer Faktor für Brüche

Gemeinsamer Faktor durch Gruppierung

Übungen zu häufigen Faktoren werden Schritt für Schritt gelöst

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Kommentar verfassen Kommentieren abbrechen