Exponentialfunktion

Auf dieser Seite erfahren Sie, was Exponentialfunktionen sind und wie Sie eine Exponentialfunktion in einem Diagramm darstellen. Darüber hinaus sehen Sie alle seine Eigenschaften und mehrere Beispiele, um es vollständig zu verstehen. Abschließend können Sie mit Schritt für Schritt gelösten Übungen und Problemen zu Exponentialfunktionen üben.

Was ist eine Exponentialfunktion?

Die Definition einer Exponentialfunktion lautet wie folgt:

Beispiele für Exponentialfunktionen

Die folgenden Funktionen sind Beispiele für Exponentialfunktionen:

Eigenschaften von Exponentialfunktionen

Exponentialfunktionen haben folgende Eigenschaften:

• Der Definitionsbereich einer Exponentialfunktion besteht aus reellen Zahlen, oder anders ausgedrückt: Für jeden Wert von x existiert eine Exponentialfunktion.

• Da die Funktion jedoch nur positive Werte annimmt, besteht der Bereich einer Exponentialfunktion aus positiven reellen Zahlen.

• Jede Exponentialfunktion ist sowohl eine stetige als auch eine injektive Funktion.

• Wenn die Funktion nicht übersetzt wird, verläuft jede Exponentialfunktion durch den Punkt (0,1). Weil die als Null ausgewertete Funktion immer Eins ergibt.

• Ebenso ist der Wert einer Exponentialfunktion bei x=1 gleich der Basis.

• Wenn die Machtbasis

  

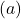
  größer als 1 ist, nimmt die Exponentialfunktion zu. Andererseits, wenn der Koeffizient

  

  liegt im Intervall zwischen 0 und 1, die Exponentialfunktion nimmt ab.

• Im Allgemeinen ist die x-Achse eine horizontale Asymptote einer Exponentialfunktion.

• Die Umkehrung der Exponentialfunktion ist die Logarithmusfunktion. Daher sind die Graphen einer Exponentialfunktion und einer logarithmischen Funktion symmetrisch zur Geraden y=x, wenn beide die gleiche Basis haben.

Wie man eine Exponentialfunktion grafisch darstellt

Exponentialfunktionen sind sehr einfach darzustellen. Sehen wir uns also anhand eines Beispiels an, wie man eine Exponentialfunktion in einem Diagramm grafisch darstellt.

• Zeichnen Sie die folgende Exponentialfunktion in ein Diagramm:

Bei Exponentialfunktionen muss der Definitionsbereich nicht berechnet werden, da es sich immer um reelle Zahlen handelt:

Es reicht daher aus, die Wertetabelle zu erstellen. Da sich diese Art von Funktionen von einem Punkt zum anderen stark ändern, berechnen wir 5 Punkte. Aber je mehr Punkte wir berechnen, desto genauer wird die Darstellung der Funktion.

Um die Punkte in der Wertetabelle zu ermitteln, empfehlen wir die Verwendung eines Taschenrechners, da die manuelle Berechnung schwierig ist.

Jetzt stellen wir die Punkte in einem Diagramm dar :

Und schließlich fügen wir die Punkte zusammen und erweitern die Funktion:

Beachten Sie, dass die Funktion auf der rechten Seite bis ins Unendliche wächst.

Im Gegensatz dazu nimmt die Funktion auf der linken Seite ab, erreicht jedoch nie 0. Auch wenn sie ihr sehr nahe kommt, berührt sie sie nie. Das bedeutet, dass die Linie y=0 (die x-Achse) eine horizontale Asymptote ist.

Aufgaben zu Exponentialfunktionen gelöst

Übung 1

Stellen Sie die folgende Exponentialfunktion grafisch dar:

Da es sich um eine Exponentialfunktion handelt, müssen Sie zu ihrer Darstellung eine Wertetabelle erstellen, die der Variablen x Werte zuordnet:

Sobald wir die Wertetabelle haben, tragen wir die erhaltenen Punkte in das Diagramm ein und zeichnen die Funktion auf:

Beachten Sie, dass die Funktion auf der rechten Seite bis ins Unendliche wächst. Auf der linken Seite hingegen nimmt die Funktion ab, überschreitet jedoch nie 1. Tatsächlich hat die Funktion auf der rechten Seite eine horizontale Asymptote y=1.

In diesem Fall liegt die horizontale Asymptote bei y=1 statt auf der OX-Achse, da eine vertikale Verschiebung um eine Einheit nach oben in Richtung der Funktion vorgenommen wurde.

Übung 2

Zeichnen Sie die folgende Exponentialfunktion in ein Diagramm:

Da es sich um eine Exponentialfunktion handelt, müssen Sie zur grafischen Darstellung eine Wertetabelle erstellen, die der Variablen x Werte angibt:

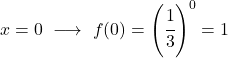
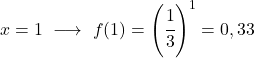
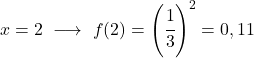
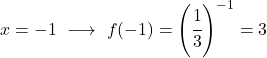
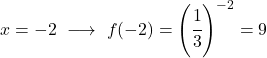
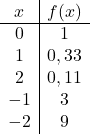
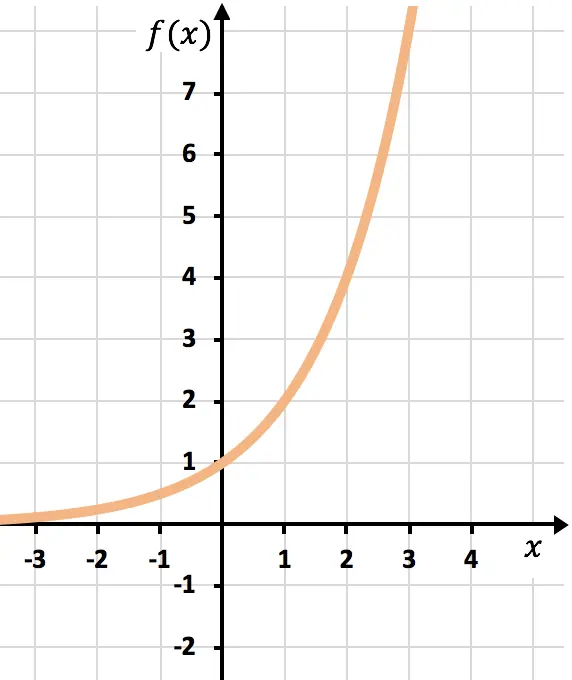
Sobald wir die Wertetabelle haben, tragen wir die berechneten Punkte in das Diagramm ein und zeichnen die Funktion:

Beachten Sie, dass die Funktion auf der linken Seite bis ins Unendliche wächst. Auf der rechten Seite hingegen nimmt die Funktion ab, überschreitet jedoch nie 0. Tatsächlich hat die Funktion eine horizontale Asymptote bei y=0 (der X-Achse).

Übung 3

Zeichnen Sie die folgende Exponentialfunktion in ein Diagramm:

Da es sich um eine Exponentialfunktion handelt, müssen Sie zum Zeichnen eine Wertetabelle erstellen, in der die Funktion an mehreren Punkten bewertet wird:

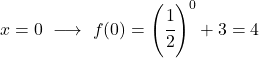
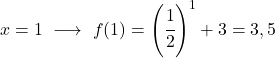
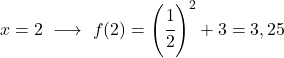
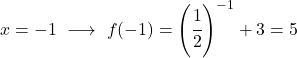
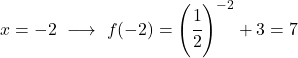
Abschließend stellen wir die erhaltenen Punkte im Diagramm dar und zeichnen die Funktion auf:

Beachten Sie, dass die Funktion auf der linken Seite unbegrenzt bis ins Unendliche wächst. Auf der rechten Seite hingegen nimmt die Funktion ab, überschreitet jedoch nie 3. Tatsächlich hat die Funktion eine horizontale Asymptote bei y=3.

In diesem Fall liegt die horizontale Asymptote bei y=3 statt auf der X-Achse, da die Funktion vertikal um drei Einheiten nach oben verschoben wurde.

Übung 4

Lösen Sie das folgende Problem bezüglich Exponentialfunktionen.

• Bestimmen Sie den Wert von

  

  so dass die nächste Exponentialfunktion durch den Punkt (2.8) verläuft.

Die Funktion muss den Punkt (2,8) durchlaufen, sodass wir die Werte von x und f(x) des Punktes in die Funktion einsetzen können, um den Wert der Konstante k zu ermitteln:

Und nun lösen wir die resultierende Gleichung:

Übung 5

Lösen Sie das folgende Problem bezüglich Exponentialfunktionen.

Eine Termitenpopulation vermehrt sich nach folgender Funktion:

Gold

ist die Anzahl der Termiten und

Die Zeit ist in Monaten vergangen.

Wie viele Termiten wird es nach einem Jahr geben?

Um die Anzahl der Termiten in einem Jahr zu berechnen, setzen Sie einfach die verstrichene Zeit (1 Jahr) in die Funktion ein. Da es sich bei der Funktion t jedoch um die verstrichenen Monate und nicht um die Jahre handelt, müssen wir t = 12 setzen, da ein Jahr 12 Monate hat:

Wir lösen mit dem Taschenrechner:

Nach einem Jahr wird es also 1.594.323 Termiten geben.