Abstand von einem Punkt zu einer Ebene im Raum (Formel)

Auf dieser Seite erfahren Sie, wie der Abstand zwischen einem Punkt und einer Ebene im Raum berechnet wird (Formel). Darüber hinaus können Sie Beispiele sehen und mit Schritt für Schritt gelösten Übungen üben.

Wie groß ist der Abstand von einem Punkt zu einer Ebene?

In der analytischen Geometrie ist der Abstand von einem Punkt zu einer Ebene der kürzeste Abstand zwischen dem Punkt und jedem anderen Punkt auf der Ebene. Dieser Abstand entspricht der Länge des Segments senkrecht zur Ebene, das vom Punkt zur Ebene verläuft.

Formel für den Abstand von einem Punkt zu einer Ebene

Nachdem wir den Begriff des Abstands zwischen einem Punkt und einer Ebene genau kennengelernt haben, sehen wir uns nun die Formel zur Berechnung dieses Abstands an:

Gegeben sei ein Punkt und die allgemeine (oder implizite) Gleichung einer Ebene:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

Die Formel für den Abstand von einem Punkt zu einer Ebene lautet:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Der Beweis der Formel für den Abstand von einem Punkt zu einer Ebene ist ziemlich mühsam und langwierig, deshalb werden wir ihn auf dieser Seite nicht ausführen.

Wenn wir andererseits bei der Anwendung der Formel ein Ergebnis gleich Null erhalten, bedeutet dies offensichtlich, dass der Abstand zwischen dem Punkt und der Ebene Null ist und der Punkt daher Teil dieser Ebene ist.

Beachten Sie abschließend, dass zur Anwendung der Formel der Plan als allgemeine (oder implizite) Gleichung definiert werden muss. Wenn es also durch eine andere Art von Ebenengleichung ausgedrückt würde, müssten wir es zunächst in eine allgemeine Gleichung umwandeln und dann die Formel verwenden.

Beispiel für die Berechnung der Entfernung von einem Punkt zu einer Ebene

Damit Sie sehen können, wie der Abstand zwischen einem Punkt und einer Ebene numerisch ermittelt wird, lösen wir im Folgenden ein Beispiel:

Berechnen Sie den Abstand zwischen Punkt P und Ebene π. Nachdem ich Punkt und Plan gesagt habe:

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

Um den Abstand vom Punkt zur Ebene zu ermitteln, wenden Sie einfach die Formel aus dem obigen Abschnitt an:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Jetzt setzen wir den Wert jeder Unbekannten in die Formel ein:

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

Und schließlich führen wir die Operationen durch:

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

Beachten Sie, dass im Zähler des Bruchs ein absoluter Wert und im Nenner eine Quadratwurzel steht, das Ergebnis also immer positiv sein muss. Dies ist sinnvoll, da Abstände nicht negativ sein können, sondern immer positiv sind.

Berechnen Sie den Abstand zwischen zwei parallelen Ebenen

Zwei parallele Ebenen sind immer gleich weit voneinander entfernt. Um den Abstand zwischen zwei parallelen Ebenen zu ermitteln, können wir daher einen Punkt auf einer der beiden Ebenen nehmen und den Abstand von diesem Punkt zur anderen Ebene berechnen.

Es ist eine Methode zum Ermitteln des Abstands zwischen zwei parallelen Ebenen. Es geht jedoch noch einfacher, wenn die Koeffizienten A, B und C der Gleichungen der beiden Ebenen übereinstimmen:

Betrachten Sie die allgemeinen (oder impliziten) Gleichungen zweier paralleler Ebenen:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

Die Formel zur Berechnung des Abstands zwischen zwei parallelen Ebenen lautet:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

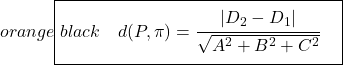
Daher ist es sicherlich einfacher, den Abstand zwischen zwei parallelen Ebenen mithilfe der Formel zu ermitteln, da es nur darum geht, die Formel anzuwenden und das war’s, aber es kommt auf das Problem an. Darüber hinaus halten wir es für am besten, beide Methoden zur Entfernungsberechnung zu erklären, damit Sie die Methode auswählen können, die Ihnen am besten gefällt.

Beispiel für die Berechnung des Abstands zwischen zwei parallelen Ebenen

Als Beispiel berechnen wir den Abstand zwischen den folgenden zwei Ebenen:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Wir müssen zunächst überprüfen, ob es sich um zwei parallele Ebenen handelt. Somit sind alle Koeffizienten der Ebenengleichungen mit Ausnahme der unabhängigen Terme proportional, sodass es sich effektiv um zwei parallele Ebenen handelt.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In diesem Fall stimmen die Terme A, B und C der Gleichungen der beiden Ebenen nicht überein, aber wir können dies erreichen, indem wir die gesamte Gleichung der zweiten Ebene durch zwei teilen:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Die Gleichungen der beiden Ebenen haben also bereits die gleichen Koeffizienten A, B und C. Daher können wir den Abstand zwischen den beiden Ebenen leicht mit der Formel für den Abstand zwischen zwei parallelen Ebenen berechnen:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Wir ersetzen die Werte und lösen die Operationen:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Damit ist der Abstand zwischen einer Ebene und der anderen Ebene gleich Eins.

Entfernungsprobleme von einem Punkt zu einer Ebene lösen

Übung 1

Berechnen Sie den Abstand zwischen dem Punkt P und der Ebene, deren kartesische (oder allgemeine) Gleichung lautet:

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

siehe Lösung

Um den Abstand vom Punkt zur Ebene zu berechnen, müssen Sie die entsprechende Formel verwenden:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Wir setzen den Wert jedes Parameters in die Formel ein:

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

Und schließlich führen wir die Operationen durch:

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

Übung 2

Finden Sie den Abstand zwischen Punkt P und Ebene π:

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

siehe Lösung

Bevor wir die Formel für den Abstand von einem Punkt zu einer Ebene verwenden, müssen wir die Ebene zunächst in Form einer impliziten (oder allgemeinen) Gleichung ausdrücken:

$\pi: \ -5x+y+2z=0$

Und jetzt können wir mit der Formel den Abstand vom Punkt zur Ebene bestimmen:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Wir setzen den Wert jedes Termes in die Formel ein:

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

Und schließlich führen wir die Operationen durch:

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

Übung 3

Verwenden Sie die Formel für den Abstand zwischen einem Punkt und einer Ebene, um zu bestimmen, ob Punkt P in der Ebene π liegt.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

siehe Lösung

Um zu überprüfen, ob der Punkt zur Ebene gehört, können wir den Abstand zwischen den beiden berechnen: Wenn der Abstand Null ist, bedeutet dies, dass der Punkt zur Ebene gehört, wenn der Abstand andererseits von 0 verschieden ist, bedeutet dies, dass der Punkt zur Ebene gehört Der Punkt liegt außerhalb der Ebene. planen.

Daher ermitteln wir den Abstand zwischen Punkt und Ebene anhand der Formel:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

Der Abstand zwischen dem Punkt und der Ebene ist äquivalent zu Null, sodass der Punkt effektiv zur Ebene gehört.

Übung 4

Finden Sie den Abstand zwischen den folgenden zwei Ebenen:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

siehe Lösung

Wir müssen zunächst überprüfen, ob es sich um zwei parallele Ebenen handelt. Mit Ausnahme der unabhängigen Terme sind alle Koeffizienten der Gleichungen der beiden Ebenen proportional, es handelt sich also tatsächlich um zwei parallele Ebenen.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In diesem Fall berechnen wir den Abstand zwischen den beiden Ebenen mit der Formel, da ihre Koeffizienten A, B und C gleich sind:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Also setzen wir die Werte in die Formel ein und führen die Operationen aus:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Übung 5

Ermitteln Sie den Abstand zwischen den folgenden zwei parallelen Ebenen:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

siehe Lösung

Die Vordergrundebene wird in Form parametrischer Gleichungen definiert. Um die Formel für den Abstand zwischen zwei parallelen Ebenen anzuwenden, müssen wir sie zunächst in die Form einer allgemeinen Gleichung umwandeln, was viele Berechnungen und Zeit erfordert. Deshalb geht es schneller, wenn wir einen Punkt auf dieser Ebene nehmen und den Abstand von diesem Punkt zur anderen Ebene berechnen.

Somit entsprechen die Koordinaten eines Punktes, durch den die Ebene π ₁ verläuft, den unabhängigen Termen jeder parametrischen Gleichung:

$P(3,-2,5)$