Auf dieser Seite erklären wir, was die Einheitsmatrix ist und veranschaulichen sie zusätzlich mit mehreren Übungen, damit sie gut verstanden wird. Außerdem erfahren Sie, welche Eigenschaften dieser Matrixtyp für die lineare Algebra so wichtig sind.
Was ist eine einheitliche Matrix?
Die Definition einer Einheitsmatrix lautet wie folgt:
Eine einheitliche Matrix ist eine komplexe Matrix, die multipliziert mit ihrer konjugierten Transponierungsmatrix der Identitätsmatrix entspricht. Das heißt, die folgende Bedingung ist erfüllt:
Gold
ist eine einheitliche Matrix und
seine konjugierte Transponierte.
Daher impliziert diese Bedingung, dass die Umkehrung einer Einheitsmatrix ihre konjugierte Transponierte ist , denn gemäß der Definition einer inversen Matrix ist eine Matrix die Umkehrung einer anderen, wenn ihr Produkt der Matrix d’identify entspricht .
![\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8f035ef94e00b67acffd2881944642f_l3.png "Rendered by QuickLaTeX.com")
Daher ist eine Einheitsmatrix immer eine reguläre oder nicht entartete Matrix , da sie immer eine Umkehrung hat.
Andererseits ist das Analogon einer Einheitsmatrix in einer reellen Zahlenumgebung die orthogonale Matrix , und in diesem Fall ist es wahr, dass die Einheitsmatrix multipliziert mit ihrer Transponierten gleich der Identitätsmatrix ist.
In diesem Fall wäre die inverse Matrix von U also direkt ihre transponierte (oder transponierte) Matrix.
Beispiele für Einheitsmatrizen
Beispiel einer Einheitsmatrix der Dimension 2×2
Sobald wir das Konzept der Einheitsmatrix kennengelernt haben, sehen wir uns zum besseren Verständnis ein Beispiel einer 2×2-Einheitsmatrix an:
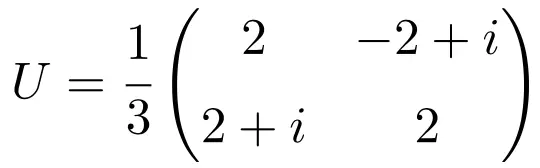
Diese Matrix ist einheitlich, da die Multiplikation ihrer selbst mit ihrer konjugierten Matrix die Identitätsmatrix (oder Einheitsmatrix) ergibt:
![\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-11df575022f8a50881fedc994f4f12af_l3.png "Rendered by QuickLaTeX.com")
Und wie wir zuvor gesehen haben, ist jede einheitliche Matrix mit ihrer konjugierten Transponierten vertauschbar:
![\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4848f3eab836be0996049e221bb8a8c3_l3.png "Rendered by QuickLaTeX.com")
Beispiel für eine Einheitsdiagonalmatrix
Die Diagonalmatrix , die nur aus der komplexen Zahl i besteht, ist ebenfalls ein Beispiel für eine einheitliche Matrix, unabhängig von der Dimension der Matrix. Unten finden Sie eine gelöste Übung, die dies anhand einer Einheitsmatrix der Dimension 3 × 3 veranschaulicht:
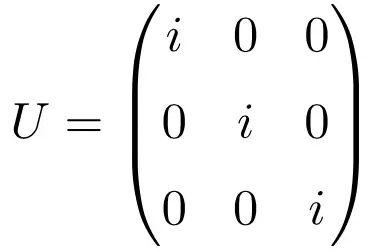
Beachten Sie, dass, wenn wir das Produkt der Matrix durch ihre konjugierte Transponierte lösen, dies die Identitätsmatrix als Lösung ergibt:
![\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61bc73f95b9c2515595fe3ed2e18df3f_l3.png "Rendered by QuickLaTeX.com")
Und das Gleiche passiert, wenn wir die Matrizen umgekehrt multiplizieren:
![\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5cdf7b15d442ec89fde613ba2fd3fe45_l3.png "Rendered by QuickLaTeX.com")
Das Merkmal dieser Matrix besteht darin, dass sie als Beispiel für eine Einheitsmatrix beliebiger Dimension dient, da die Matrix jedes Mal durch die imaginäre Zahl i auf der Hauptdiagonale gebildet wird und die restlichen Elemente Null (0) sind ) wird es eine einheitliche Matrix sein.
Eigenschaften einer einheitlichen Matrix
Die Eigenschaften von Einheitsmatrizen sind wie folgt:
- Offensichtlich ist jede Einheitsmatrix eine Normalmatrix . Obwohl nicht alle normalen Matrizen einheitliche Matrizen sind.
- Unitäre Matrizen sind immer quadratische Matrizen .
- Alle Einheitsmatrizen sind diagonalisierbar, das heißt, sie können in Diagonalmatrizen umgewandelt werden.
- Der Absolutwert der Determinante einer Einheitsmatrix ist immer gleich 1.
- Die identische Matrix ist eine Einheitsmatrix.
- für alle
, die Menge aller Einheitsmatrizen
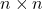
Mit der Matrixproduktoperation bilden sie eine Gruppe, die als Einheitsgruppe bezeichnet wird.
- Die Multiplikation zweier Einheitsmatrizen gleicher Ordnung ergibt also eine weitere Einheitsmatrix.
- Der Modul aller Eigenwerte (oder Eigenwerte) einer Einheitsmatrix ist immer gleich 1.
- Die Eigenräume dieses Matrixtyps sind orthogonal.