Idempotente Matrix

Auf dieser Seite erklären wir, was idempotente Matrizen sind. Wir zeigen Ihnen auch einige Beispiele dieser Art von Matrizen, damit Sie sie vollständig verstehen. Außerdem finden Sie die Formel zum Finden einer idempotenten Matrix und schließlich alle Eigenschaften idempotenter Matrizen.

Was ist eine idempotente Matrix?

Die Definition einer idempotenten Matrix lautet wie folgt:

Eine idempotente Matrix ist diejenige Matrix, die bei Multiplikation mit sich selbst als Ergebnis dieselbe Matrix ergibt.

$A\cdot A = A$

Daher ist jede Potenz einer idempotenten Matrix gleich der Matrix selbst, unabhängig vom Exponenten:

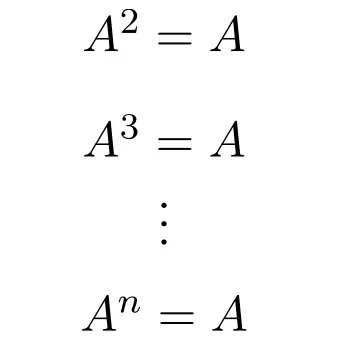
Deshalb hat diese Art von Board auch seinen Namen erhalten. Denn in der Mathematik ist Idempotenz eine Operation, die bedeutet, dass wir immer das gleiche Ergebnis erhalten, unabhängig davon, wie oft sie ausgeführt wird.

Beispiele für idempotente Matrizen

Sobald wir das Konzept der idempotenten Matrix kennen, werden wir einige Beispiele verschiedener Dimensionen sehen, um das Verständnis zu vervollständigen.

Beispiel einer 2×2 idempotenten Matrix

Die folgende quadratische Matrix der Dimension 2×2 ist idempotent:

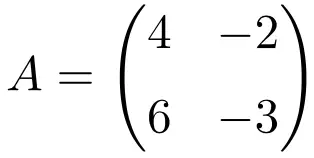
Beispiel einer idempotenten Matrix der Dimension 2x2

Um zu überprüfen, ob es sich um eine idempotente Matrix handelt, berechnen wir ihr Quadrat:

$\displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}$

Das Ergebnis ist identisch, wir zeigen daher, dass es sich um eine idempotente Matrix handelt.

Beispiel einer idempotenten 3×3-Matrix

Die folgende quadratische Matrix der Größe 3×3 ist idempotent:

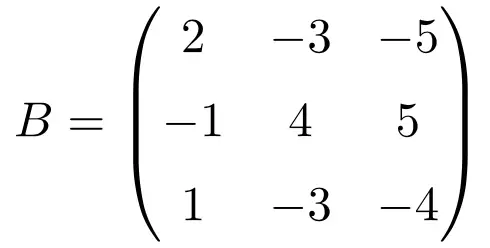
Beispiel einer idempotenten Matrix der Dimension 3x3

Um zu überprüfen, ob eine idempotente Matrix korrespondiert, erhöhen wir die Matrix auf 2:

$\displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}$

Das Ergebnis ist das gleiche wie bei der Originalmatrix, sodass die Idempotenz der Matrix bewiesen ist.

Struktur einer 2×2 idempotenten Matrix

Hier zeigen wir Ihnen die Formel zum Erhalten einer idempotenten Matrix. Falls Sie mehr Interesse haben, können Sie die Demonstration der Formel unten in den Kommentaren sehen, aber sie ist etwas mühsam, deshalb überlassen wir Ihnen hier direkt die Formel für idempotente Matrizen :

Auf diese Weise können die Elemente der Nebendiagonale einer idempotenten Matrix beliebig sein, solange die Bedingung erfüllt ist

$a^2+bc=a$

und die Zahlen auf der Hauptdiagonalen müssen sein

$a$

Und

$1-a.$

Zusätzlich zu allen durch diese Formel beschriebenen Matrizen müssen wir die Identitätsmatrix hinzufügen, die ebenfalls eine idempotente Matrix ist, obwohl sie die Formel nicht respektiert. Wenn Sie das Array nicht kennen, können Sie nach dem Identitätsarray fragen.

Eigenschaften idempotenter Matrizen

Idempotente Matrizen haben die folgenden Eigenschaften:

Die Determinante einer idempotenten Matrix ist immer 0 oder 1.

Mit Ausnahme der Identitätsmatrix sind alle anderen idempotenten Matrizen sowohl singuläre als auch entartete Matrizen, das heißt, sie sind nicht invertierbar.

Jede idempotente Matrix ist diagonalisierbar und ihre Eigenwerte (oder Eigenwerte) sind immer 0 oder 1.

Die Spur einer idempotenten Matrix ist gleich dem Rang der Matrix.

Schließlich gibt es eine Beziehung zwischen idempotenten Matrizen und Involutionsmatrizen: die Matrix
$A$

ist genau dann idempotent, wenn die Matrix

$\displaystyle P= 2A-I$

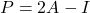
es ist involutionär.