In diesem Abschnitt werden wir alle Eigenschaften von Determinanten sehen. Wir demonstrieren jede Immobilie auch anhand eines Beispiels, damit Sie sie vollständig verstehen. Darüber hinaus finden Sie Übungen zu den Eigenschaften von Determinanten.
Im Folgenden erklären wir jede Eigenschaft der Determinanten einzeln. Wenn Sie möchten, können Sie jedoch direkt zur nachstehenden Übersichtstabelle springen. 😉
Eigenschaft 1: Determinante der transponierten Matrix
Die Determinante einer Matrix entspricht der Determinante ihrer transponierten Matrix.
Beispiel:
![\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e39b73d52e436c660c2c9f2eeed39f6_l3.png "Rendered by QuickLaTeX.com")
Jetzt transponieren wir die 2×2-Matrix und lösen nach der Determinante auf. Beachten Sie, dass wir das gleiche Ergebnis wie zuvor erhalten:
![\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc16abe425fb139cb3a6b7ba7e3b1915_l3.png "Rendered by QuickLaTeX.com")
Eigenschaft 2: Determinante mit einer mit Nullen gefüllten Zeile oder Spalte
Wenn eine Determinante eine Zeile oder Spalte mit Nullen enthält, gibt die Determinante 0 zurück.
![\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-54df933d2167697d926c25dd9554d90a_l3.png "Rendered by QuickLaTeX.com")
Beispiel:
![\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95bc2d762871764f41176acc052a633c_l3.png "Rendered by QuickLaTeX.com")
In beiden Beispielen ergeben die Determinanten den Wert 0. Denn die zweite Zeile der ersten Determinante besteht ausschließlich aus Nullen und die dritte Spalte der zweiten Determinante besteht ebenfalls ausschließlich aus Nullen.
Eigenschaft 3: Determinante mit zwei gleichen Zeilen oder Spalten
Wenn eine Determinante zwei gleiche oder mehrere Zeilen oder zwei Spalten hat, ist die Determinante Null (0).
Wenn es also eine lineare Kombination zwischen Zeilen oder Spalten gibt, das heißt, sie sind linear abhängig, ergibt die Determinante 0.
Beispiel:
![\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c31b59570d4f89e8c7e7aa9f922977c5_l3.png "Rendered by QuickLaTeX.com")
In diesem Fall ergibt die Determinante 0, da die Spalten 2 und 3 gleich sind.
Eigenschaft 4: Ändern Sie die Zeilen oder Spalten einer Determinante
Wenn zwei Zeilen oder zwei Spalten relativ zueinander geändert werden, liefert die Determinante das gleiche Ergebnis, jedoch mit einem anderen Vorzeichen.
![\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-de79fc53e94c9a30d8a271d42d4e3494_l3.png "Rendered by QuickLaTeX.com")
Beispiel:
![\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2e4806318fa67998b339383a9dc9ea5_l3.png "Rendered by QuickLaTeX.com")
Jetzt ändern wir die Reihenfolge der Spalten 2 und 3 relativ zueinander. Beachten Sie, dass das Ergebnis dasselbe ist, jedoch mit einem anderen Vorzeichen:
![\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4a4de8b8cf37df2c3cce69d16a19a578_l3.png "Rendered by QuickLaTeX.com")
Eigenschaft 5: Multiplizieren Sie eine Zeile einer Determinante mit einem Skalar
Die Multiplikation aller Elemente in einer ganzen Zeile oder Spalte mit einer reellen Zahl ist dasselbe wie die Multiplikation des Ergebnisses der Determinante mit dieser Zahl.
![\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06cf5f62a3d703b43bb68b319839df26_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7b38fe06dab0bbdbfef384b3e403fed_l3.png "Rendered by QuickLaTeX.com")
Beispiel:
![\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92b404bb7ad8bbdd59c8c54c1619c37d_l3.png "Rendered by QuickLaTeX.com")
Jetzt nehmen wir dieselbe Determinante und multiplizieren eine ganze Zeile mit 2. Sie werden sehen, dass das Ergebnis das der vorherigen Determinante sein wird, jedoch multipliziert mit 2 oder 10:
![\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}](https://mathority.org/wp-content/ql-cache/quicklatex.com-57ae1ba33c0d108f08ac9d0b5cb4a81b_l3.png "Rendered by QuickLaTeX.com")
Eigenschaft 6: Determinante des Matrixprodukts
Die Determinante des Produkts zweier Matrizen ist gleich dem Produkt der Determinante jeder Matrix einzeln.
Beispiel:
Um diese Eigenschaft von Determinanten zu demonstrieren, berechnen wir die Determinante der Multiplikation der folgenden beiden Matrizen auf zwei mögliche Arten:
![\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38de0ca99ad15f40bd94f653cffacf8d_l3.png "Rendered by QuickLaTeX.com")
Wir multiplizieren zunächst die beiden Matrizen und berechnen dann die Determinante der resultierenden Matrix:
![\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2ad18d1637b581038b7866030d6ac9a0_l3.png "Rendered by QuickLaTeX.com")
Jetzt berechnen wir die Determinante jeder Matrix separat und multiplizieren dann die Ergebnisse:
![\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f7c97d5a832d3985bf1d5e9d4d44401_l3.png "Rendered by QuickLaTeX.com")
Wie Sie sehen können, führt die Berechnung des Matrixprodukts und dann die Bestimmung der Determinante zum gleichen Ergebnis wie die Berechnung der Determinante jeder Matrix und die anschließende Multiplikation der Ergebnisse.
Andererseits gilt diese Bedingung nicht für Additions- und Subtraktionsoperationen, das heißt, dass die Determinante der Addition (oder Subtraktion) zweier Matrizen nicht das gleiche Ergebnis liefert wie die Addition (oder Subtraktion) der Determinanten von zwei Matrizen getrennt.
Eigenschaft 7: Determinante der inversen Matrix
Wenn eine Matrix invertierbar ist, entspricht die Determinante ihrer Umkehrung der Umkehrung der Determinante der ursprünglichen Matrix.
Beispiel:
Wir werden diese Eigenschaft überprüfen, indem wir zunächst die Umkehrung einer Matrix berechnen und dann nach ihrer Determinante auflösen. Wir werden sehen, dass das Ergebnis dem Finden der Determinante der ursprünglichen Matrix und deren Invertierung entspricht.
Wir invertieren daher die folgende Matrix und berechnen ihre Determinante:
![\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c77c10006d35ebc5273553fb84356e3_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a9315a8add365cd5f077c52476a827d_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a10c873ff6c101cd2b239388393c268b_l3.png "Rendered by QuickLaTeX.com")
Und jetzt lösen wir nach der Determinante der ursprünglichen Matrix und machen ihre Umkehrung:
![\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-850e5404f5352782327918caab3e1440_l3.png "Rendered by QuickLaTeX.com")
Wie Sie sehen, sind die Ergebnisse beider Operationen identisch. Die Eigenschaft ist somit nachgewiesen.
Eigenschaft 8: Ersetzen Sie die Zeile eines Bestimmers
Die Zeile einer Determinante kann ersetzt werden, indem dieselbe Zeile plus (oder minus) einer anderen Zeile multipliziert mit einer Zahl addiert (oder subtrahiert) wird.
Beispiel:
Mit dem folgenden Beispiel überprüfen wir diese Eigenschaft. Wir berechnen zunächst eine Determinante, bearbeiten dann eine Zeile der Determinante und berechnen ihr Ergebnis neu. Sie werden sehen, dass wir in beiden Fällen zum gleichen Ergebnis kommen.
Berechnen wir also zunächst eine 3×3-Determinante mit der Sarrus-Regel:
![\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ccd76fc3a2b7cd7afc7d8f9de8ffde1_l3.png "Rendered by QuickLaTeX.com")
Nun addieren wir in Zeile 2 die erste Zeile multipliziert mit 2:
![\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4bc2e6bd78446fb68f29b4a5503a6828_l3.png "Rendered by QuickLaTeX.com")
Und wir lösen die Determinante, nachdem wir eine ihrer Geraden transformiert haben:
![\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-045eb6f32420fbbf538a9e0a540ce119_l3.png "Rendered by QuickLaTeX.com")
In beiden Fällen war das Ergebnis -3. Somit wird gezeigt, dass sich das Ergebnis einer Determinante nicht ändert, wenn eine Zeile durch die Summe derselben Zeile plus einer anderen Zeile multipliziert mit einer Zahl ersetzt wird.
Eigenschaft 9: Determinante einer Dreiecksmatrix
Die Determinante einer Dreiecksmatrix ist das Produkt der Elemente ihrer Hauptdiagonale.
Beispiel:
Als Beispiel lösen wir die Determinante der folgenden Dreiecksmatrix:
![\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}](https://mathority.org/wp-content/ql-cache/quicklatex.com-40ebfa5f9f06e63ad1325d9331a57bde_l3.png "Rendered by QuickLaTeX.com")
Eigenschaft 10: Determinante einer Diagonalmatrix
Die Determinante einer Diagonalmatrix ist gleich der Multiplikation der Elemente ihrer Hauptdiagonale.
Beispiel:
Nehmen wir als Beispiel die Determinante der folgenden Diagonalmatrix:
![\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56e1b3093685a1af729310752b03dfc9_l3.png "Rendered by QuickLaTeX.com")
Zusammenfassende Tabelle der Eigenschaften von Determinanten
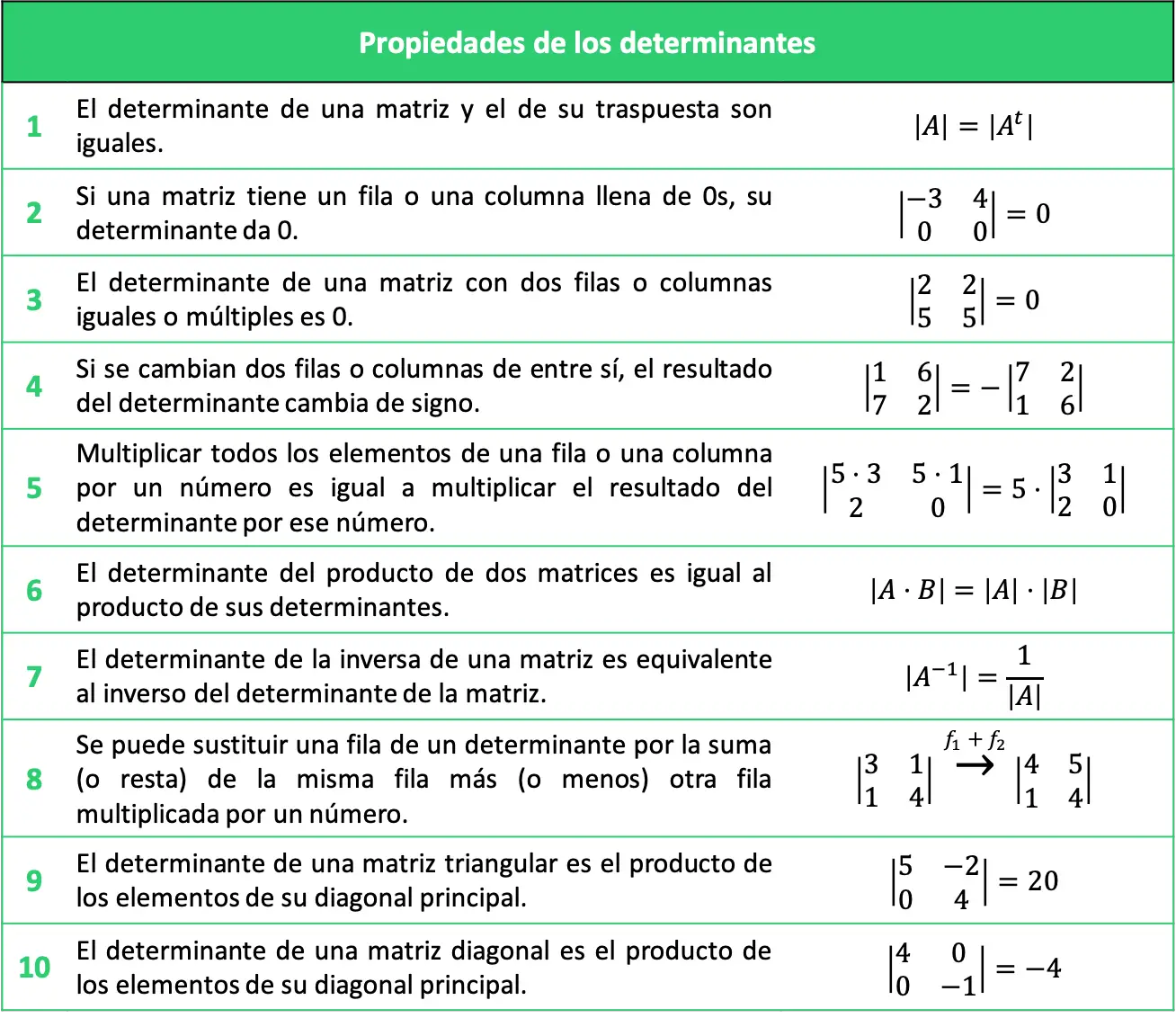
Die Eigenschaften der erläuterten Determinanten lassen sich in der folgenden Tabelle zusammenfassen:
Gelöste Aufgaben zu den Eigenschaften von Determinanten
Übung 1
Lösen Sie die folgende Determinante:
![\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-97dfc1ebfc5db73750870911108bd447_l3.png "Rendered by QuickLaTeX.com")
Wenn eine Determinante eine Zeile oder Spalte mit Nullen enthält, gibt die Determinante 0 zurück (Eigenschaft 2). Daher ist das Ergebnis der Determinante 0, da die dritte Spalte mit Nullen gefüllt ist.
Übung 2
Lösen Sie die folgende Determinante:
![\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdb315ba588fe5fdfb03c7fea2857b16_l3.png "Rendered by QuickLaTeX.com")
Wenn eine Determinante zwei gleiche oder mehrere Zeilen oder zwei Spalten hat, gibt die Determinante 0 zurück (Eigenschaft 3). Daher ist das Ergebnis der Determinante 0, da die erste Zeile und die dritte Zeile gleich sind.
Übung 3
Berechnen Sie die folgende Determinante:
![\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96c5cfee4c4189e49b54fdf43b2a0457_l3.png "Rendered by QuickLaTeX.com")
Wenn eine Determinante zwei gleiche oder mehrere Zeilen oder zwei Spalten hat, gibt die Determinante 0 zurück (Eigenschaft 3). Daher ist das Ergebnis der Determinante 0, da die vierte Spalte doppelt so groß ist wie die erste Spalte.
Übung 4
Wir kennen das Ergebnis einer Determinante, obwohl wir die Elemente der Matrix nicht kennen:
![\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-e20d9016edd52f18d3ffc928d2658efe_l3.png "Rendered by QuickLaTeX.com")
Berechnen Sie aus dem Ergebnis der vorherigen Determinante und den Eigenschaften der Determinanten das Ergebnis der folgenden Determinanten:
![\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c20de8d82171dc8fb784e2549521f37_l3.png "Rendered by QuickLaTeX.com")
Für)
ist die transponierte Matrix von
. Und die Determinante einer Matrix ist gleich der Determinante ihrer transponierten Matrix (Eigenschaft 1). Daher ist das Ergebnis dieser Determinante auch 3.
![\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bf7ae0a2ff32d75a6f7abafb623639c_l3.png "Rendered by QuickLaTeX.com")
b) In der Bestimmung
Die Spalten 1 und 2 wurden hinsichtlich des Bestimmers der Anweisung geändert
. Daher ist das Ergebnis gemäß Eigenschaft 4 dasselbe wie das Ergebnis des Bestimmers der Aussage, jedoch mit einem anderen Vorzeichen, nämlich -3.
![\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6d14aa2f6b8c7d1fd064daef8dd0eec_l3.png "Rendered by QuickLaTeX.com")
c) In der Bestimmung
Die gesamte zweite Spalte der Determinante der Aussage wurde mit 3 multipliziert. Daher können wir aus Eigenschaft 5 ableiten, dass ihr Ergebnis auch das Ergebnis der Determinante der Aussage multipliziert mit 3, also 9, sein wird.
![\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1a7ffec429367a2fd967a197d0299d2_l3.png "Rendered by QuickLaTeX.com")
Übung 5
Wir kennen das Ergebnis dieser beiden Determinanten:
![\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8](https://mathority.org/wp-content/ql-cache/quicklatex.com-e938c40ce401263da9835fa77fc9a1dd_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4](https://mathority.org/wp-content/ql-cache/quicklatex.com-6cea0d73e66099f2a10f71f7267baee9_l3.png "Rendered by QuickLaTeX.com")
Berechnen Sie aus diesen Informationen:
Um das Ergebnis der Determinante zu berechnen, ist es nicht notwendig, 4×4-Matrizen zu multiplizieren. Da die Determinante des Produkts zweier Matrizen gleich dem Produkt der Determinante jeder Matrix einzeln ist (Eigenschaft 6). Noch:
