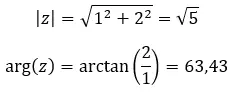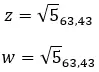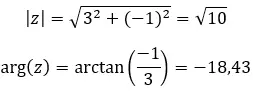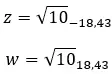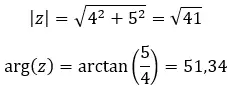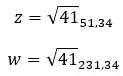In diesem Artikel besprechen wir die Eigenschaften komplexer Zahlen , die beim Lösen von Berechnungen und beim Vereinfachen von Ausdrücken nützlich sein können. Kommen wir gleich zu diesen Eigenschaften.
Modul und Argument einer komplexen Zahl
Die erste Eigenschaft einer komplexen Zahl ist der Modul und das Argument einer komplexen Zahl. Die Berechnung ist sehr einfach, da Sie nur ein paar Formeln anwenden müssen.
Die Formel zur Berechnung des Moduls:

Die Formel zur Berechnung des Arguments:

Wenn die Zahl nun in polarer oder trigonometrischer Form ausgedrückt wird, sind keine Berechnungen erforderlich. Denn im gleichen Ausdruck werden Modul und Argument aufgelistet.
Im Bild unten sehen Sie die Formel für eine Zahl in Polarform, wobei |z| ist der Modul und α ist das Argument.

Und in diesem anderen Bild können Sie die Struktur einer Zahl in trigonometrischer Form sehen, wobei |z| ist der Modul und α ist das Argument.

gleiche komplexe Zahlen
Gleiche komplexe Zahlen sind solche, die Modul und Argument gemeinsam haben. Also, aus diesen beiden Werten:

Diese sind gleich, wenn die folgende Eigenschaft erfüllt ist.
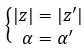
Wenn wir andererseits beide Zahlen in Binomialform haben, können wir sehr schnell und einfach überprüfen, ob es sich um zwei gleiche komplexe Zahlen handelt. Einfach gesagt muss der folgende Ausdruck erfüllt sein:
a + bi = a + bi
Sehen wir uns ein Beispiel an, um festzustellen, ob die folgenden zwei komplexen Zahlen gleich sind:
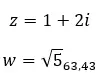
Komplexe Zahlen konjugieren
Kommen wir nun zu einer der wichtigsten Eigenschaften komplexer Zahlen, denn zu wissen, wie man das Konjugierte eines Komplexes berechnet, hilft uns sehr beim Lösen komplexer Divisionen und beim Vornehmen von Vereinfachungen.
Also, aus diesen beiden Werten:

Wir sagen, dass sie konjugiert sind, wenn sie ein gemeinsames Modul haben und gegensätzliche Argumente haben. Es muss daher ausgefüllt werden:
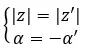
Wenn wir andererseits beide Zahlen in Binomialform haben, können wir sehr schnell und einfach überprüfen, ob es sich um zwei komplex konjugierte Zahlen handelt. Einfach gesagt muss der folgende Ausdruck erfüllt sein:
un + bi = un – bi
Sehen wir uns ein Beispiel an, um festzustellen, ob die folgenden zwei komplexen Zahlen konjugiert sind:
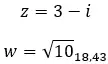
Gegenteilige komplexe Zahlen
Als nächstes betrachten wir die Eigenschaft entgegengesetzter komplexer Zahlen. Aus diesen beiden Werten:

Wir können sagen, dass sie Gegensätze sind, wenn sie denselben Modul haben und sich ihre Argumente um 180 Grad oder π im Bogenmaß unterscheiden:
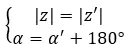
Wenn wir hingegen beide Zahlen in Binomialform haben, können wir eine andere, noch schnellere und einfachere Methode verwenden, um herauszufinden, ob es sich um zwei entgegengesetzte komplexe Zahlen handelt. Einfach gesagt muss der folgende Ausdruck erfüllt sein:
a + bi = -a – bi
Sehen wir uns ein Beispiel an, um festzustellen, ob die folgenden zwei komplexen Zahlen entgegengesetzt sind:
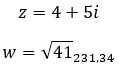
andere Eigenschaften
Offensichtlich verfügt dieser Zahlensatz über weitere Eigenschaften, wie z. B. inverse komplexe Zahlen und einige andere, die in direktem Zusammenhang mit grundlegenden arithmetischen Operationen stehen. All dies wird jedoch in anderen Artikeln behandelt, die Sie in der Liste unten sehen können.
Erfahren Sie mehr über die Eigenschaften komplexer Zahlen
- Komplexe Zahlen
- Operationen mit komplexen Zahlen
- komplexe Wurzeln
- Grafische Darstellung komplexer Zahlen