Auf dieser Seite erklären wir, was eine kombinatorische Zahl ist und wie sie berechnet wird (Formel). Darüber hinaus können Sie Beispiele für die Berechnung beliebiger kombinatorischer Zahlen sehen und anhand von Schritt-für-Schritt-Übungen üben. Wir zeigen auch alle Eigenschaften und Anwendungen kombinatorischer Zahlen. Und schließlich lernen wir, wie man das Ergebnis einer kombinatorischen Zahl direkt mit dem Taschenrechner ermittelt.
Was ist eine kombinatorische Zahl?
In der Mathematik ist die kombinatorische Zahl , auch Binomialkoeffizient genannt, die Anzahl gewöhnlicher Kombinationen (Kombinationen ohne Wiederholung) von Gruppen von k Elementen, die aus einer Menge von n Elementen (n>k) gebildet werden können.
Eine kombinatorische Zahl wird in Klammern wie folgt ausgedrückt:
![]()
Andererseits wird die kombinatorische Zahl n über k gelesen. Ebenso wird n als Zähler und k als Ordnung bezeichnet.
Allein mit der Definition einer kombinatorischen Zahl ist es schwierig, ihre Bedeutung zu verstehen. Wir werden nun jedoch sehen, wie die kombinatorische Zahl mathematisch ermittelt wird, und dann tiefer in dieses Konzept der Kombinatorik eintauchen. Sie werden sehen, dass Sie es so besser verstehen werden.
Kombinatorische Zahlenformel
Die Formel zur Berechnung des Wertes einer kombinatorischen Zahl (oder eines Binomialkoeffizienten) lautet wie folgt:
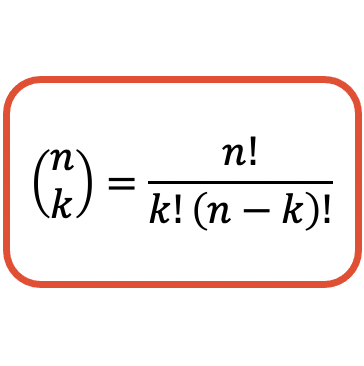
Denken Sie daran, dass in der Algebra das Ausrufezeichen der Fakultät einer Zahl entspricht. Und um die Fakultät einer Zahl zu ermitteln, müssen Sie alle positiven ganzen Zahlen von 1 mit dieser Zahl multiplizieren. Um beispielsweise die Fakultät der Zahl 4 zu berechnen, müssen Sie 1, 2, 3 und 4 multiplizieren:
![]()
Es ist auch wichtig, dass Sie wissen, dass die Fakultät von 0 gleich 1 ist.
![]()
Beispiel für die Berechnung einer kombinatorischen Zahl
Als nächstes ermitteln wir beispielhaft Schritt für Schritt den Wert einer kombinatorischen Zahl, damit Sie sehen können, wie es geht:
- Berechnen Sie den Wert der kombinatorischen Zahl 5 über 3.
Der Binomialkoeffizient von 5 über 3 entspricht dem folgenden Ausdruck:
![]()
Wenn wir also die Formel für kombinatorische Zahlen anwenden, müssen wir zur Bestimmung ihres Wertes die folgenden Operationen durchführen:
![]()
Oder gleichwertig:
![]()
Wir finden daher die Fakultäten:
![]()
Die Multiplikation 1·2·3 wird im Zähler und Nenner wiederholt, sodass der Bruch durch Eliminierung dieses Faktors vereinfacht werden kann:
![]()
![]()
Jetzt berechnen wir die Produkte:
![]()
Und schließlich nehmen wir die Aufteilung vor:
![]()
Eigenschaften der kombinatorischen Zahl
Kombinatorische Zahlen oder Binomialkoeffizienten können gemäß den folgenden Eigenschaften kombiniert werden:
- Zwei komplementäre kombinatorische Zahlen sind solche, die den gleichen Zähler n haben und die Summe ihrer Ordnungen diesem Zähler entspricht. Somit ist das Ergebnis zweier komplementärer kombinatorischer Zahlen identisch.
![]()
Dieses Merkmal kombinatorischer Zahlen wird auch Symmetrieidentität genannt.
Beispielsweise ergibt 6 über 4 das gleiche Ergebnis wie 6 über 2, weil 6-4=2.
![]()
![]()
- Die Summe zweier kombinatorischer Zahlen mit demselben Zähler und aufeinanderfolgenden Ordnungen ist gleich einer anderen kombinatorischen Zahl, deren Zähler dem Zähler der Additionen plus 1 entspricht und deren Ordnung dem größten Wert der Ordnungen der Additionen entspricht. Mit anderen Worten, die folgende Bedingung ist immer erfüllt:
![]()
Zum Beispiel:
![]()
Diese Eigenschaft wird auch als Pascal-Regel bezeichnet.
Andererseits kann diese Formel auch umgekehrt angewendet werden, um eine kombinatorische Zahl in zwei einfachere kombinatorische Zahlen zu zerlegen:
![]()
Beispielsweise ist die kombinatorische Zahl 8 über 4 gleich 7 über 3 plus 7 über 4:
![]()
- Jede positive Zahl größer als 1 ist gleich der Zahl selbst.
![]()
Der Grund für diese Eigenschaft liegt darin, dass die Fakultät einer Zahl gleich der Fakultät der vorherigen Zahl multipliziert mit der Zahl selbst ist:
![]()
Beispiele für diese Art von kombinatorischen Zahlen:
![]()
- Jede positive Zahl größer als 0 ist gleich eins.
![]()
Tatsächlich ist der Nenner des Bruchs einer solchen kombinatorischen Zahl immer gleich dem Zähler des Bruchs:
![]()
Beispiele für kombinatorische Zahlen wie diese:
![]()
- Jede Zahl für sich ist gleich 1.
![]()
Hier ist die Demo:
![]()
Beispiele für kombinatorische Zahlen wie diese:
![]()
So berechnen Sie eine kombinatorische Zahl mit dem Taschenrechner
Bisher haben wir gesehen, wie man eine kombinatorische Zahl aus mehr oder weniger einfachen Zahlen ermittelt. Wenn wir jedoch mit sehr großen Mengen arbeiten müssen, ist es besser, den Taschenrechner zur Bestimmung der kombinatorischen Zahl zu verwenden. Wir werden nun sehen, wie man eine kombinatorische Zahl in den Rechner eingibt.
Der Schlüssel, der zum Berechnen einer kombinatorischen Zahl mit dem Taschenrechner verwendet wird, ist also der Schlüssel nCr . Und um den Wert der kombinatorischen Zahl zu bestimmen, müssen Sie zuerst den Zähler der kombinatorischen Zahl eingeben, zweitens die Taste nCr drücken, dann die Reihenfolge der kombinatorischen Zahl eingeben und schließlich die Taste „Gleich“ drücken.
![]()
Bei wissenschaftlichen Taschenrechnern von CASIO verfügt die nCr-Taste je nach Modell meist über eine eigene Taste oder befindet sich oberhalb der Divisionstaste.
Wenn wir beispielsweise wissen möchten, wie hoch die kombinatorische Zahl 10 über 6 ist, müssen wir die folgende Sequenz ausführen:
![]()
Anwendungen der kombinatorischen Zahl
Wenn Sie es bis hierher geschafft haben, wissen Sie wahrscheinlich bereits, wie man jede kombinatorische Zahl perfekt löst. Aber… wofür wird die kombinatorische Zahl verwendet? Dann werden wir alle Vorteile sehen, die diese Art von ganz besonderem Eingriff mit sich bringt.
Kombinatorik
Wie wir oben auf der Seite gesehen haben, ist das Ergebnis einer kombinatorischen Zahl
![]()
stellt die Anzahl der möglichen Gruppen dar
![]()
Elemente, die aus einer Menge von insgesamt gebildet werden können
![]()
Artikel.
Daher können einige kombinatorische Probleme mithilfe kombinatorischer Zahlen (oder Binomialkoeffizienten) gelöst werden. Sehen wir uns anhand eines Beispiels an, wie das geht:
- In einer Klasse mit 30 Schülern wollen wir eine Gruppe von 4 Schülern für die Bearbeitung bestimmter Aufgaben auswählen. Wie viele verschiedene Gruppen können insgesamt gebildet werden?
In diesem Fall spielt die Reihenfolge der Schüler keine Rolle, derselbe Schüler wiederholt sich nicht zweimal innerhalb der Gruppe und nicht alle Schüler kommen in die Gruppe. Daher kann die kombinatorische Zahlenformel verwendet werden, um zu bestimmen, auf wie viele Arten die Gruppe gebildet werden kann.
Dazu müssen Sie die kombinatorische Zahl mit der Gesamtzahl der Studierenden als Zähler und mit der Anzahl der Studierenden, die die Gruppe bilden werden, als Reihenfolge berechnen:
![]()
Die Gesamtzahl der möglichen Kombinationen beträgt somit 27.405 Gruppen.
Newtons Binomial
Eine weitere Anwendung kombinatorischer Zahlen ist das Newtonsche Binomial. Newtons Binomial ist ein Polynom, das aus zwei Termen besteht, die zu einer ganzen Zahl zusammengefasst werden. Das heißt, dass Newtons Binomial das Polynom ist, das auf den folgenden algebraischen Ausdruck reagiert:
![]()
Wenn das Binomial quadriert wird, bedeutet dies natürlich, dass es sich um eine bemerkenswerte Identität handelt und daher leicht mit der entsprechenden Formel berechnet werden kann. Wenn andererseits das Binomial auf große Zahlen erhöht wird, wird die Berechnung ziemlich schwierig. Nun, Newtons Binomialsatz besagt, dass diese Art von Polynomen sehr einfach aus kombinatorischen Zahlen berechnet werden kann.
Klicken Sie auf den folgenden Link und erfahren Sie, was Newtons Binomialformel ist und wie sie berechnet wird. Darüber hinaus können Sie Beispiele sehen und mit Schritt für Schritt gelösten Übungen üben. Und schließlich werden Sie die merkwürdige Geschichte dieses Theorems entdecken.
Tartaglias (oder Pascals) Dreieck
Wie Sie in diesem Artikel gesehen haben, kann die manuelle Berechnung des Binomialkoeffizienten großer Zahlen mühsam und kompliziert sein.
Beim Tartaglia-Dreieck, auch Pascal-Dreieck genannt, lassen sich hingegen alle kombinatorischen Zahlen einfach mithilfe einer Gedächtnisregel ermitteln. Dies ist logischerweise sehr nützlich, da es bei den Berechnungen viel Zeit spart.
Wie das genau geht, erfahren Sie in der Dreieckserklärung von Tartaglia . Auf dieser verlinkten Seite erfahren Sie, was dieses geheimnisvolle Dreieck ist, wofür es verwendet wird (es hat überraschende Anwendungen) 😮 und wo sein Ursprung liegt (es wurde bereits vor mehr als 1000 Jahren verwendet).
Aufgaben zu kombinatorischen Zahlen gelöst
Damit Sie die erläuterten Konzepte üben und vollständig verstehen können, überlassen wir Ihnen einige Schritt-für-Schritt-Übungen zu kombinatorischen Zahlen.
Übung 1
Finden Sie die kombinatorische Zahl 9 mal 5 (ohne einen Taschenrechner zu verwenden).
Um den Wert der kombinatorischen Zahl 9 aus 5 zu ermitteln, wenden wir einfach die Fakultätsformel an:
![]()
Übung 2
Was ist das Ergebnis der folgenden Summe zweier kombinatorischer Zahlen? (ohne Taschenrechner)
![]()
Aus den Eigenschaften kombinatorischer Zahlen folgt, dass die Summe des Problems gleich der folgenden kombinatorischen Zahl ist:
![]()
Daher reicht es aus, die kombinatorische Zahl 11 aus 7 zu berechnen:
![]()
Übung 3
Bestimmen Sie, ob die folgenden kombinatorischen Zahlen gleich sind:
![]()
Um das Ergebnis der drei kombinatorischen Zahlen zu ermitteln, müssen Sie keinen Taschenrechner verwenden, sie können jedoch dank der Eigenschaften kombinatorischer Zahlen leicht ermittelt werden.
Zunächst einmal ergibt eine kombinatorische Zahl einer beliebigen Zahl größer als 1 1. Daher:
![]()
Andererseits ist jede Zahl größer als eins gleich der Zahl selbst. Noch:
![]()
Und schließlich ist jede kombinatorische Zahl, die aus derselben Zahl besteht, die zweimal wiederholt wird, äquivalent zu 1. Also:
![]()
Zusammenfassend lässt sich sagen, dass die erste und dritte kombinatorische Zahl im Problem gleich sind, sich jedoch von der mittleren kombinatorischen Zahl unterscheiden.
![]()