Auf dieser Seite finden Sie die Formeln für alle Gleichungen im Plan und wie sie berechnet werden. Außerdem erfahren Sie, wie Sie die Gleichung einer beliebigen Ebene mit ihrem Normalenvektor finden. Darüber hinaus können Sie Beispiele sehen und mit gelösten Übungen die Gleichungen des Plans üben.
Wie lautet die Gleichung der Ebene?
In der analytischen Geometrie ist die Gleichung einer Ebene eine Gleichung, die es ermöglicht, jede Ebene mathematisch auszudrücken. Um die Gleichung einer Ebene zu finden, benötigen Sie also nur einen Punkt und zwei linear unabhängige Vektoren, die zu dieser Ebene gehören.
Bevor Sie mit der Erklärung von Ebenengleichungen fortfahren, müssen Sie unbedingt verstehen, was Ebene (Geometrie) ist, da es sonst Dinge gibt, die Sie nicht verstehen. Wenn Sie sich nicht ganz sicher sind, können Sie es unter diesem Link nachlesen. Dort haben wir alles zusammengefasst, was Sie über den Plan wissen müssen.
Was sind die Gleichungen des Plans?
Wie wir bei der Definition der Gleichung einer Ebene gesehen haben, kann jeder Punkt auf einer flachen Ebene als lineare Kombination aus einem Punkt und zwei Vektoren ausgedrückt werden.

Eine notwendige Bedingung dafür, dass die Gleichung einer Ebene entspricht, ist jedoch, dass die beiden Vektoren der Ebene lineare Unabhängigkeit haben, das heißt, die beiden Vektoren können nicht parallel zueinander sein.
Somit sind alle Arten von Gleichungen der Ebene: die Vektorgleichung , die parametrischen Gleichungen , die implizite (oder allgemeine) Gleichung und die kanonische (oder segmentale) Gleichung der Ebene.
Dann werden wir die Erklärung und Formel aller Gleichungen des Plans im Detail sehen.
Vektorgleichung der Ebene
Betrachten Sie einen Punkt und zwei Richtungsvektoren einer Ebene:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Die Formel für die Vektorgleichung einer Ebene lautet:
![]()
Oder gleichwertig:
![]()
Gold
![]()
Und
![]()
sind zwei Skalare, also zwei reelle Zahlen.
Parametrische Gleichungen der Ebene
Die Parametergleichung einer Ebene kann aus ihrer Vektorgleichung bestimmt werden. Unten können Sie die Demo sehen.
Die Vektorgleichung einer beliebigen Ebene sei:
![]()
Wir operieren und führen zunächst die Produkte von Vektoren durch die Skalare aus:
![]()
Als nächstes fügen wir die Komponenten hinzu:
![]()
Und schließlich erhalten wir die parametrischen Gleichungen des Plans, indem wir die Koordinaten, die jeder Variablen entsprechen, separat assimilieren:
![]()
Gold:
-
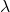
Und
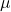
sind zwei Skalare, also zwei reelle Zahlen.
-
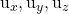
sind die Komponenten eines der beiden Leitvektoren des Plans
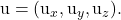
-
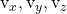
sind die Komponenten des anderen Richtungsvektors des Plans
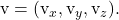
Implizite oder allgemeine Gleichung der Ebene
Betrachten Sie einen Punkt und zwei Richtungsvektoren einer Ebene:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Die implizite, allgemeine oder kartesische Gleichung einer Ebene erhält man, indem man die folgende Determinante löst und das Ergebnis gleich 0 setzt:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Somit lautet die implizite oder allgemeine Gleichung des resultierenden Plans wie folgt:
![]()
Diese Art der Ebenengleichung wird auch als kartesische Ebenengleichung bezeichnet.
Kanonische oder segmentale Gleichung der Ebene
Die Formel für die kanonische oder segmentale Gleichung einer Ebene lautet wie folgt:
![]()
Gold:
-

ist der Schnittpunkt zwischen der Ebene und der X-Achse.
-

ist der Schnittpunkt zwischen der Ebene und der Y-Achse.
-

Hier schneidet die Ebene die Z-Achse.
Die kanonische Gleichung (oder Segmentgleichung) der Ebene kann auch aus ihrer allgemeinen Gleichung erhalten werden:
![]()
Zuerst lösen wir den Koeffizienten D aus der Gleichung:
![]()
Dann dividieren wir die gesamte Plangleichung durch den Wert des Parameters D mit geändertem Vorzeichen:
![]()
![]()
Und wenn wir die Eigenschaften von Brüchen nutzen, kommen wir zu folgendem Ausdruck:
![]()
Aus diesem Ausdruck leiten wir daher die Formeln ab, mit denen sich die Terme der kanonischen oder Segmentgleichung einer Ebene direkt berechnen lassen:
![]()
Um diese Variante der Plangleichungen bilden zu können, müssen daher die Koeffizienten A, B und C von Null verschieden sein, um so Unbestimmtheiten der Brüche zu vermeiden.
So berechnen Sie die Gleichung einer Ebene aus ihrem Normalenvektor
Ein sehr typisches Problem bei Gleichungen einer Ebene besteht darin, herauszufinden, wie die Gleichung einer bestimmten Ebene angesichts eines Punktes und seines Normalen- (oder Senkrechten) Vektors aussieht. Schauen wir uns also an, wie es funktioniert.
Aber Sie müssen zunächst wissen, dass die Komponenten X, Y, Z des Vektors normal zu einer Ebene jeweils mit den Koeffizienten A, B, C der impliziten (oder allgemeinen) Gleichung dieser Ebene übereinstimmen.
![]()
Gold
![]()
ist der Vektor orthogonal zur Ebene
![]()
Sobald wir die vorherige Beziehung kennen, sehen wir uns ein Beispiel für die Lösung dieser Art von Ebenengleichungsproblemen an:
- Bestimmen Sie die implizite oder allgemeine Gleichung der Ebene, die durch den Punkt verläuft
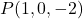
und einer seiner Normalenvektoren ist
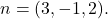
Die Formel für die implizite, allgemeine oder kartesische Gleichung einer Ebene lautet:
![]()
Aus dem Normalenvektor können wir also die Koeffizienten A, B und C ermitteln, da sie den Komponenten seines Normalenvektors entsprechen:
![]()
Dabei müssen wir nur den Parameter D finden. Dazu setzen wir die Koordinaten des Punktes, der zur Ebene gehört, in die Gleichung ein:
![]()
![]()
![]()
![]()
![]()
Die implizite oder allgemeine Gleichung des Plans lautet also:
![]()
Probleme mit Ebenengleichungen gelöst
Übung 1
Bestimmen Sie die Vektorgleichung der Ebene, die den Vektor enthält
![]()
und geht dabei die folgenden zwei Punkte durch:
![]()
Und
![]()
Um die Gleichung einer Ebene zu kennen, braucht man einen Punkt und zwei Vektoren und in diesem Fall haben wir nur einen Vektor, wir müssen also einen anderen Richtungsvektor der Ebene finden. Dazu können wir den Vektor berechnen, der die beiden Punkte der Ebene definiert:
![]()
Da wir nun bereits zwei Richtungsvektoren der Ebene und eines Punktes kennen, verwenden wir daher die Formel für die Vektorgleichung der Ebene:
![]()
Und wir setzen die beiden Vektoren und einen der beiden Punkte auf der Ebene in die Gleichung ein:
![]()
Übung 2
Finden Sie die parametrischen Gleichungen der Ebene, die die folgenden drei Punkte enthält:
![]()
Um die parametrischen Gleichungen der Ebene zu finden, müssen wir zwei linear unabhängige Vektoren finden, die in der Ebene miteinander verbunden sind. Und dazu können wir zwei Vektoren berechnen, die durch die 3 Punkte definiert werden:
![]()
![]()
Die Koordinaten der beiden gefundenen Vektoren sind nicht proportional, also linear unabhängig voneinander.
Da wir nun bereits zwei Richtungsvektoren und einen Punkt auf der Ebene kennen, wenden wir die Formel für die Parametergleichung der Ebene an:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
Und wir setzen die beiden Vektoren und einen der drei Punkte der Ebene in die Gleichung ein:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Übung 3
Finden Sie die implizite oder allgemeine Gleichung der Ebene, die durch den Punkt verläuft
![]()
und enthält die Vektoren
![]()
Und
![]()
Um die allgemeine oder implizite Gleichung der Ebene zu berechnen, muss die folgende Determinante gelöst werden, die aus den beiden Vektoren, den drei Variablen und den Koordinaten des Punktes besteht:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
Also ersetzen wir die Vektoren und den Punkt in der Formel:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
Und nun lösen wir die Determinante der 3×3-Matrix mit der Methode Ihrer Wahl:
![]()
Abschließend führen wir die Operationen durch und gruppieren ähnliche Begriffe:
![]()
![]()
![]()
Die implizite oder allgemeine Gleichung des Plans lautet also:
![]()
Übung 4
Bestimmen Sie, ob der Punkt
![]()
gehört zu folgendem Plan:
![]()
Damit der Punkt in der Ebene liegt, muss seine Gleichung überprüft werden. Daher müssen wir die kartesischen Koordinaten des Punktes in die Gleichung der Ebene einsetzen und prüfen, ob die Gleichung erfüllt ist:
![]()
![]()
![]()
![]()
![]()
Der Punkt respektiert nicht die Gleichung der Ebene und ist daher nicht Teil dieser Ebene.
Übung 5
Finden Sie die Segmentgleichung der Ebene, deren allgemeine (oder implizite) Gleichung lautet:
![]()
Zuerst löschen wir den unabhängigen Term aus der Gleichung:
![]()
Dann dividieren wir die gesamte Plangleichung durch den Wert des Koeffizienten D mit geändertem Vorzeichen:
![]()
![]()
Und wenn wir die Eigenschaften von Brüchen nutzen, kommen wir zu folgendem Ausdruck:
![]()
Die segmentale (oder kanonische) Gleichung der Ebene lautet also:
![]()
Übung 6
Berechnet die implizite oder allgemeine Gleichung der Raumebene, die durch den Punkt verläuft
![]()
und einer seiner Normalenvektoren ist
![]()
Die Formel für die implizite, allgemeine oder kartesische Gleichung einer Ebene lautet:
![]()
Nun, aus dem Normalenvektor können wir die Koeffizienten A, B und C ermitteln, weil sie jeweils gleich den Komponenten des Normalenvektors sind:
![]()
Wir müssen also nur den Parameter D finden. Dazu setzen wir die Koordinaten des Punktes, der zur Ebene gehört, in die Gleichung ein:
![]()
![]()
![]()
![]()
![]()
Zusammenfassend lautet die implizite oder allgemeine Gleichung des Plans:
![]()
Übung 7
Finden Sie die parametrischen Gleichungen der Ebene, die die Linie enthält
![]()
und ist parallel zur rechten Seite
![]()
sind die Zeilen:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Um die parametrischen Gleichungen der Ebene zu finden, müssen wir zwei Richtungsvektoren und einen Punkt auf der Ebene kennen. Die Deklaration sagt uns, dass sie die Zeile enthält
![]()
Daher können wir den Richtungsvektor und einen Punkt auf dieser Linie nehmen, um die Ebene zu definieren. Darüber hinaus sagt uns die Aussage, dass die Ebene parallel zur Geraden ist
![]()
wir können also auch den Richtungsvektor dieser Geraden für die Ebenengleichung verwenden.
das Recht
![]()
wird in Form parametrischer Gleichungen ausgedrückt, sodass die Komponenten seines Richtungsvektors die Koeffizienten der Parameterterme sind
![]()
![]()
Und die kartesischen Koordinaten eines Punktes auf derselben Linie sind die unabhängigen Terme der parametrischen Gleichungen:
![]()
Andererseits die gerade Linie
![]()
hat die Form einer kontinuierlichen Gleichung, so dass die Komponenten ihres Richtungsvektors die Nenner der Brüche sind:
![]()
Daher lauten die parametrischen Gleichungen des Plans:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)