Auf dieser Seite finden Sie eine Erklärung, was eine Ebene ist, wie sie berechnet wird und welche Eigenschaften sie hat. Darüber hinaus können Sie Beispiele für Ebenen sehen, wie die relativen Positionen zwischen zwei Ebenen sind, wie man den Winkel zwischen zwei Ebenen bestimmt und schließlich, wie man jede Ebene mithilfe der Ebenengleichungen numerisch ausdrückt.
Was ist ein Plan?
In der analytischen Geometrie lautet die Definition der Ebene wie folgt:
Eine Ebene ist ein geometrisches Objekt mit zwei Dimensionen (Länge und Breite).
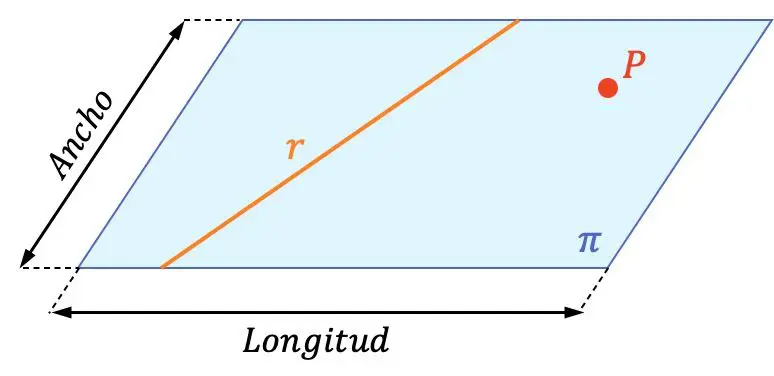
Daher enthält eine Ebene unendlich viele Linien und unendlich viele Punkte. In der grafischen Darstellung oben können Sie den Unterschied zwischen einer Ebene, einer Linie und einem Punkt erkennen. Sie können auch überprüfen, ob die Leitung vorhanden ist
![]()
und der Tipp
![]()
sind im Flugzeug enthalten
![]()
Wie Sie im grafischen Plan sehen können, werden Pläne normalerweise mit griechischen Buchstaben benannt:
![]()
Ein Beispiel für eine Ebene, die wir in der Mathematik häufig verwenden, ist die kartesische Ebene. Die kartesische Ebene ist die Ebene, die durch die Abszissenachse (X-Achse) und die Ordinatenachse (Y-Achse) definiert wird. Die kartesische Ebene wird unter anderem dazu verwendet, die Position eines Objekts in einem Referenzsystem zu beschreiben.
Festlegung eines Plans
Nachdem wir nun die Bedeutung einer Ebene gesehen haben, wollen wir sehen, wie jede beliebige Ebene im dreidimensionalen Raum (in R3) bestimmt werden kann.
Ein Plan wird vollständig durch die folgenden geometrischen Elemente bestimmt:
- Drei Punkte nicht ausgerichtet.
- Eine gerade Linie und ein Punkt außerhalb.
- Zwei parallele Linien oder zwei sich schneidende Linien.
Was den letzten Punkt betrifft, wissen Sie wahrscheinlich bereits, was es bedeutet, dass zwei Geraden parallel sind. Die Bedeutung von Sekantenlinien ist jedoch weniger bekannt. Wenn Sie also Fragen haben, können Sie hier nachlesen , was Sekantenlinien sind .
Wenn wir also eine der drei oben genannten Bedingungen haben, bedeutet das, dass wir einen Plan erstellen können.
Immobilien planen
Der Plan erfüllt folgende Merkmale:
- Eine Ebene enthält unendlich viele Punkte.
- Eine Ebene enthält unendlich viele Linien.
- Eine Ebene ist unbegrenzt, das heißt, sie ist eine Fläche, die sich grenzenlos im Raum erstreckt.
- Zwei sich schneidende Ebenen bestimmen eine Linie.
- Eine Linie, die einen Punkt in einer Ebene hat, ist dort nicht unbedingt enthalten. Damit eine Linie Teil einer Ebene ist, muss sie mindestens zwei Punkte in der Ebene haben.
- Unendliche Ebenen kreuzen eine Gerade.
- Eine Halbebene ist jeder der beiden Teile, in die eine Ebene geteilt wird, wenn sie durch eine ihrer Linien geschnitten wird.
Ebenengleichungen
In der analytischen Geometrie ist die Gleichung einer Ebene eine Gleichung, die es ermöglicht, jede Ebene mathematisch auszudrücken. Um die Gleichung einer Ebene zu finden, benötigen Sie also nur einen Punkt und zwei linear unabhängige Vektoren, die zu dieser Ebene gehören.

Wie wir jedoch oben bei der Erläuterung des Planbegriffs gesehen haben, gibt es mehrere Möglichkeiten, einen Plan zu bestimmen. Nun, genauso gibt es auch verschiedene Möglichkeiten, einen Plan analytisch auszudrücken.
Somit sind alle Arten von Gleichungen der Ebene: die Vektorgleichung , die parametrischen Gleichungen , die implizite (oder allgemeine) Gleichung und die kanonische (oder segmentale) Gleichung der Ebene.
Dann werden wir die Erklärung und Formel aller Gleichungen des Plans im Detail sehen.
Vektorgleichung der Ebene
Betrachten Sie einen Punkt und zwei Richtungsvektoren einer Ebene:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Die Formel für die Vektorgleichung einer Ebene lautet:
![]()
Oder gleichwertig:
![]()
Gold
![]()
Und
![]()
sind zwei Skalare, also zwei reelle Zahlen.
Parametrische Gleichungen der Ebene
Die Formel für die parametrische Gleichung einer Ebene lautet:
![]()
Gold:
-
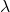
Und
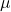
sind zwei Skalare, also zwei reelle Zahlen.
-
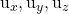
sind die Komponenten eines der beiden Leitvektoren des Plans
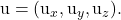
-
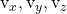
sind die Komponenten des anderen Richtungsvektors des Plans
Implizite oder allgemeine Gleichung der Ebene
Betrachten Sie einen Punkt und zwei Richtungsvektoren einer Ebene:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Die implizite, allgemeine oder kartesische Gleichung einer Ebene erhält man, indem man die folgende Determinante löst und das Ergebnis gleich 0 setzt:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Somit lautet die implizite oder allgemeine Gleichung des resultierenden Plans wie folgt:
![]()
Diese Art der Ebenengleichung wird auch als kartesische Ebenengleichung bezeichnet.
Kanonische oder segmentale Gleichung der Ebene
Die Formel für die kanonische oder segmentale Gleichung einer Ebene lautet wie folgt:
![]()
Gold:
-

ist der Schnittpunkt zwischen der Ebene und der X-Achse.
-

ist der Schnittpunkt zwischen der Ebene und der Y-Achse.
-

Hier schneidet die Ebene die Z-Achse.
Die kanonische Gleichung (oder Segmentgleichung) der Ebene kann auch aus ihrer allgemeinen Gleichung erhalten werden:
![]()
Zuerst lösen wir den Koeffizienten D aus der Gleichung:
![]()
Dann dividieren wir die gesamte Plangleichung durch den Wert des Parameters D mit geändertem Vorzeichen:
![]()
![]()
Und wenn wir die Eigenschaften von Brüchen nutzen, kommen wir zu folgendem Ausdruck:
![]()
Aus diesem Ausdruck leiten wir daher die Formeln ab, mit denen sich die Terme der kanonischen oder Segmentgleichung einer Ebene direkt berechnen lassen:
![]()
Um diese Variante der Plangleichungen bilden zu können, müssen daher die Koeffizienten A, B und C von Null verschieden sein, um so Unbestimmtheiten der Brüche zu vermeiden.
Relative Position zweier Ebenen
In der analytischen Geometrie gibt es nur drei mögliche relative Positionen zwischen zwei Ebenen: Schnittebenen, parallele Ebenen und zusammenfallende Ebenen.
- Sich schneidende Ebenen : Zwei Ebenen schneiden sich, wenn sie sich nur auf einer Linie schneiden.
- Parallele Ebenen : Zwei Ebenen sind parallel, wenn sie sich in keinem Punkt schneiden.
- Zusammenfallende Ebenen : Zwei Ebenen sind zusammenfallend, wenn sie alle gemeinsame Punkte haben.
sich schneidende Ebenen

parallele Ebenen

zusammenfallende Flugzeuge

Wenn sich außerdem zwei Schnittebenen in einem Winkel von 90° schneiden, handelt es sich um zwei zueinander senkrechte Ebenen .
Winkel zwischen zwei Ebenen
Der Winkel zwischen zwei Ebenen ist gleich dem Winkel, den die Normalenvektoren dieser Ebenen bilden. Um den Winkel zwischen zwei Ebenen zu ermitteln, wird daher der Winkel berechnet, den ihre Normalenvektoren bilden, da sie äquivalent sind.
Sobald wir also genau wissen, woraus der Winkel zwischen zwei Ebenen besteht, sehen wir uns die Formel zur Berechnung des Winkels zwischen zwei Ebenen im Raum an, die aus der Formel für den Winkel zwischen zwei Vektoren abgeleitet wird:
Gegeben sei die allgemeine (oder implizite) Gleichung zweier verschiedener Ebenen:
![]()
![]()
Der Normalenvektor jeder Ebene ist:
![]()
![]()
Und der von diesen beiden Ebenen gebildete Winkel wird bestimmt, indem der von ihren Normalenvektoren gebildete Winkel mit der folgenden Formel berechnet wird:
![]()
Nachdem wir den Kosinus des von den beiden Ebenen gebildeten Winkels anhand der Formel berechnet haben, müssen wir natürlich den Kosinus umkehren, um den Wert dieses Winkels zu ermitteln.
Wenn die beiden Ebenen hingegen senkrecht oder parallel sind, ist die Anwendung der Formel nicht erforderlich, da der Winkel zwischen den beiden Ebenen direkt bestimmt werden kann:
- Der Winkel zwischen zwei parallelen Ebenen beträgt 0°, da ihre Normalenvektoren die gleiche Richtung haben.
- Der Winkel zwischen zwei senkrechten Ebenen beträgt 90°, da ihre Normalenvektoren ebenfalls senkrecht (oder orthogonal) zueinander stehen und daher einen rechten Winkel bilden.