Hier erklären wir, was Änderungsrate, durchschnittliche Änderungsrate und momentane Änderungsrate sind. Sie können sich mehrere Beispiele zur Berechnung der Änderungsrate ansehen und zusätzlich mit gelösten Schritt-für-Schritt-Übungen zur Änderungsrate üben.
Wie hoch ist die Änderungsrate?
In der Mathematik ist die Änderungsrate (TV) einer Funktion die Differenz der Werte einer Funktion an zwei verschiedenen Punkten. Um die Änderungsrate zwischen zwei Punkten zu berechnen, müssen daher die Werte der Funktion an diesen beiden Punkten subtrahiert werden.
![]()
Wenn beispielsweise zwei Bilder einer Funktion f(2)=1 und f(5)=7 sind, beträgt ihre Änderungsrate:
![]()
Wir haben gerade die mathematische Bedeutung der Änderungsrate gesehen, aber in der Ökonomie bedeutet das Konzept der Änderungsrate Folgendes:
In der Ökonomie ist die Änderungsrate zwischen zwei Werten die prozentuale Differenz zwischen ihnen, d. h. die Änderungsrate einer Variablen zwischen verschiedenen Zeiträumen ist ihre relative Änderung. Um die Änderungsrate zu berechnen, werden daher die Werte der beiden unterschiedlichen Perioden subtrahiert und das erhaltene Ergebnis durch den Wert der Anfangsperiode dividiert.
![]()
Wenn beispielsweise der Wert bestimmter Aktien in einem Monat von 35 € auf 50 € gestiegen ist, beträgt die Änderungsrate:
![]()
In Anbetracht der beiden möglichen Bedeutungen der Änderungsrate konzentrieren wir uns in diesem Artikel auf das Verständnis der mathematischen Definition der Änderungsrate. Es können zwei Arten von Änderungsraten unterschieden werden: die durchschnittliche Änderungsrate und die momentane Änderungsrate. Unten finden Sie die Erklärung jedes Typs.
Durchschnittliche Änderungsrate
Die durchschnittliche Änderungsrate (TVM) einer Funktion in einem Intervall ist die Anzahl der Einheiten, um die die Funktion für jede Einheit zunimmt (oder abnimmt), um die ihre unabhängige Variable zunimmt. Daher wird die durchschnittliche Änderungsrate einer Funktion berechnet, indem das Wachstum der Funktion in einem Intervall durch die Amplitude dieses Intervalls dividiert wird.
![]()
Damit Sie sehen können, wie die durchschnittliche Änderungsrate berechnet wird, haben wir im Folgenden ein Beispiel Schritt für Schritt gelöst.
Beispiel für die Berechnung der durchschnittlichen Änderungsrate einer Funktion
- Berechnen Sie die durchschnittliche Änderungsrate im Intervall [2,5] der folgenden Funktion:
![]()
Zuerst berechnen wir den Wert der Funktion bei x=2 und x=5:
![]()
![]()
Und dann berechnen wir die durchschnittliche Änderungsrate der Funktion im Intervall, indem wir einfach die Formel anwenden:
![]()
![]()
Da das Ergebnis von TVM[2,5] positiv ist, bedeutet dies, dass die Funktion im Intervall [2,5] wächst. Wäre das Ergebnis hingegen negativ gewesen, würde dies bedeuten, dass die Funktion in diesem Intervall abnimmt.
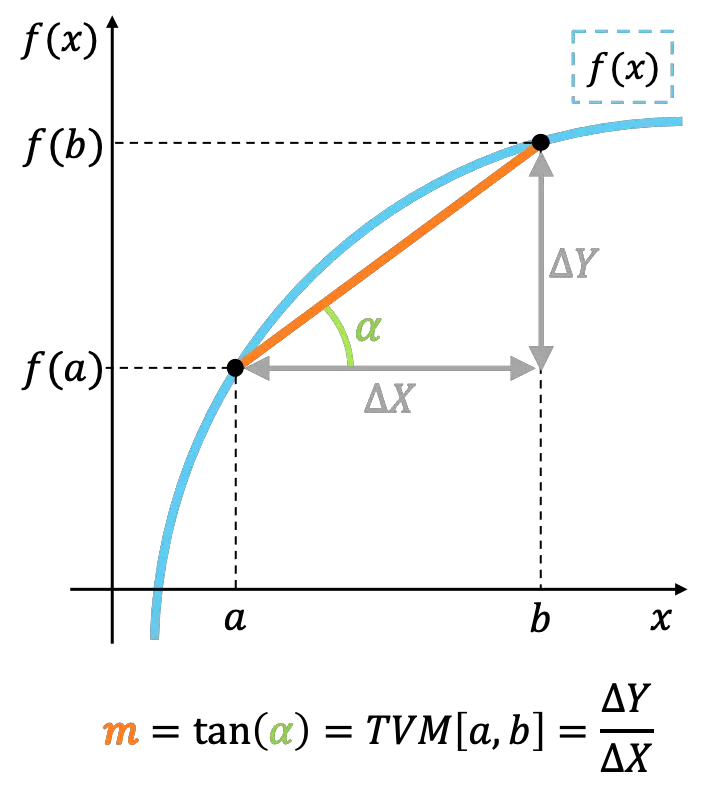
Geometrische Interpretation der durchschnittlichen Änderungsrate
Geometrisch gesehen stellt die durchschnittliche Änderungsrate einer Funktion in einem Intervall die Steigung der Linie dar, die die Extrempunkte des Intervalls verbindet.
Momentane Änderungsrate
Die momentane Änderungsrate (TVI) einer Funktion an einem Punkt ist die infinitesimale Grenze des relativen Anstiegs der Funktion über ein Intervall. Daher wird die momentane Änderungsrate berechnet, indem der Grenzwert des Quotienten von f(a+h)-f(a) gelöst wird, indem h gegen Null geht.
![]()
Der Wert der momentanen Änderungsrate kann positiv, negativ oder Null sein und bedeutet, dass die Funktion an diesem Punkt zunimmt, abnimmt oder gleich bleibt.
Beispiel für die Berechnung der momentanen Änderungsrate einer Funktion
- Berechnen Sie die momentane Änderungsrate am Punkt x=2 der folgenden Funktion:
![]()
Um die momentane Änderungsrate zu berechnen, müssen wir die Formel anwenden:
![]()
![]()
Wir lösen die bemerkenswerte Identität auf:
![]()
➤ Wenn Sie sich nicht mehr an die Formeln für bemerkenswerte Identitäten erinnern, finden Sie alle Formeln auf unserer auf Polynome spezialisierten Website: www.polinomios.org
Versuchen wir nun, das Limit zu lösen:
![]()
Wir finden jedoch keine Unbestimmtheit zwischen Null, daher:
![]()
➤ Siehe: So lösen Sie einen Grenzwert mit Nullunbestimmtheit zwischen Null
Und schließlich lösen wir das Limit:
![]()
Noch:
![]()
Da das Ergebnis von TVI(2) positiv ist, bedeutet dies, dass die Funktion bei x=2 zunimmt. Wäre das Ergebnis hingegen negativ gewesen, würde dies bedeuten, dass die Funktion in diesem Stadium abnimmt.
Geometrische Interpretation der momentanen Änderungsrate
Geometrisch gesehen stellt die momentane Änderungsrate einer Funktion an einem Punkt die Steigung der Tangente an die Funktion an diesem Punkt dar.
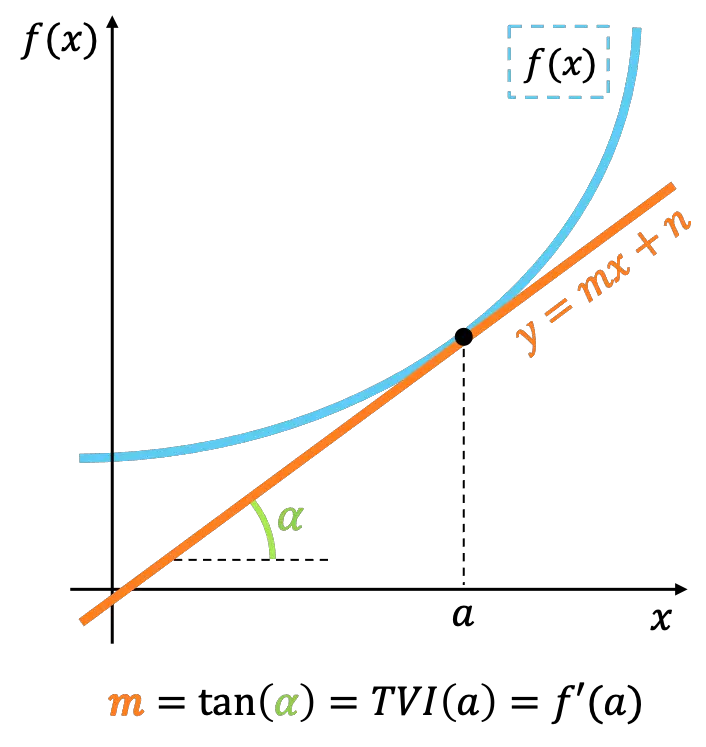
Wenn man genau hinschaut, entspricht die Bedeutung der momentanen Änderungsrate dem Konzept einer Ableitung einer Funktion . Daher wird die momentane Änderungsrate auch zur Berechnung des Wertes der Ableitung einer Funktion an einem Punkt verwendet.
Gelöste Übungen zur Änderungsrate
Übung 1
Berechnen Sie den Wert der Änderungsrate der folgenden Funktion im Intervall [1,3].
![]()
Zuerst bestimmen wir den Wert der Funktion an den Enden des Intervalls:
![]()
![]()
Und jetzt wenden wir die Formel für die Änderungsrate an:
![]()
![]()
Übung 2
Berechnen Sie die durchschnittliche Änderungsrate (TVM) der folgenden Funktion über das Intervall [1,4]:
![]()
Wir berechnen zunächst die Bilder der Funktion bei x=1 und x=4.
![]()
![]()
Und wir wenden die Formel für die durchschnittliche Änderungsrate an:
![]()
![]()
Übung 3
Ermitteln Sie die durchschnittliche Änderungsrate der folgenden Funktion im Intervall [-1,3]:
![]()
Um die durchschnittliche Änderungsrate zu bestimmen, müssen wir zunächst f(-1) und f(3) berechnen:
![]()
![]()
Wir verwenden nun die Formel für die durchschnittliche Änderungsrate:
![]()
![]()
Übung 4
Berechnen Sie die durchschnittliche Änderungsrate im Intervall [2,4] der in der folgenden Grafik gezeigten Funktion:

Wir wenden die Formel für die durchschnittliche Änderungsrate an:
![]()
![]()
Wie wir in der Formel sehen, müssen wir den Wert von f(4) und f(2) ermitteln. Und das lässt sich ganz einfach anhand der grafischen Darstellung der Funktion bewerkstelligen:
![]()
![]()
Und da wir nun die Werte der Funktion kennen, setzen wir sie in die Formel ein:
![]()
Übung 5
Berechnen Sie die momentane Änderungsrate der folgenden Funktion am Punkt x=2:
![]()
Um die momentane Änderungsrate der Funktion am Punkt x=2 zu bestimmen, wenden wir die entsprechende Formel an:
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73ee822823f921f75014cb9b50e47f51_l3.png)
Übung 6
Bestimmen Sie die momentane Änderungsrate (TVI) der folgenden Funktion am Punkt x=1:
![]()
Wir wenden die Formel für die momentane Änderungsrate an:
![]()
![]()
Dann berechnen wir
![]()
Und
![]()
![]()
![]()
Und wir ersetzen die im Grenzwert gefundenen Werte:
![]()
Wir lösen das bemerkenswerte Produkt:
![]()
Versuchen wir nun, das Limit zu lösen:
![]()
Aber wir finden die unbestimmte Form Null dividiert durch Null, also faktorisieren wir das Polynom des Zählers des Bruchs und vereinfachen:
![]()
➤ Wenn Sie nicht wissen , wie Sie die Nullunbestimmtheit zwischen Null lösen können , finden Sie im obigen Link die vollständige Erklärung zum Lösen eines Grenzwerts mit Nullunbestimmtheit zwischen Null.
Und schließlich lösen wir das Limit auf:
![]()
Zusammenfassend ist die momentane Änderungsrate der Funktion am Punkt x=1 gleich 2.
![]()
Übung 7
Ermitteln Sie die momentane Änderungsrate der folgenden Funktion am Punkt x=2:
![]()
Wir verwenden zunächst die Formel für die momentane Änderungsrate:
![]()
![]()
Wir berechnen
![]()
Und
![]()
![]()
![]()
Und wir ersetzen die im Grenzwert gefundenen Werte:
![Rendered by QuickLaTeX.com \text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ad59f5f751af139656a471bf2a41801_l3.png)
Wir berechnen die bemerkenswerte Gleichheit:
![]()
Wir operieren mit dem Zähler:
![]()
Versuchen wir nun, das Limit zu lösen:
![]()
Aber wir erhalten die Unbestimmtheit Null dividiert durch Null, also faktorisieren wir die Polynome und vereinfachen:
![]()
Und schließlich lösen wir das Limit auf:
![]()
Noch:
![]()