Polynomdivision

Auf dieser Seite erfahren Sie, wie man Polynome dividiert, sowohl die Division eines Polynoms durch ein Monom als auch die Division eines Polynoms durch ein anderes Polynom. Sie können sich auch Beispiele für die Division von Polynomen ansehen und mit Schritt-für-Schritt-Lösungen üben. Darüber hinaus finden Sie die Eigenschaften dieser Polynomoperation.

Polynomiale (oder polynomische) Division

Bevor wir genau sehen, wie zwei Polynome dividiert werden, werfen wir einen kurzen Blick auf die Konzepte der Polynomdivision, damit wir die Methode, die wir verwenden werden, leichter verstehen.

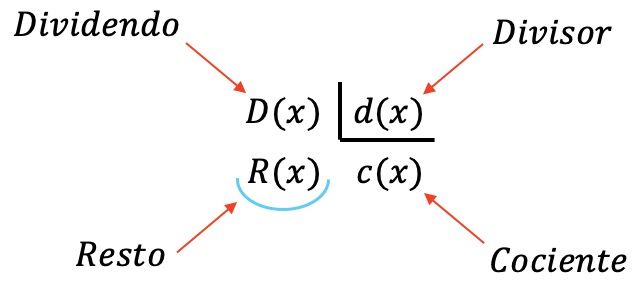
An einer Polynomdivision sind vier Polynome beteiligt:

• Dividende : das geteilte Polynom.
• Divisor : das Polynom, das den Dividenden teilt.
• Quotient : Ergebnis der Division der Dividende durch den Divisor.
• Rest (oder Residuum): das verbleibende Polynom bei der Division zwischen den beiden Polynomen.

Andererseits sollten Sie auch wissen, dass es zwei Arten der Division zwischen Polynomen gibt:

• Exakte Division von Polynomen : Eine Division zwischen Polynomen ist genau, wenn der Rest Null ist. In diesem Fall ist der Polynomdividende gleich dem Divisor multipliziert mit dem Quotienten.

Außerdem in diesem Fall die Dividende

ist ein Vielfaches des Divisors

und der Quotient

Ebenso sind sowohl der Polynomteiler als auch der Polynomquotient Teiler des Dividenden.

• Ganzzahlige Division von Polynomen : Bei einer ganzzahligen (oder ungenauen) Division von Polynomen ist der Rest ungleich Null (0). Dann ist die grundlegende Eigenschaft der Polynomdivision erfüllt:

Nachdem wir nun gesehen haben, was das Teilen von Polynomen ist, wollen wir uns nun ansehen, wie man Polynome durcheinander dividiert. Genauer gesagt erklären wir zunächst die Division zwischen einem Polynom und einem Monom und dann die Division zwischen zwei Polynomen.

Division eines Polynoms durch ein Monom

Bevor wir sehen, wie man ein Polynom durch ein Monom dividiert, erinnern wir uns zunächst daran, wie Monome zwischen ihnen geteilt werden, da man es wissen muss, um diese Art von Polynomoperation durchführen zu können.

Bei der Division zweier Monome werden ihre Koeffizienten durcheinander und ihre Literalteile durcheinander dividiert, d. h. die Koeffizienten der Monome werden dividiert und die Exponenten von Variablen mit derselben Basis werden subtrahiert. Schauen Sie sich das folgende Beispiel an:

Sehen wir uns nun an, was die Division eines Polynoms durch ein Monom beinhaltet:

Um in der Mathematik die Division eines Polynoms durch ein Monom zu lösen, wird jeder Term des Polynoms durch das Monom dividiert.

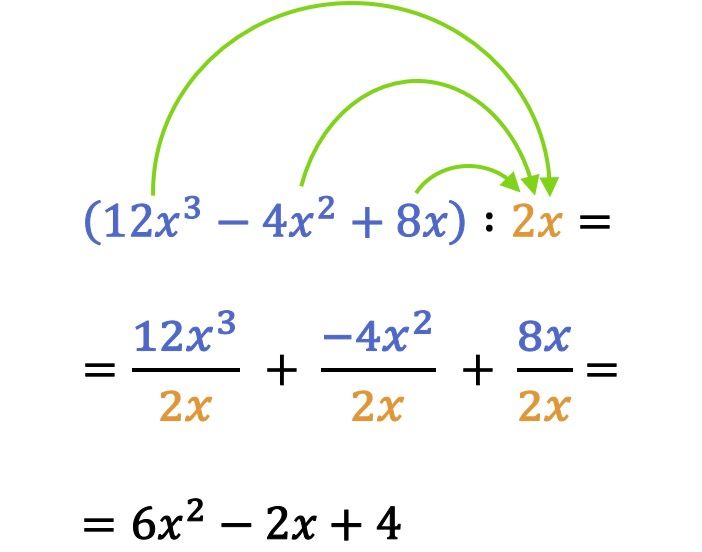
Beachten Sie im vorherigen Divisionsbeispiel, dass Sie bei der Division von Monomen oder Polynomen auch die Vorzeichenregel berücksichtigen müssen. Tatsächlich besteht ein sehr häufiger Fehler bei Divisionen zwischen Polynomen und Monomen darin, das Vorzeichen eines Termes falsch zu verstehen.

Division eines Polynoms durch ein anderes Polynom

Um zwei Polynome zu dividieren, müssen Sie einem Verfahren folgen. Sehen wir uns also an, wie die Methode zur Division von Polynomen, auch lange Division von Polynomen genannt, aussieht, indem wir Schritt für Schritt ein Beispiel lösen:

• Berechnen Sie das Ergebnis der Division des Polynoms

  

  zwischen dem Polynom

  

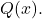
  Da es sich um zwei Polynome handelt:

Als Erstes müssen die Polynome in Divisionsform gebracht werden. Links schreiben wir den Zähler des Bruchs (Dividendenpolynom) und rechts den Nenner des Bruchs (Divisorpolynom):

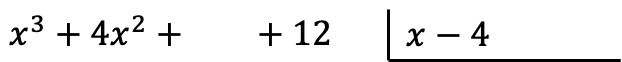
Warnung: Wenn ein Polynom kein Monom eines bestimmten Grades hat, müssen wir an seiner Stelle ein Leerzeichen lassen. Zum Beispiel das Polynom

Es gibt kein erstes Semester, daher gibt es stattdessen ein Leerzeichen.

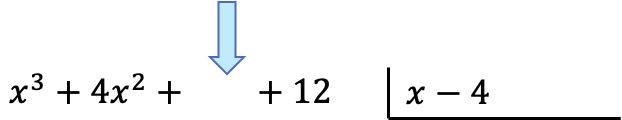
Sobald wir die Polynome erstellt haben, werden wir den Quotienten ermitteln. Und um den ersten Term des Quotienten zu finden, müssen wir den ersten Term des Dividenden durch den ersten Term des Divisors dividieren:

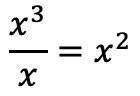
Und anstelle des Quotienten setzen wir das Ergebnis der Division:

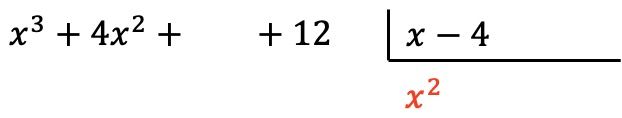
Jetzt multiplizieren wir den gefundenen Term mit jedem Element des Divisors und tragen jedes Ergebnis unter dem Dividenden in die entsprechende Spalte ein , wobei wir das Vorzeichen ändern :

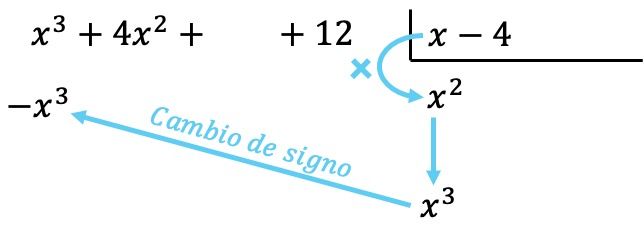
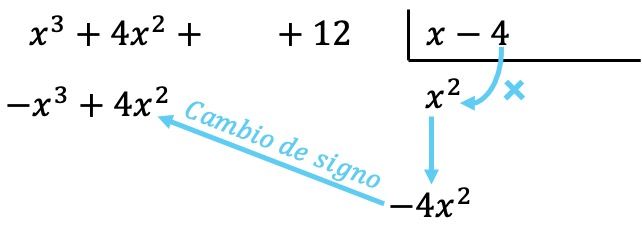
Wie bei allen Operationen mit Polynomen ist es wichtig, die Polynome vom höchsten zum niedrigsten Grad zu ordnen, sodass alle Terme desselben Grades in derselben Spalte stehen.

Nachdem wir die Multiplikationsergebnisse mit dem umgekehrten Vorzeichen platziert haben, müssen wir die vertikal ausgerichteten Terme hinzufügen:

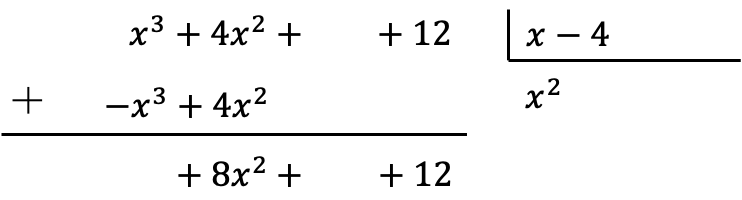
Beachten Sie, dass bei dieser Summe der Koeffizient mit dem höchsten Grad aufgehoben wird und wir daher einen Term weniger im Dividenden haben.

Wir müssen nun den gleichen Vorgang wiederholen, bis der Polynomdividende einen Grad kleiner ist als der Polynomteiler.

Wir dividieren daher den ersten Term des Dividenden durch den ersten Term des Divisors:

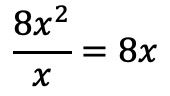
Das Ergebnis setzen wir in den Quotienten:

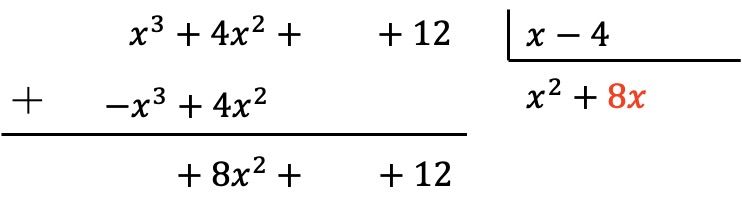
Wie zuvor multiplizieren wir den neuen Term des Quotienten mit jedem Element des Divisors und tragen die Ergebnisse mit entgegengesetztem Vorzeichen in die entsprechenden Spalten des Dividenden ein:

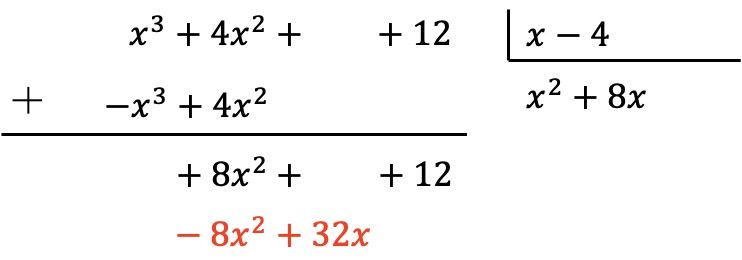
Und wir fügen vertikal hinzu:

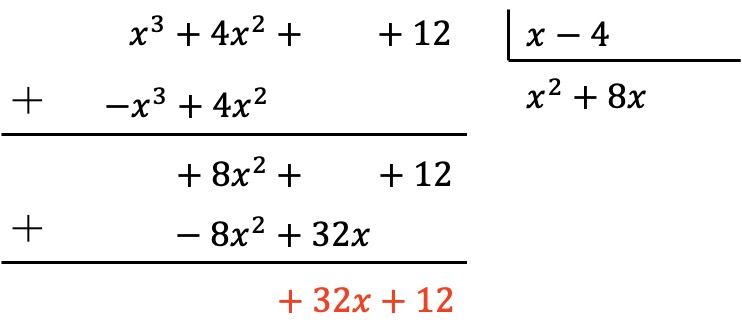
Das Dividendenpolynom ist immer noch nicht einen Grad kleiner als das Divisorpolynom, daher müssen wir mit dem gleichen Prozess fortfahren.

Zuerst dividieren wir also den ersten Term des Dividenden durch den ersten Term des Divisors, dann multiplizieren wir das Ergebnis mit jedem Term des Divisors, dann tragen wir die geänderten Ergebnisse mit Vorzeichen in den Dividenden ein und schließlich addieren wir vertikal:

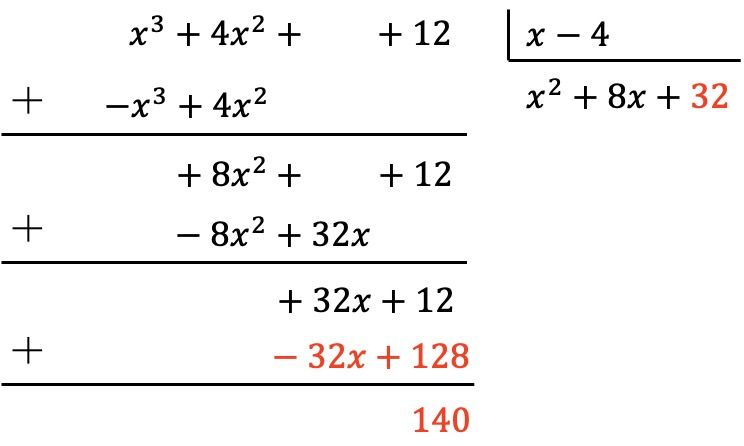
Wir haben also bereits festgestellt, dass das Polynom des Dividenden einen Grad kleiner als der Grad des Divisors hat, da der Dividend den Grad 0 und der Divisor den Grad 1 hat. Daher ist die Division vollständig.

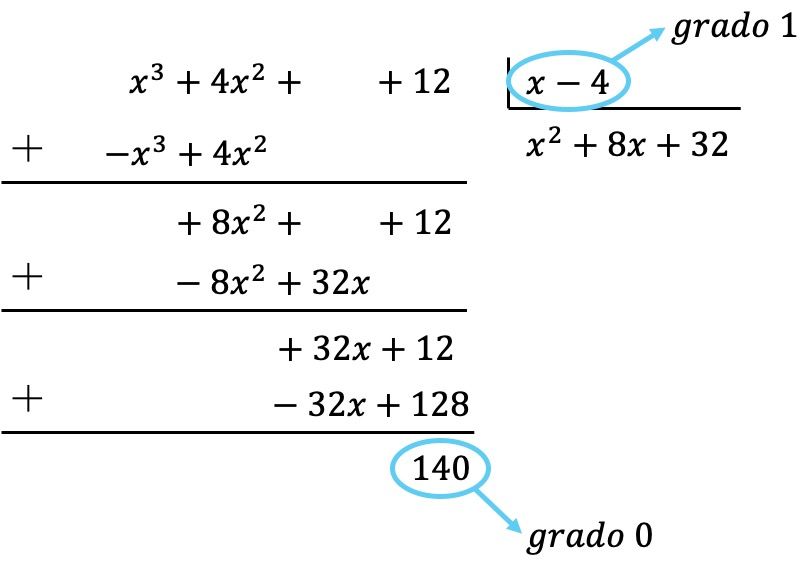
Das Ergebnis der Division ist also:

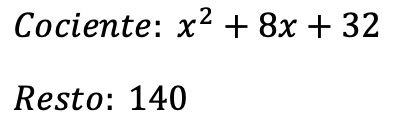
Andererseits können wir anhand der Grundbedingung für die Division von Polynomen überprüfen, ob wir die Polynomdivision korrekt durchgeführt haben:

✅

Die Gleichung ist erfüllt, die Polynomdivision wurde also korrekt durchgeführt.

Damit wir mit der Division von Polynomen fertig sind, hoffen wir, dass wir Ihnen mit dieser Erklärung weiterhelfen konnten. Was halten Sie von der Methode zur Division von Polynomen? Haben Sie Zweifel? Gefällt es dir? Oder wäre es Ihnen lieber, wenn es keine Polynomdivisionen gäbe? 😂 Wir haben dich in den Kommentaren gelesen! 👇👇👇

Eigenschaften dividierender Polynome

Jede Division von Polynomen erfüllt die folgenden Eigenschaften:

✓ Der Grad des Polynomdividenden muss immer größer sein als der Grad des Polynomdivisors.

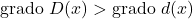✓ Der Grad des Polynomdividenden entspricht der Summe der Grade des Divisors und des Quotienten.

✓ Der Grad des Restes ist immer kleiner als der Grad des Divisors (und damit auch des Dividenden).

✓ Der Dividend ist gleich dem Produkt aus Divisor mal Quotient plus Rest. Diese Bedingung wird auch bei der Division von Zahlen gestellt.

Aufgaben zur Division von Polynomen gelöst

Übung 1

Bestimmen Sie das Ergebnis der folgenden Division eines Polynoms durch ein Monom:

Um ein Polynom durch ein Monom zu dividieren, müssen Sie die Division jedes Termes des Polynoms durch dieses Monom lösen:

Denken Sie daran, dass bei der Division zwischen Monomen die Koeffizienten untereinander dividiert werden und die Exponenten von Potenzen mit gleicher Basis subtrahiert werden.

Übung 2

Berechnen Sie die folgende Division eines Polynoms durch ein Monom:

Um ein Polynom durch ein Monom zu dividieren, müssen Sie jeden Term des Polynoms durch das besagte Monom dividieren:

Denken Sie daran, dass bei der Monomialdivision die Koeffizienten untereinander dividiert und die Exponenten von Potenzen mit gleicher Basis subtrahiert werden.

Übung 3

Lösen Sie die folgende Division eines Polynoms durch ein Monom:

Um ein Polynom durch ein Monom zu dividieren, müssen Sie die Division jedes Termes des Polynoms durch dieses Monom lösen:

Bedenken Sie, dass das dividierende Monom negativ ist und sich daher die Vorzeichen aller Divisionen ändern.

Übung 4

Führen Sie die folgende Division der Polynome durch:

Um Polynome zu dividieren, müssen Sie die oben erläuterte Methode anwenden:

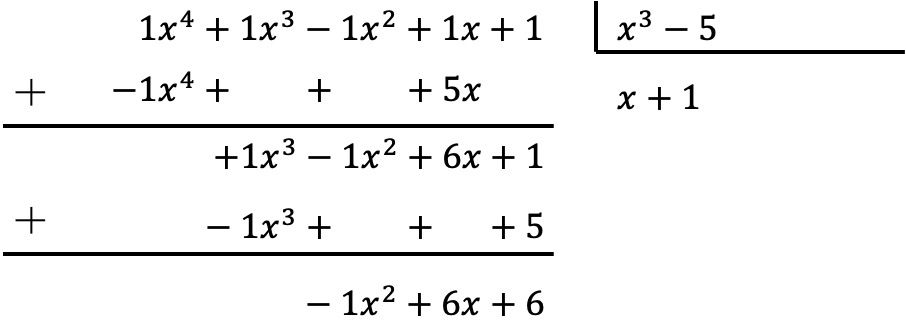
Das Ergebnis der Division zwischen den beiden Polynomen ist daher:

Quotient:

Ausruhen:

Übung 5

Berechnen Sie die folgende Division von Polynomen:

Um die Division des Polynoms durch das Binomial zu lösen, müssen wir die oben gesehene Methode anwenden:

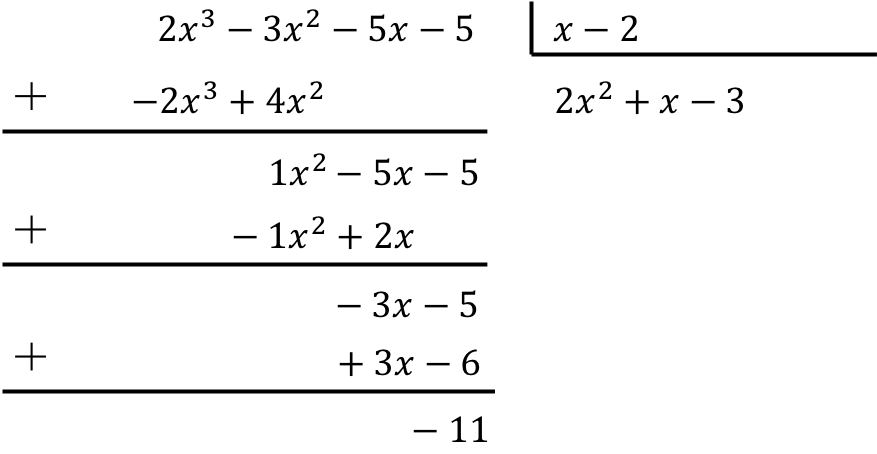
Das Ergebnis der Polynomdivision ist daher:

Quotient:

Ausruhen:

Übung 6

Lösen Sie die folgende Division von Polynomen:

Um die Division von Polynomen zu berechnen, müssen wir die erläuterte Methode anwenden:

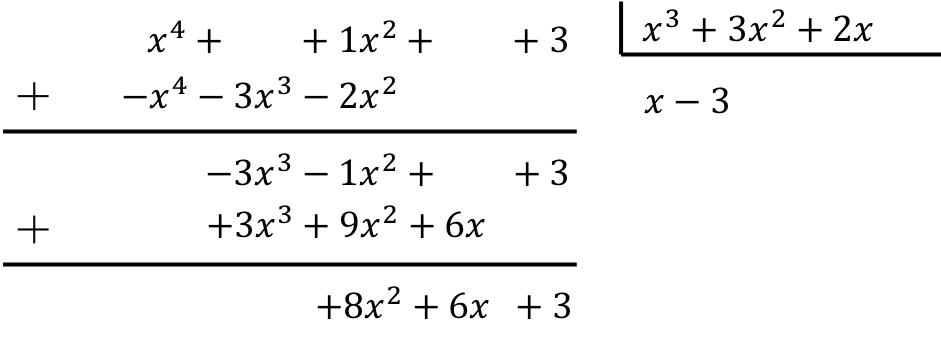
Das Ergebnis der Division zwischen den beiden Polynomen ist daher:

Quotient:

Ausruhen:

Übung 7

Finden Sie das Ergebnis der folgenden Division zwischen zwei Polynomen:

Um die Division des Polynoms durch das Trinom zu berechnen, müssen Sie die erläuterte Methode anwenden:

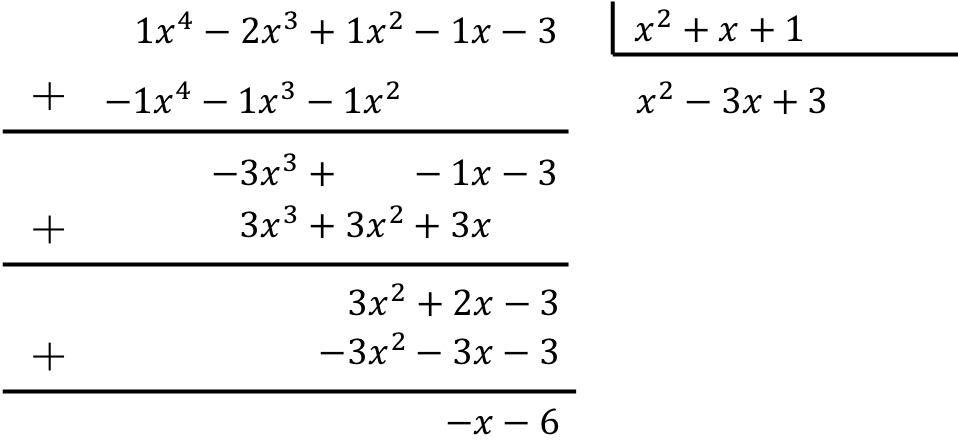
Das Ergebnis der Division zwischen den beiden Polynomen ist daher:

Quotient:

Ausruhen:

👉👉👉Wenn Sie es bis hierher geschafft haben, wissen Sie bereits, wie Polynome geteilt werden. Hell! Nachdem Sie nun die Division von Polynomen beherrschen, wissen Sie, dass es eine Methode gibt, mit der Sie bestimmte Divisionen zwischen Polynomen viel schneller lösen können . Dies ist eine synthetische Division oder Ruffini-Regel . Sie können sehen, wie dieser Trick angewendet wird und wann er verwendet werden kann, indem Sie auf den Link klicken.😉