Auf dieser Seite wird erklärt, was Funktionstransformationen sind und wie man sie findet. Es gibt drei Arten von Transformationen: Translationen (oder Verschiebungen), Symmetrien und Erweiterungen (oder Kontraktionen). Außerdem finden Sie Schritt für Schritt gelöste Übungen, damit Sie die Konzepte üben und verstehen können, ohne Zweifel zu hinterlassen.
Was sind Funktionstransformationen?
Manchmal werden wir gebeten, Elementarfunktionen grafisch darzustellen, die anderen, die wir bereits kennen, sehr ähnlich sind. Anstatt die ähnliche Funktion erneut darzustellen, können Techniken verwendet werden, um einfach und schnell von der Darstellung einer Funktion zu einer anderen zu wechseln.
Funktionstransformationen sind also Techniken, die es ermöglichen, durch elementare Operationen von der grafischen Darstellung einer Funktion zur grafischen Darstellung einer anderen, sehr ähnlichen Funktion zu gelangen.
Grundsätzlich gibt es drei Arten von Transformationen elementarer Funktionen:
- Übersetzungen oder Bewegungen : Eine Funktion kann vertikal und horizontal verschoben werden.
- Spiegelungen oder Symmetrien : Eine Funktion kann mithilfe der X-Achse oder der Y-Achse als Symmetrieachse gespiegelt werden.
- Erweiterungen und Komprimierungen : Eine Funktion kann vergrößert oder verkleinert werden.
Sobald wir das Konzept der Transformation einer Funktion kennengelernt haben, werden wir uns eingehender mit den einzelnen Modifikationsarten befassen.
Übersetzungen oder Bewegungen von Funktionen
Wir beginnen mit Funktionsverschiebungen. Es gibt zwei Arten: vertikale Übersetzungen und horizontale Übersetzungen.
Translation oder vertikale Bewegung einer Funktion
Um eine Funktion vertikal (entlang der Y-Achse) zu verschieben oder zu verschieben, müssen Sie der Funktion eine Konstante hinzufügen oder subtrahieren:
Wir verschieben eine Funktion um k Einheiten nach oben , indem wir ka zur Funktion hinzufügen:
Wir verschieben eine Funktion um k Einheiten nach unten , indem wir ka von der Funktion subtrahieren:
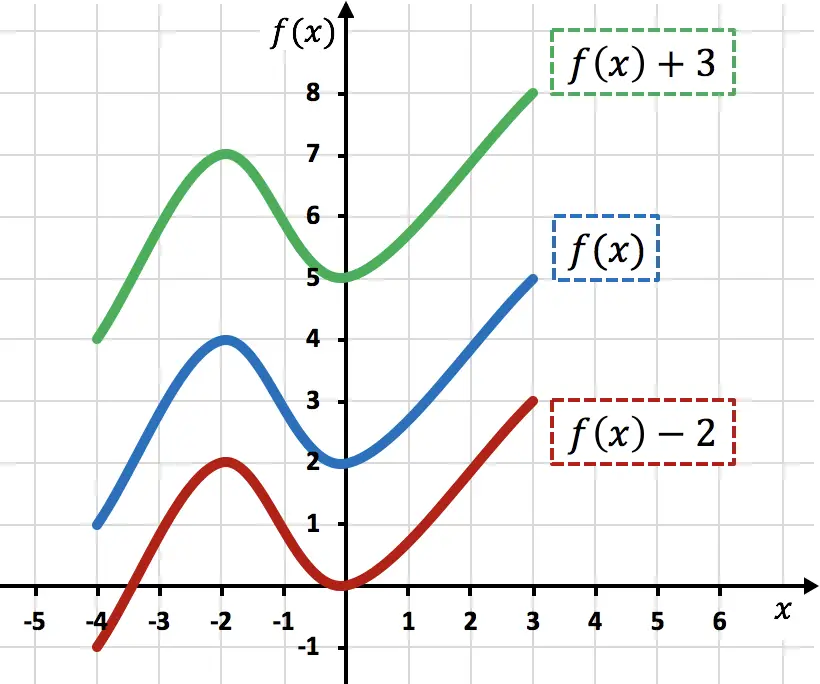
Wie Sie der Grafik entnehmen können, verschiebt das Hinzufügen einer Konstante zu einer Funktion die addierten Einheiten nach oben (grüne Funktion). Wenn man hingegen eine Zahl von einer Funktion subtrahiert, werden die subtrahierten Einheiten nach unten verschoben (rote Funktion).
Beachten Sie, dass bei dieser Art von Bewegungen nur die Y-Koordinaten der Funktionspunkte geändert werden, während die X-Koordinaten gleich bleiben.
Translation oder horizontale Bewegung von Funktionen
Um eine Funktion horizontal (entlang der X-Achse) zu verschieben oder zu verschieben, müssen Sie eine Konstante zur unabhängigen Variablen x addieren oder subtrahieren:
Die Grafik von
ist der Graph von
k Einheiten nach links verschoben.
Die Grafik von
ist der Graph von
k Einheiten nach rechts verschoben.
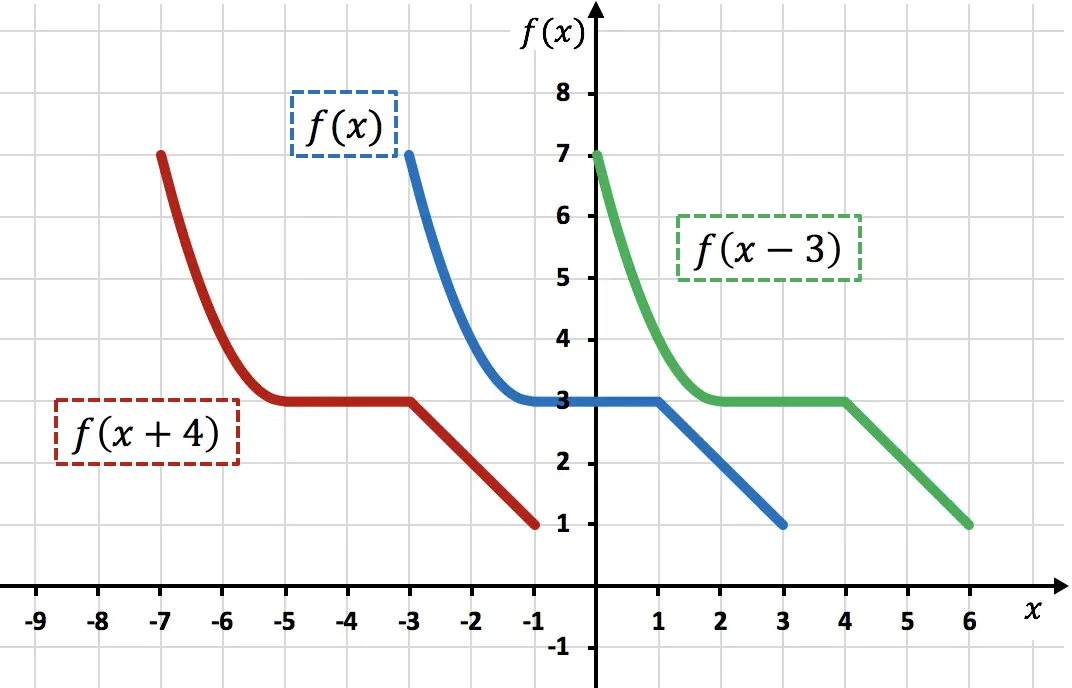
Wie Sie der Grafik entnehmen können, verschiebt die Funktion beim direkten Hinzufügen einer Konstante zur Variablen x die hinzugefügten Einheiten nach links (rote Funktion). Wenn andererseits eine Zahl von der Variablen x subtrahiert wird, verschiebt die Funktion die subtrahierten Einheiten nach rechts (grüne Funktion).
Beachten Sie, dass bei dieser Art von Bewegungen nur die X-Koordinaten der Funktionspunkte geändert werden, während die Y-Koordinaten weiterhin den gleichen Wert haben.
Beispiel für das Übersetzen oder Verschieben einer Funktion
- Verschieben Sie die folgende Funktion um 4 Einheiten nach oben und 3 Einheiten nach rechts:
Um die Funktion um 4 Einheiten nach oben zu verschieben, müssen wir der Funktion 4 Einheiten hinzufügen:
Und um die Funktion auch um 3 Einheiten nach rechts zu verschieben, müssen wir rechnen
. Daher, wo es eine gibt
wir können
Die um 4 Einheiten nach oben und 3 Einheiten nach rechts verschobene Funktion lautet daher:
Unten sehen Sie die ursprüngliche Funktion und die transformierte Funktion grafisch dargestellt, damit Sie den Unterschied zwischen ihnen sehen können:
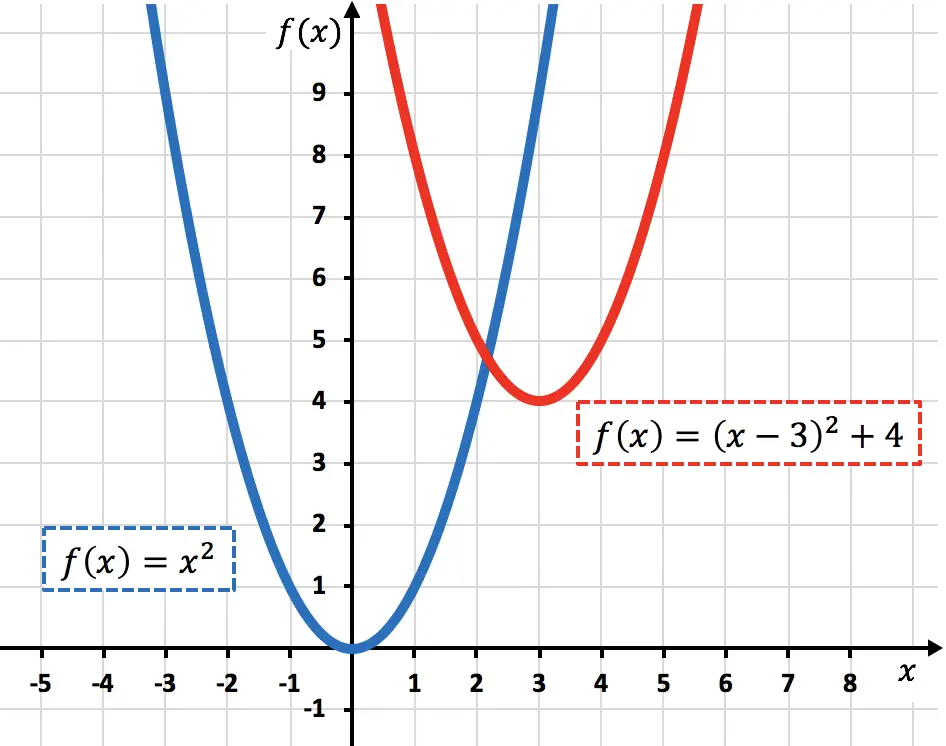
Manche Mathematiker sprechen von Schrägverschiebung oder Translation, wenn beide Bewegungsarten gleichzeitig auftreten.
Spiegelung oder Symmetrie einer Funktion bezüglich der Koordinatenachsen
Wir können die symmetrische Funktion in Bezug auf jede kartesische Achse folgendermaßen darstellen:
Um eine Funktion in Bezug auf die x-Achse darzustellen, müssen wir das Vorzeichen der Funktion ändern, das heißt, wir müssen berechnen
Um eine Funktion in Bezug auf die y-Achse darzustellen, müssen wir die unabhängige Variable x negieren, das heißt, wir müssen berechnen
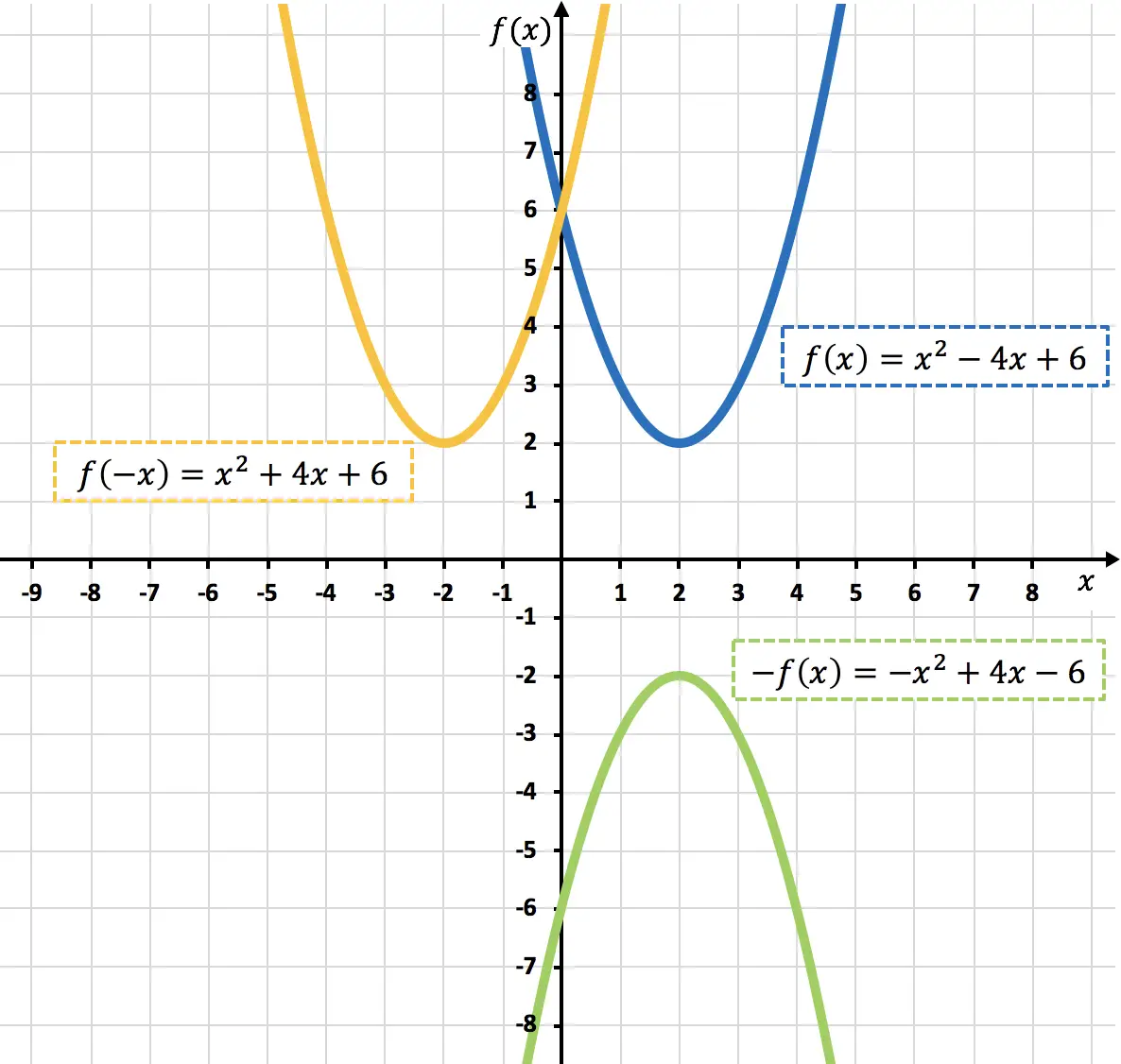
Wie Sie in der vorherigen Grafik sehen können, invertieren wir eine Funktion durch Multiplizieren mit -1 grafisch (orangefarbene Funktion), oder mit anderen Worten, wir spiegeln sie relativ zur X-Achse.
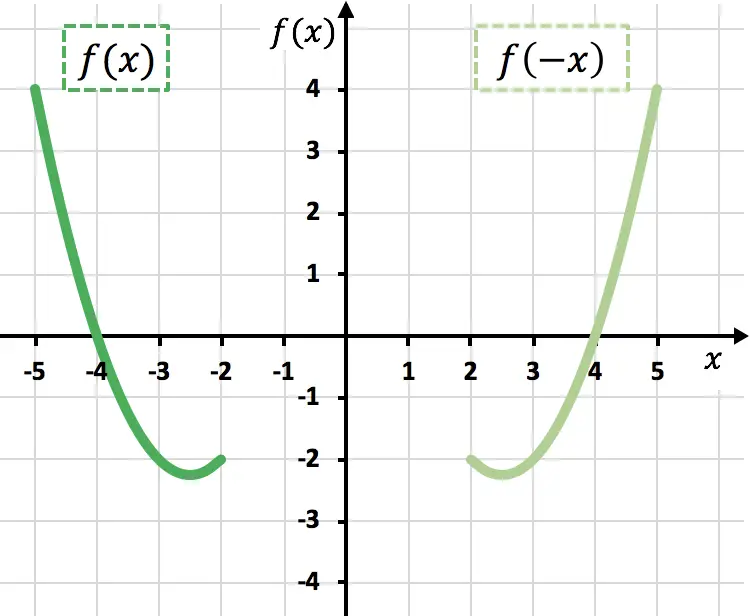
Wie im vorherigen Diagramm zu sehen ist, spiegeln wir durch Negation der Variablen x die Funktion in Bezug auf die Y-Achse (hellgrüne Funktion).
Beispiel für die Spiegelung einer Funktion
- Berechnen Sie die Symmetriefunktion um die OX-Achse und die Symmetriefunktion um die OY-Achse der folgenden quadratischen Funktion:
Um die Funktion symmetrisch in Bezug auf die X-Achse zu finden, müssen wir Folgendes tun
:
![-f(x)=-\bigl[x^2-4x+6\bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec1ca457c73589ee30ad6641f0d66c10_l3.png "Rendered by QuickLaTeX.com")
Und um die Funktion symmetrisch in Bezug auf die Y-Achse zu finden, müssen wir Folgendes tun
. Deshalb ersetzen wir dort, wo es eins gibt
in der ursprünglichen Funktion durch den Begriff
Nachfolgend haben Sie sowohl die ursprüngliche Funktion als auch die gefundenen symmetrischen Funktionen dargestellt:
Funktionserweiterungen und -kontraktionen
Wie bei Übersetzungen gibt es zwei Arten von Erweiterungen oder Kontraktionen: vertikale und horizontale.
Vertikale Erweiterung und Kontraktion einer Funktion
Indem wir eine ganzzahlige Funktion mit einem Koeffizienten multiplizieren, können wir sie erweitern oder verkleinern:
Um eine Funktion auf der Y-Achse zu erweitern (oder zu erweitern), müssen wir sie mit einer Zahl größer als 1 multiplizieren:
Um eine Funktion auf der Y-Achse zu reduzieren, müssen wir sie mit einer positiven Zahl kleiner als 1 multiplizieren:
Um eine Funktion auf der X-Achse zu reduzieren, müssen wir alle x mit einer Zahl größer als 1 multiplizieren:
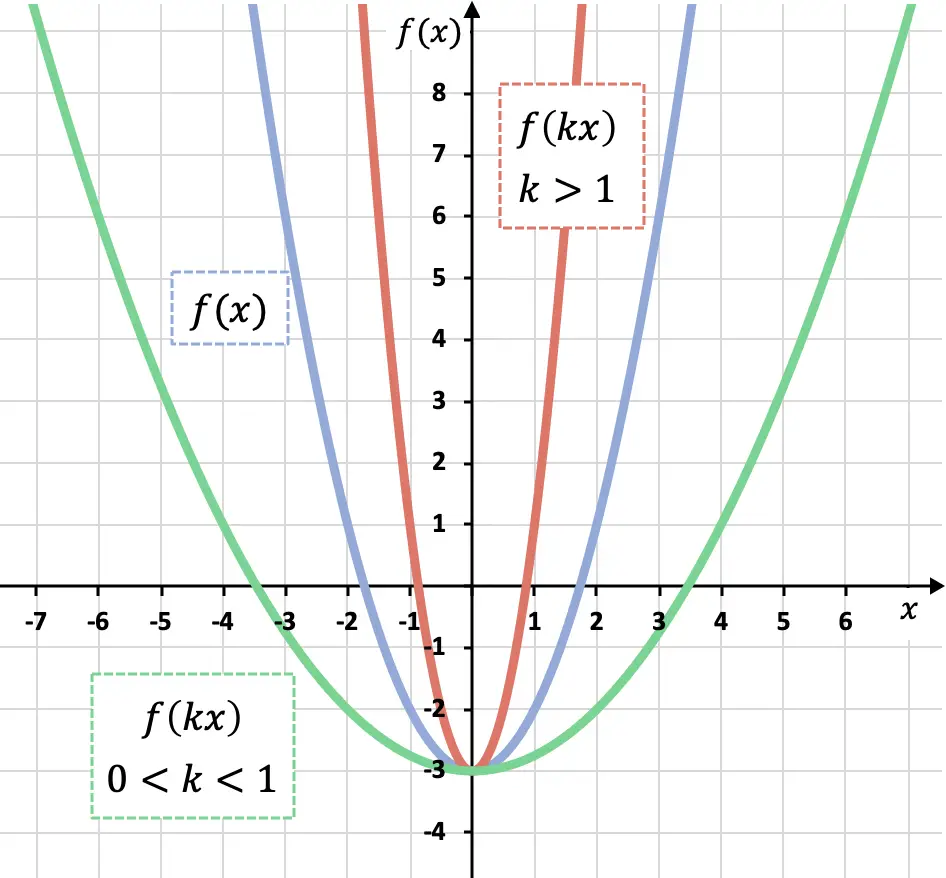
Wie Sie in der vorherigen Grafik sehen können, vergrößern wir sie entlang der OX-Achse, wenn wir alle x einer Funktion mit einem Koeffizienten größer als 0, aber kleiner als 1 multiplizieren (grüne Funktion). Wenn wir hingegen multiplizieren, vergrößern wir sie entlang der OX-Achse Wenn wir eine Funktion um einen Koeffizienten größer als 1 (rote Funktion) reduzieren, reduzieren wir sie entlang der OX-Achse.
Beispiel für das Erweitern oder Reduzieren einer Funktion
- Duplizieren Sie die folgende irrationale Funktion vertikal und horizontal:
Um die Funktion auf der y-Achse um zwei zu erweitern, müssen wir die gesamte Funktion mit 2 multiplizieren:
Und um die Funktion auch auf der x-Achse um zwei zu erweitern, müssen wir alle x der Funktion mit multiplizieren
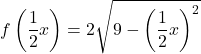
Die auf den beiden Koordinatenachsen duplizierte Funktion lautet daher:
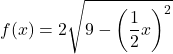
Unten sehen Sie die ursprüngliche Funktion und die transformierte Funktion grafisch dargestellt, damit Sie die Unterschiede zwischen ihnen sehen können:
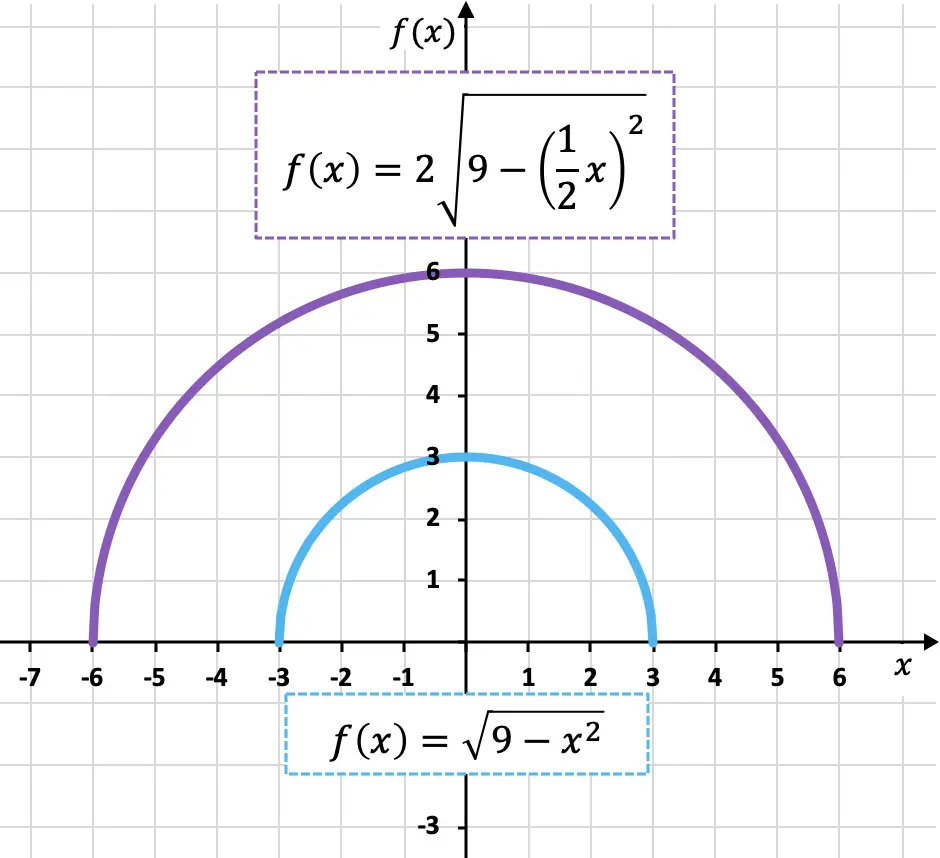
Wie Sie sehen können, ist das neue Feature (lila Farbe) sowohl vertikal als auch horizontal doppelt so groß wie das ursprüngliche Feature (blaue Farbe), daher wurde das Feature erweitert.
Übungen zu Funktionstransformationen gelöst
Übung 1
Verschieben Sie die folgende Funktion dritten Grades um 5 Einheiten nach oben:
Um die Funktion um 5 Einheiten nach oben zu verschieben, addieren Sie 5 zur Funktion:
![\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d29d1537293d975f7fbda8871622660f_l3.png "Rendered by QuickLaTeX.com")
Die um 5 Einheiten verschobene Funktion lautet also:
Übung 2
Finden Sie die symmetrische Funktion um die Y-Achse der folgenden quadratischen Funktion:
Um die Funktion symmetrisch zur Y-Achse zu finden, ist eine Berechnung erforderlich
, das heißt, wir müssen ersetzen
Für
in der Funktion:
Die symmetrische Funktion bezüglich der OY-Achse ist daher:
Übung 3
Führen Sie eine horizontale Komprimierung der folgenden Funktion auf ein Drittel ihrer Darstellung durch:
Um eine Funktion durch die zu reduzieren
Die reduzierte Funktion lautet daher:
Übung 4
Berechnen Sie die symmetrische Funktion in Bezug auf die OX-Achse der folgenden um 4 Einheiten nach rechts verschobenen Funktion:
Bevor wir die symmetrische Funktion berechnen, müssen wir die Funktion zunächst um 4 Einheiten nach rechts verschieben, also:
Und sobald wir die Funktion verschoben haben, berechnen wir die symmetrische Funktion bezüglich der X-Achse. Dazu müssen wir die erhaltene Funktion negieren:
![\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-62a7ea0e19503ec030dcdaa59c9157eb_l3.png "Rendered by QuickLaTeX.com")
Kurz gesagt lautet die Funktion nach Anwendung aller Elementaroperationen:
Übung 5
Verschieben Sie die folgende Funktion um 2 Einheiten nach links und erweitern Sie sie dann vertikal um den Faktor 4:
Zuerst verschieben wir die Funktion um zwei Einheiten nach links:
Und dann erweitern wir die Funktion entlang der Y-Achse mit dem Faktor 4:
![4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-07175c64db9d7e8074852df8944df6c4_l3.png "Rendered by QuickLaTeX.com")
Zusammenfassend lautet die Funktion nach Anwendung aller elementaren Transformationen:
Übung 6
Von der Funktion
Bestimmen Sie, welche der Darstellungen im Diagramm der Funktion entspricht
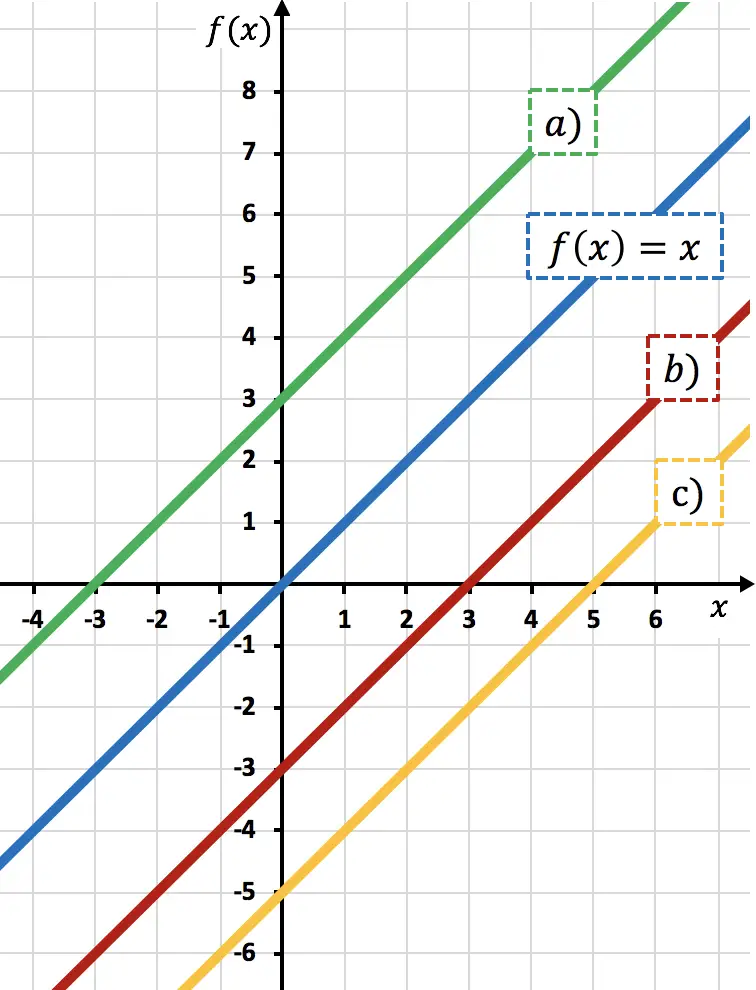
Funktion
ist die Funktion
3 Einheiten nach unten verschoben. Denn indem Sie eine Zahl von einer Funktion subtrahieren, verschieben Sie die Funktion nach unten.
Daher ist die Darstellung von
entspricht der Linie b) , da sie im Vergleich zu um 3 Einheiten nach unten verschoben ist
Dies lässt sich anhand der vertikalen Achse erkennen: wann
durch 0 geht, geht die rote Linie durch -3, also wird sie um 3 Einheiten nach unten verschoben.
Übung 7
Von der Funktion
Bestimmen Sie, welche Parabel die Darstellung der Funktion ist
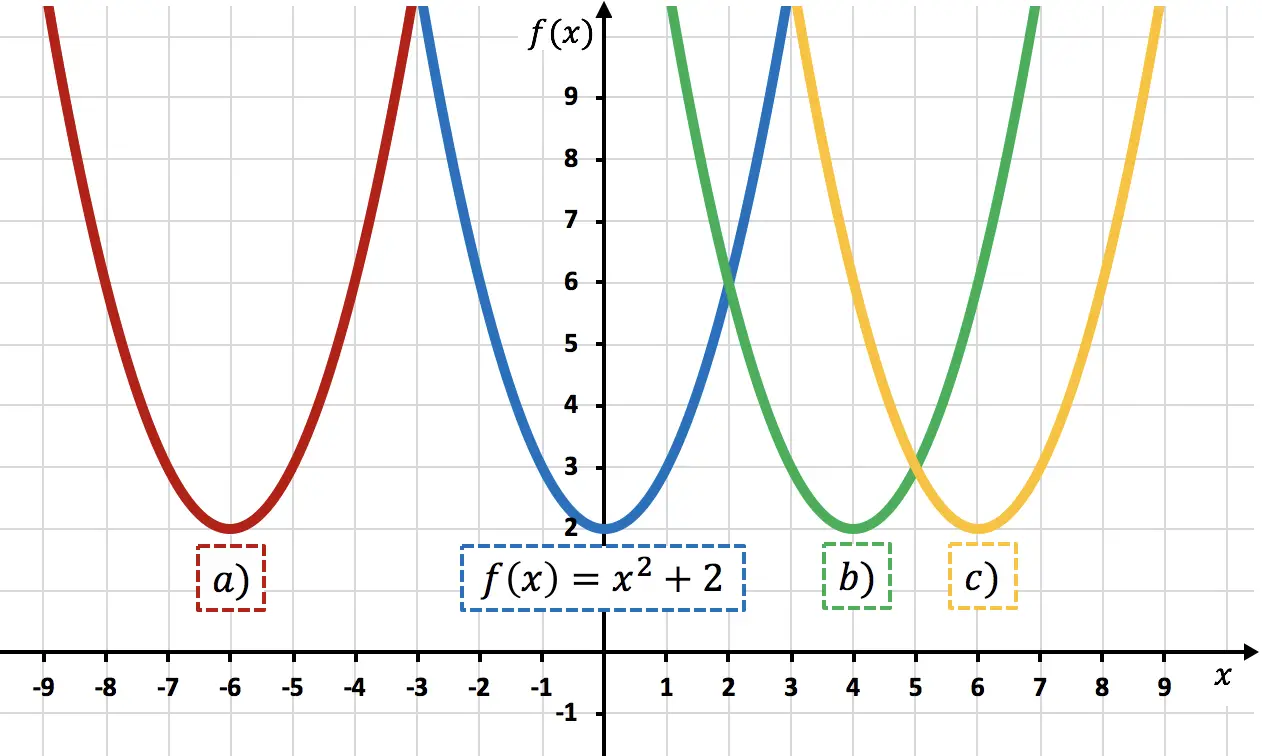
Funktion
ist die Funktion
6 Einheiten nach rechts verschoben. Wir können dies durch Berechnung überprüfen
Daher ist die Darstellung von
entspricht der Parabel c) , da sie im Vergleich zu um 6 Einheiten nach rechts verschoben ist
.
Dies kann man erkennen, wenn man sich die Scheitelpunkte der Parabeln anschaut: den Abstand zwischen den Scheitelpunkten der Parabel
und der Scheitelpunkt der Parabel c) beträgt 6 Einheiten, sodass letztere im Vergleich zur ersten um 6 Einheiten nach rechts verschoben ist.