In diesem Abschnitt erfahren Sie , wie Sie ein Gleichungssystem mit der Gauß-Jordan-Methode diskutieren und lösen . Das heißt, bestimmen Sie, ob es sich um ein determiniertes kompatibles System (DCS), ein unbestimmt kompatibles System (ICS) oder ein inkompatibles System handelt. Darüber hinaus finden Sie Beispiele und gelöste Übungen, damit Sie die Konzepte perfekt üben und verinnerlichen können.
Um zu verstehen, was wir als nächstes erklären werden, ist es wichtig, dass Sie bereits wissen, wie man ein System mit der Gauß-Methode löst. Wir empfehlen Ihnen daher, einen Blick darauf zu werfen, bevor Sie fortfahren.
Kompatible Systeme, bestimmt durch die Gauß-Methode
So lang wie die letzte Zeile der Gaußschen Matrix
![]()
, Sei
![]()
Und
![]()
Gibt es zwei beliebige Zahlen, ist dies ein SCD (System Compatible Determined). Daher verfügt das System über eine einzigartige Lösung .
Bei der überwiegenden Mehrheit der Systeme handelt es sich um SCD-Systeme.
Beispiel:
Wir haben zum Beispiel dieses System:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
Dessen erweiterte Matrix ist:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Um das System zu lösen, müssen wir die Zeilen der Matrix bearbeiten und alle Elemente unterhalb der Hauptdiagonale in 0 umwandeln. Also subtrahieren wir von der zweiten Zeile die erste Zeile und von der dritten Zeile subtrahieren wir die erste Zeile multipliziert mit 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Sobald alle Zahlen unterhalb der Hauptdiagonale 0 sind, kehren wir zurück, um das System in die Gleichungsform zu überführen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Dieses System ist also SCD , da die Matrix verschoben ist und die letzte Zeile vom Typ ist
![]()
. Deshalb lösen wir es wie immer: indem wir die Unbekannten von unten nach oben aus den Gleichungen eliminieren.
![]()
![]()
![]()
Da wir nun z kennen, setzen wir seinen Wert in die zweite Gleichung ein, um den Wert von zu ermitteln
![]()
:
![]()
![]()
![]()
![]()
![]()
Und schließlich machen wir dasselbe mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und lösen nach auf
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
Die Lösung des Gleichungssystems lautet daher:
![]()
Inkompatible Systeme nach der Gauß-Methode
In der Gauß-Matrix haben wir eine Zeile mit drei Nullen hintereinander und einer Zahl
![]()
, es ist ein IS (Inkompatibles System) und daher hat das System keine Lösung .
Beispiel:
Stellen Sie sich zum Beispiel vor, dass wir nach der Arbeit mit der Gaußschen Matrix eines Systems Folgendes übrig haben:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Wie die letzte Zeile ist
![]()
, also drei Nullen gefolgt von einer Zahl am Ende, ist ein IF (Inkompatibles System) und daher hat das System keine Lösung .
Obwohl es nicht notwendig ist, es zu wissen, werden Sie unten sehen, warum es keine Lösung gibt.
Wenn wir die letzte Zeile nehmen, hätten wir diese Gleichung:
![]()
Diese Gleichung wird niemals erfüllt werden, denn egal, welchen Wert z annimmt, eine Multiplikation mit 0 ergibt niemals 2 (jede Zahl, die mit 0 multipliziert wird, ergibt immer 0). Und da diese Gleichung niemals erfüllt sein wird, hat das System keine Lösung.
Kompatible Systeme, unbestimmt durch die Gaußsche Methode
Immer wenn eine Zeile der Gaußschen Matrix mit 0 gefüllt ist
![]()
Es handelt sich um ein SCI (Indeterminate Compatible System) und daher hat das System unendlich viele Lösungen .
Sehen wir uns ein Beispiel für die Lösung eines ICS an:
Beispiel:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Wie immer erstellen wir zunächst die erweiterte Matrix des Systems :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Jetzt wollen wir, dass alle Zahlen unterhalb der Hauptdiagonale 0 sind. Also addieren wir zur zweiten Zeile die erste Zeile multipliziert mit -2:
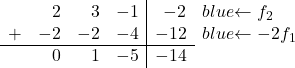
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
Um 3 in 0 umzuwandeln, addieren wir in der dritten Zeile die erste Zeile multipliziert mit -3:
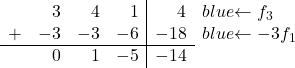
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Um die 1 in der letzten Zeile in 0 umzuwandeln, addieren wir in der dritten Zeile die zweite Zeile multipliziert mit -1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Da die letzte Zeile alle 0 ist , können wir sie entfernen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
Und da wir eine ganze Zeile mit Nullen gefüllt hatten, ist dies ein SCI.
Somit erhalten wir folgendes System:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Wenn es sich bei dem System um ein SCI handelt, muss der Wert des Parameters von einer Unbekannten übernommen werden
![]()
. Und wir müssen das System basierend auf diesem Parameter lösen
![]()
.
Daher weisen wir den Wert von zu
![]()
zu z :
![]()
Allerdings hätten wir auch jede andere Unbekannte wählen können, um den Wert zu ermitteln
![]()
.
Jetzt isolieren wir y aus der zweiten Gleichung und lassen es eine Funktion von sein
![]()
:
![]()
![]()
![]()
Und schließlich streichen wir x aus der ersten Gleichung und belassen es ebenfalls als Funktion von
![]()
:
![]()
![]()
![]()
![]()
Die Systemlösungen sind daher:
![]()
Wie Sie sehen können, hängen die Lösungen bei einem SCI-System vom Parameter ab
![]()
. Und denken Sie daran, dass es unendlich viele Lösungen gibt, denn je nachdem, welchen Wert es annimmt
![]()
, die Lösung wird die eine oder die andere sein.
Bevor wir mit den gelösten Übungen fortfahren, sollten Sie wissen, dass wir in diesem Artikel zwar die Gauß-Methode verwenden, eine andere Möglichkeit, lineare Gleichungssysteme zu diskutieren und zu lösen , der Satz von Rouche ist. Tatsächlich wird es wahrscheinlich häufiger verwendet.
Gelöste Aufgaben zur Diskussion von Gleichungssystemen nach der Gauß-Jordan-Methode
Übung 1
Bestimmen Sie, um welche Art von System es sich handelt, und lösen Sie das folgende Gleichungssystem mit der Gauß-Methode:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
Als erstes müssen wir die erweiterte Matrix des Systems erstellen:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Jetzt müssen wir alle Zahlen unterhalb des Hauptarrays auf 0 setzen.
Wir führen daher Zeilenoperationen durch, um die letzten beiden Terme der ersten Spalte zu löschen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
Wir haben eine Zeile der Matrix erhalten, die aus drei Nullen gefolgt von einer Zahl besteht. Es handelt sich also um ein IS (Inkompatibles System) und das System hat keine Lösung.
Übung 2
Bestimmen Sie, um welche Art von System es sich handelt, und finden Sie mithilfe der Gauß-Methode die Lösung für das folgende Gleichungssystem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
Als erstes müssen wir die erweiterte Matrix des Systems erstellen:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Jetzt müssen wir alle Zahlen unterhalb des Hauptarrays auf 0 setzen.
Wir führen daher Zeilenoperationen durch, um die letzten beiden Terme der ersten Spalte zu löschen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Versuchen wir nun, das letzte Element aus der zweiten Spalte zu entfernen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Aber wir bekommen eine ganze Reihe von Nullen. Das ist also ein SCI und das System hat unendlich viele Lösungen.
Aber da es sich um ein ICS handelt, können wir das System basierend darauf lösen
![]()
. Wir löschen daher die 0-Zeile:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
Wir drücken die Matrix nun in Form eines Gleichungssystems mit Unbekannten aus:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
Wir geben den Wert von an
![]()
Für
![]()
![]()
Wir ersetzen den Wert von
![]()
in der zweiten Gleichung, um den Wert von zu finden
![]()
![]()
![]()
![]()
Und das Gleiche machen wir mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und löschen sie
![]()
![]()
![]()
![]()
![]()
Die Lösung des Gleichungssystems lautet daher:
![]()
Übung 3
Finden Sie heraus, um welche Art von System es sich handelt, und lösen Sie das folgende Gleichungssystem mit der Gauß-Methode:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
Als erstes müssen wir die erweiterte Matrix des Systems erstellen:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Um die Gauß-Methode anzuwenden, ist es einfacher, wenn die erste Zahl in der ersten Zeile eine 1 ist. Wir werden daher die Reihenfolge der Zeilen 1 und 2 ändern:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Jetzt müssen wir alle Zahlen unterhalb des Hauptarrays auf 0 setzen.
Wir führen daher Zeilenoperationen durch, um die letzten beiden Terme der ersten Spalte zu löschen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Jetzt konvertieren wir das letzte Element der zweiten Spalte auf Null:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Dieses System ist SCD , da es uns gelungen ist, die Matrix zu verschieben und die letzte Zeile vom Typ ist
![]()
. Daher wird es eine einzigartige Lösung geben.
Sobald alle Zahlen unterhalb der Hauptdiagonale 0 sind, können wir nun das Gleichungssystem lösen. Dazu drücken wir die Matrix noch einmal in Form eines Gleichungssystems mit Unbekannten aus:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
Und wir lösen die Unbekannten der Gleichungen von unten nach oben. Wir lösen zunächst die letzte Gleichung:
![]()
![]()
Jetzt setzen wir den Wert von z in die zweite Gleichung ein, um den Wert von y zu ermitteln:
![]()
![]()
![]()
![]()
![]()
Und das Gleiche machen wir mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und lösen nach x auf:
![]()
![]()
![]()
![]()
Die Lösung des Gleichungssystems lautet daher:
![]()
Übung 4
Bestimmen Sie, um welche Art von System es sich handelt, und lösen Sie das folgende Gleichungssystem mit der Gauß-Methode:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
Als erstes müssen wir die erweiterte Matrix des Systems erstellen:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Jetzt müssen wir alle Zahlen unterhalb des Hauptarrays auf 0 setzen.
Wir führen daher Zeilenoperationen durch, um die letzten beiden Terme der ersten Spalte zu löschen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Versuchen wir nun, das letzte Element aus der zweiten Spalte zu entfernen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Aber wir bekommen eine ganze Reihe von Nullen. Das ist also ein SCI und das System hat unendlich viele Lösungen.
Aber da es sich um ein ICS handelt, können wir das System basierend darauf lösen
![]()
. Wir löschen daher die 0-Zeile:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
Wir drücken die Matrix nun in Form eines Gleichungssystems mit Unbekannten aus:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
Wir geben den Wert von an
![]()
Für
![]()
![]()
Wir ersetzen den Wert von
![]()
in der zweiten Gleichung, um den Wert von zu finden
![]()
![]()
![]()
![]()
![]()
Und das Gleiche machen wir mit der ersten Gleichung: Wir ersetzen die Werte der anderen Unbekannten und löschen sie
![]()
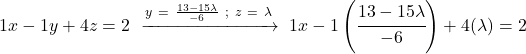
![]()
![]()
Wir haben eine Summe mit Brüchen. Daher bringen wir alle Begriffe auf einen gemeinsamen Nenner:
![]()
![]()
Da sie jetzt alle den gleichen Nenner haben, können wir sie zu einem einzigen Bruch zusammenfassen:
![]()
Und schließlich operieren wir mit dem Zähler:
![]()
![]()
Die Lösung des Gleichungssystems lautet daher:
![]()