In diesem Artikel erklären wir, was direkte Proportionalitätsfunktionen sind, wie ihre Formel lautet, wie man sie in einem Diagramm darstellt und wie man ihre Gleichung von einem bestimmten Punkt aus berechnet.
Was ist eine direkte Proportionalitätsfunktion?
Die direkte Proportionalitätsfunktion ist eine Funktion, die zwei direkt proportionale Größen in Beziehung setzt. Um den Wert der abhängigen Variablen (y) zu berechnen, muss daher der Wert der abhängigen Variablen (x) mit der Proportionalitätskonstante multipliziert werden.
Die direkte Proportionalitätsfunktion wird auch lineare Funktion genannt.
Denken Sie daran, dass zwei Größen direkt proportional sind, wenn der Wert einer Größe zunimmt, während die andere Größe ebenfalls zunimmt, und umgekehrt.
Formel für die direkte Proportionalitätsfunktion
Die Formel, die die direkte Proportionalitätsfunktion definiert, lautet wie folgt:
![]()
Dabei ist y die unabhängige Variable, x die abhängige Variable und ym die Steigung oder Proportionalitätskonstante der Funktion.
Wie Sie sehen, ist es mit dieser Formel sehr einfach, Werte der Größe y zu berechnen. Multiplizieren Sie einfach den Wert der Größe x mit der Steigung der Funktion, die für jede direkte Proportionalitätsfunktion charakteristisch ist.
Wenn wir zum Beispiel die folgende direkte Proportionalitätsfunktion haben:
![]()
Wenn wir bestimmen wollen, wie groß die Größe y ist, wenn x 5 ist, müssen wir nur die Steigung der Funktion (3) mit 5 multiplizieren:
![]()
Grafische Darstellung einer direkten Proportionalitätsfunktion
Als nächstes werden wir sehen, wie man direkte Proportionalitätsfunktionen grafisch darstellt. Als Beispiel machen wir folgende Übung:
![]()
Um die direkte Proportionalitätsfunktion in einem Diagramm darzustellen, zeichnen Sie einfach eine Linie, die durch den Koordinatenursprung (Punkt (0,0)) verläuft und die Steigung der Funktion aufweist.
In diesem Fall hat die Funktion, die wir darstellen möchten, eine Steigung von
![]()
Daher muss die Linie für jede Einheit von x um zwei Einheiten von y wachsen.
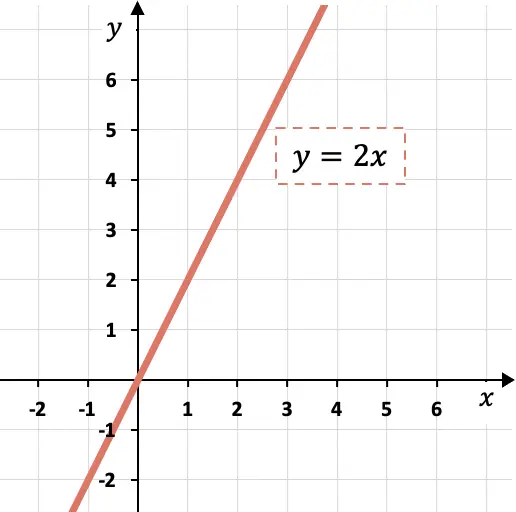
Wie Sie dem Diagramm entnehmen können, bedeutet eine Steigung von 2, dass die y-Größe doppelt so stark zunimmt wie die x-Größe.
Direkte Proportionalitätsfunktionen haben einen sehr ähnlichen Graphen wie affine Funktionen, es handelt sich jedoch um zwei verschiedene Arten von Funktionen. Die Unterschiede zwischen einer affinen Funktion und einer linearen Funktion können Sie im folgenden Link sehen:
➤ Siehe: Unterschied zwischen linearer und affiner Funktion
So finden Sie die direkte Proportionalitätsfunktion
Wenn wir einen Punkt der direkten Proportionalitätsfunktion kennen, können wir seine Gleichung leicht finden. Sehen wir uns an, wie dies durch Lösen eines direkten Proportionalitätsfunktionsproblems erreicht wird:
- Die Anzahl der Räume, die ein Maler streicht, ist ungefähr direkt proportional zu den Stunden, die er arbeitet, d. h. je mehr Stunden er arbeitet, desto mehr Räume kann er streichen. Wenn wir wissen, dass er an einem 8-Stunden-Tag zwei ganze Räume gestrichen hat, wie lautet dann die direkte Proportionalitätsfunktion, die die Anzahl der gestrichenen Räume mit den geleisteten Arbeitsstunden in Beziehung setzt?
Zuerst müssen wir bestimmen, welche die abhängige Variable und welche die unabhängige ist. Die Anzahl der bemalten Teile hängt von den geleisteten Arbeitsstunden ab und nicht umgekehrt. Daher ist die unabhängige Variable (x) die Anzahl der geleisteten Arbeitsstunden und die abhängige Variable (y) die Anzahl der gestrichenen Räume.
Das Problem sagt uns, dass der Maler zwei Räume in 8 Stunden streichen kann, daher muss der Graph der Funktion durch den Punkt (8,2) verlaufen.
![]()
Darüber hinaus weist die Aussage darauf hin, dass zwischen den beiden Größen eine direkte proportionale Beziehung besteht, was bedeutet, dass sie mathematisch mit der Formel der direkten Proportionalitätsfunktion zusammenhängen:
![]()
Wir können nun den Wert der Steigung der Funktion berechnen, indem wir die Koordinaten des Punktes (8,2) in die Gleichung einsetzen:
![]()
Und schließlich lösen wir die Unbekannte m der Gleichung:
![]()
![]()
![]()
Kurz gesagt ist die direkte Proportionalitätsfunktion des Problems:
![]()
Das könnte Ihnen auch gefallen: