Differenzierbarkeit einer funktion

September 17, 2023

In diesem Artikel erfahren Sie, wie Sie die Differenzierbarkeit einer Funktion untersuchen, also ob eine Funktion differenzierbar ist oder nicht. Darüber hinaus werden wir den Zusammenhang zwischen Differenzierbarkeit und Stetigkeit einer Funktion sehen. Und schließlich werden wir die Differenzierbarkeit einer stückweisen Funktion untersuchen.

Differenzierbarkeit und Stetigkeit einer Funktion

Die Stetigkeit und Differenzierbarkeit einer Funktion an einem Punkt hängen wie folgt zusammen:

Wenn eine Funktion an einem Punkt differenzierbar ist, ist die Funktion an diesem Punkt stetig.
Wenn eine Funktion an einem Punkt nicht stetig ist, ist sie an diesem Punkt auch nicht differenzierbar.

Die Umkehrung dieses Theorems ist jedoch falsch: Nur weil eine Funktion an einem Punkt stetig ist, heißt das nicht, dass sie an diesem Punkt immer differenzierbar ist.

Sie können auch anhand ihrer grafischen Darstellung erkennen, ob eine Funktion an einem Punkt differenzierbar ist oder nicht:

Handelt es sich um einen glatten Punkt, ist die Funktion an diesem Punkt differenzierbar.
Handelt es sich um einen Winkelpunkt, ist die Funktion an diesem Punkt stetig, aber nicht differenzierbar.

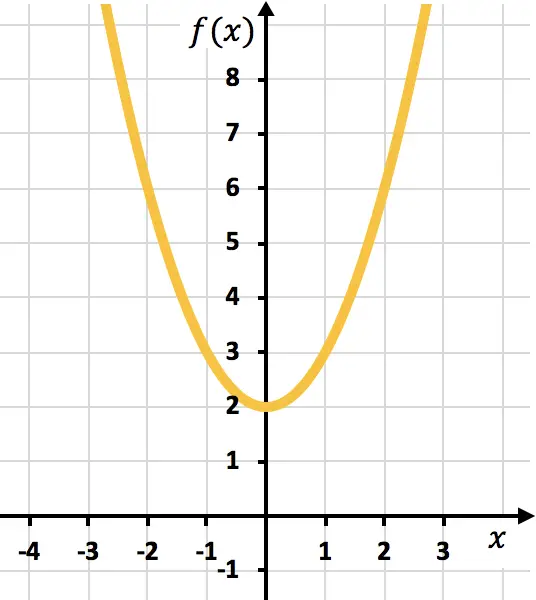
Glättungspunkt bei x=0:
kontinuierliche und differenzierbare Funktion in diesem Stadium.

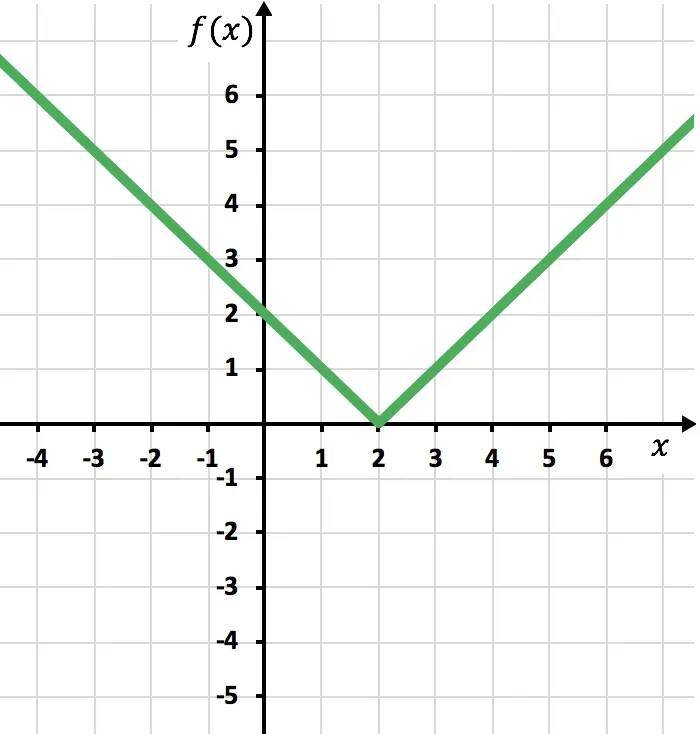
Winkelpunkt bei x=2:
Funktion stetig, aber zu diesem Zeitpunkt nicht differenzierbar.

Differenzierbarkeit einer stückweisen Funktion

Sobald wir die Beziehung zwischen Stetigkeit und Differenzierbarkeit einer Funktion kennen, werden wir sehen, wie wir die Differenzierbarkeit einer stückweise definierten Funktion untersuchen können.

Sie können feststellen, ob eine stückweise Funktion an einem Punkt differenzierbar ist, indem Sie die lateralen Ableitungen an diesem Punkt berechnen:

Wenn die lateralen Ableitungen an einem Punkt ungleich sind, ist die Funktion an diesem Punkt nicht differenzierbar:

$f'(x_o^-) \neq f'(x_o^+) \ \longrightarrow$

Es ist nicht abzugsfähig

$x_o$

Wenn die lateralen Ableitungen an einem Punkt zusammenfallen, ist die Funktion an diesem Punkt differenzierbar:

$f'(x_o^-) = f'(x_o^+) \ \longrightarrow$

Ja, es ist differenzierbar in

$x_o$

Hinweis: Damit eine Funktion an einem Punkt differenzierbar ist, muss die Funktion an diesem Punkt stetig sein. Daher müssen wir vor der Berechnung der lateralen Ableitungen sicherstellen, dass die Funktion an diesem Punkt stetig ist. Wenn Sie nicht wissen, wie Kontinuität an einem Punkt untersucht wird, können Sie unter folgendem Link sehen, wie es gemacht wird:

➤ Siehe: Stetigkeit einer Funktion in einem Punkt

Sehen wir uns nun ein Beispiel an, wie man die Ableitung einer Funktion berechnet, die stückweise an einem Punkt definiert ist:

Untersuchen Sie die Stetigkeit und Differenzierbarkeit der folgenden Funktion, die stückweise am Punkt x=2 definiert ist:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.$

Die Funktionen der beiden Teile sind in ihren jeweiligen Intervallen stetig, es muss jedoch geprüft werden, ob die Funktion am kritischen Punkt x=2 stetig ist. Dazu lösen wir die seitlichen Grenzen der Funktion im Punkt:

$\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(3x^2-6x\bigr) = 3\cdot2^2-6\cdot2=12-12=\bm{0}$

$\lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} 6\ln (x-1) = 6\ln (2-1)=6 \ln 1=6 \cdot 0= \bm{0}$

Die seitlichen Grenzen am kritischen Punkt lieferten das gleiche Ergebnis, sodass die Funktion am Punkt x=2 stetig ist.

Sobald wir wissen, dass die Funktion bei x=2 stetig ist, werden wir die Differenzierbarkeit der Funktion an diesem Punkt untersuchen. Dazu berechnen wir die lateralen Ableitungen der in Stücken definierten Funktion:

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.$

Wir bewerten nun jede laterale Ableitung am kritischen Punkt:

$f'(2^-)=6\cdot2-6=12-6 = \bm{6}$

$f'(2^+)=\cfrac{6}{2-1} = \cfrac{6}{1} = \bm{6}$

Die beiden lateralen Ableitungen lieferten das gleiche Ergebnis, sodass die Funktion bei x=2 differenzierbar ist und der Wert der Ableitung 6 beträgt:

$f'(2^-) = f'(2^+) = 6 \ \longrightarrow \ \bm{f'(2) = 6}$

Hätten uns die lateralen Ableitungen andererseits ein anderes Ergebnis geliefert, würde dies bedeuten, dass die Funktion bei x=2 nicht differenzierbar ist. Mit anderen Worten: Die Ableitung würde zu diesem Zeitpunkt noch nicht existieren.

Denken Sie abschließend daran, dass dieses Verfahren auch für die Untersuchung der Differenzierbarkeit einer Absolutwertfunktion gilt, da Absolutwertfunktionen auch stückweise definiert werden können. Hier können Sie sehen, wie Sie eine Absolutwertfunktion in Chunks umwandeln:

➤ Siehe: So definieren Sie stückweise eine Funktion mit einem Absolutwert

Gelöste Übungen zur Differenzierbarkeit einer Funktion

Übung 1

Untersuchen Sie die Stetigkeit und Differenzierbarkeit der folgenden stückweisen Funktion:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.$

Sehen Sie sich die Lösung an

Die Funktionen der beiden Teile sind stetig, wir müssen jedoch prüfen, ob die Funktion am kritischen Punkt x=1 stetig ist. Dazu lösen wir die seitlichen Grenzen der Funktion im Punkt:

$\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^-} \bigl(x^3-4x^2 + 5\bigr)=1^3-4\cdot 1^2 + 5=2$

$\lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1^+} \bigl( -x^2+3x \bigr)=-1^2+3\cdot 1=2$

Die beiden seitlichen Grenzen am kritischen Punkt ergeben das gleiche Ergebnis, sodass die Funktion bei x=1 stetig ist.

Sobald wir wissen, dass die Funktion am kritischen Punkt stetig ist, werden wir untersuchen, ob sie am selben Punkt differenzierbar ist. Wir berechnen daher die lateralen Ableitungen:

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.$

Und wir werten die beiden lateralen Ableitungen bei x=1 aus;

$f'(1^-)=3\cdot1^2-8\cdot 1=3-8=-5$

$f'(1^+)=-2\cdot 1+3=-2+3 =1$

Die lateralen Ableitungen fallen im Punkt x=1 nicht zusammen, sodass die Funktion an diesem Punkt nicht differenzierbar ist.

$f'(1^-) \neq f'(1^+) \ \longrightarrow \ \cancel{\exists} \ f'(1)$

Übung 2

Analysieren Sie die Differenzierbarkeit und Stetigkeit der folgenden in Abschnitten definierten Funktion:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.“ title=“Rendered by QuickLaTeX.com“ height=“65″ width=“226″ style=“vertical-align: 0px;“></p> </p> <div class=$

Sehen Sie sich die Lösung an

Die Funktionen der beiden Abschnitte sind in ihren Intervallen stetig, aber es ist auch notwendig zu wissen, ob die Funktion am kritischen Punkt der Definitionsänderung x=1 stetig ist. Daher definieren wir an dieser Stelle die seitlichen Grenzen der Funktion:

$\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^-} \sqrt{4x} = \sqrt{4\cdot 1} = \sqrt{4}=2$

$\lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1^+} \bigl( 2+\ln x \bigr) = 2 + \ln (1) = 2+0 =2$

Die beiden seitlichen Grenzen am kritischen Punkt ergeben das gleiche Ergebnis, sodass die Funktion bei x=1 stetig ist.

Und jetzt untersuchen wir, ob die Funktion an diesem Punkt differenzierbar ist, indem wir die lateralen Ableitungen berechnen:

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.$

Wir werten die beiden lateralen Ableitungen bei x=1 aus:

$f'(1^-)=\cfrac{4}{2\sqrt{4\cdot1}}=\cfrac{4}{2\sqrt{4}}=\cfrac{4}{2\cdot 2}=\cfrac{4}{4}=1$

$f'(1^+)=\cfrac{1}{1}=1$

Die lateralen Ableitungen sind gleich, daher ist die Funktion bei x=1 differenzierbar und der Wert der Ableitung ist 1.

$f'(1^-) = f'(1^+) = 1 \ \longrightarrow \ \bm{f'(1) = 1}$

Übung 3

Bestimmen Sie, ob die folgende stückweise Funktion über ihren gesamten Bereich stetig und differenzierbar ist:

 *** QuickLaTeX cannot compile formula:
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+1 & \text{si} & x\leq -1 \\[2ex] 2x+2 & \text{ si} & -1<div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E6F9EF" role="button" tabindex="0" aria- expanded="false" data-otfm-spc="#E6F9EF" style="text-align:center"><div class="otfm-sp__title"> <strong>View solution</strong></div>< /div> The functions of all three parts are continuous, but we still need to check if the function is continuous at critical points. We therefore first check the continuity of the function at the point x=-1 by solving the lateral limits at this point:

*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: ...="wp-block-otfm-box-spoiler-start otfm-sp__
Missing { inserted.
leading text: ...ox-spoiler-start otfm-sp__wrapper otfm-sp__
Missing { inserted.
leading text: ...m-sp__wrapper otfm-sp__box js-otfm-sp-box__
Missing { inserted.
leading text: ...fm-sp__box js-otfm-sp-box__closed otfm-sp__
You can't use `macro parameter character #' in math mode.
leading text: ...="0" aria-expanded="false" data-otfm-spc="#
Missing { inserted.
leading text: ...e="text-align:center"><div class="otfm-sp__
Please use \mathaccent for accents in math mode.
leading text: ...g></div></div> The functions of the three parts
Please use \mathaccent for accents in math mode.
leading text: ...are continuous, but we still need to see

\lim\limits_{x\to -1^-} f(x) = \lim\limits_{x\to -1^-} \bigl(x^2+2x+1\bigr) = (-1)^ 2+2(-1)+1 =0 \lim\limits_{x\to -1^+} f(x) = \lim\limits_{x\to -1^+} \bigl(2x+2\bigr ) = 2(-1)+2=0

$Les deux limites latérales au point x=-1 donnent le même résultat, donc la fonction est continue en x=-1. Nous allons maintenant vérifier si la fonction est continue ou non au point x=2 :$

\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(2x+2\bigr) = 2\cdot 2+2=4+2= 6 \lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} \bigl( -x^2+8x\bigr) = -2^2+8\ cdot 2 = -4+16=12

$En revanche, les limites latérales au point x=2 ne donnent pas le même résultat, donc la fonction n'est pas continue en x=2. De plus, comme il n'est pas continu à ce stade, il ne sera pas non plus dérivable à x=2. Une fois que l'on a étudié la continuité de la fonction, on passe à la différentiabilité. On calcule donc les dérivées latérales :$

\displaystyle f'(x)= \left\{ \begin{array}{lcl} 2x+2 & \text{si} & x\leq -1 \\[2ex] 2 & \text{si} & -1

Wir wissen bereits, dass die Funktion bei x=2 nicht differenzierbar ist, also müssen wir nur untersuchen, ob die Funktion bei x=-1 differenzierbar ist. Dazu werten wir die beiden lateralen Ableitungen an der Stelle aus:

$f'(-1^-)=2(-1)+2 = -2+2=0$

$f'(-1^+)=2$

Die lateralen Ableitungen fallen im Punkt x=-1 nicht zusammen, sodass die Funktion an diesem Punkt nicht differenzierbar ist.

$f'(-1^-) \neq f'(-1^+) \ \longrightarrow \ \cancel{\exists} \ f'(-1)$

Übung 4

Berechnen Sie den Wert der Parameter a und b, sodass die folgende stückweise Funktion in ihrem gesamten Bereich stetig und differenzierbar ist:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 2e^{x-3} + a & \text{si} & x< 3 \\[2ex](x-b)^2 & \text{si} & x\geq 3 \end{array} \right.$

Sehen Sie sich die Lösung an

Unabhängig von den Werten der Unbekannten ist die Funktion an allen Punkten stetig und differenzierbar, außer bei x=3, wo ihre Stetigkeit und Differenzierbarkeit überprüft werden muss.

Damit die Funktion an einem Punkt stetig ist, müssen die beiden seitlichen Grenzen an diesem Punkt zusammenfallen. Daher bewerten wir die seitlichen Grenzen am kritischen Punkt:

$\lim\limits_{x\to 3^-} f(x) = \lim\limits_{x\to 3^-} \bigl(2e^{x-3}+a\bigr) = 2e^{3-3}+a = 2 \cdot e^0+a =2\cdot 1 +a = 2+a$

$\lim\limits_{x\to 3^+} f(x) = \lim\limits_{x\to 3^+} (x-b)^2 = (3-b)^2$

Die beiden aus den seitlichen Grenzen erhaltenen Werte müssen daher gleich sein, damit die Funktion stetig ist:

$2+a = (3-b)^2$

Wir analysieren nun die Differenzierbarkeit am Punkt x=3. Wir finden die lateralen Ableitungen:

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.$

Und wir bewerten die beiden lateralen Ableitungen am kritischen Punkt:

$f'(3^-)= 2e^{3-3} = 2e^0 = 2\cdot 1 = 2$

$f'(3^+)=2(3-b) = 6 - 2b$

Damit die Funktion bei x=3 differenzierbar ist, müssen daher die aus den lateralen Ableitungen erhaltenen Werte gleich sein:

$2=6-2b$

Und indem wir diese Gleichung lösen, können wir den Wert von b ermitteln:

$2b=6-2$

$2b=4$

$b=\cfrac{4}{2} =\bm{2}$

Sobald wir schließlich den Wert des Parameters b kennen, können wir den Wert des Parameters a berechnen, indem wir die Gleichung lösen, die wir zuvor in den seitlichen Grenzen erhalten haben:

$2+a = (3-b)^2$

$2+a = (3-2)^2$

$2+a =1$

$a =1-2$

$\bm{a =-1}$

Differenzierbarkeit und Stetigkeit einer Funktion

Differenzierbarkeit einer stückweisen Funktion

Gelöste Übungen zur Differenzierbarkeit einer Funktion

Übung 1

Übung 2

Übung 3

Übung 4

Kommentar verfassen Kommentieren abbrechen