Diagonalmatrix - Mathematik

Auf dieser Seite sehen Sie, was eine Diagonalmatrix ist und Beispiele für Diagonalmatrizen. Darüber hinaus erfahren Sie, wie Sie mit dieser Art von Matrizen arbeiten, wie Sie ihre Determinanten einfach berechnen und wie Sie sie invertieren. Es gibt auch Eigenschaften und Anwendungen von Diagonalmatrizen. Und schließlich gibt es noch die Erklärungen einer bidiagonalen Matrix und einer tridiagonalen Matrix.

Was ist eine Diagonalmatrix?

Eine Diagonalmatrix ist eine quadratische Matrix, in der alle Elemente, die nicht auf der Hauptdiagonale liegen, Null (0) sind. Die Elemente der Hauptdiagonale können Null sein oder auch nicht.

Sobald wir die genaue Definition einer Diagonalmatrix kennen, werden wir Beispiele für Diagonalmatrizen sehen:

Beispiele für Diagonalmatrizen

Beispiel einer Diagonalmatrix der Dimension 2 × 2

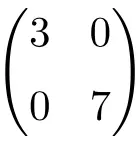
Beispiel einer Diagonalmatrix der Ordnung 3×3

Beispiel einer Diagonalmatrix der Größe 4×4

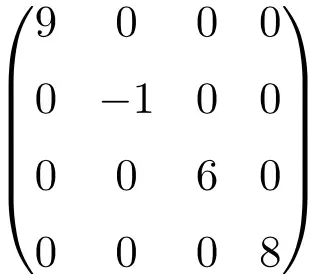
Diese Arten von Matrizen werden im Allgemeinen unter Angabe der Elemente der Diagonale geschrieben:

$diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Operationen mit Diagonalmatrizen

Einer der Gründe, warum Diagonalmatrizen für die lineare Algebra so wichtig sind, liegt in der Einfachheit, mit der sie Berechnungen durchführen können. Deshalb werden sie in der Mathematik so häufig verwendet.

Diagonalmatrizen addieren und subtrahieren

Das Addieren (und Subtrahieren) zweier Diagonalmatrizen ist sehr einfach: Addieren (oder subtrahieren) Sie einfach die Zahlen auf den Diagonalen.

$\displaystyle \text{diag}(a_1,... ,a_n) \pm \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\pm b_1,..., a_n\pm b_n)$

Zum Beispiel:

$\displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

Diagonalmatrixmultiplikation

Um eine Multiplikation oder ein Matrixprodukt zweier Diagonalmatrizen zu lösen, multiplizieren Sie einfach die Elemente der Diagonalen miteinander.

$\displaystyle \text{diag}(a_1,... ,a_n) \cdot \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\cdot b_1,..., a_n\cdot b_n)$

Zum Beispiel:

$\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}$

Potenz diagonaler Matrizen

Um die Potenz einer Diagonalmatrix zu berechnen, müssen wir jedes Element der Diagonale auf den Exponenten erhöhen:

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle A^k= \text{diag}(a_1^k,... ,a_n^k)$

Zum Beispiel:

$\displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}$

Determinante einer Diagonalmatrix

Die Determinante einer Diagonalmatrix ist das Produkt der Elemente auf der Hauptdiagonale.

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

Schauen Sie sich die folgende gelöste Übung an, in der wir die Determinante einer Diagonalmatrix einfach durch Multiplikation der Elemente ihrer Hauptdiagonale ermitteln:

$\displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30$

Dieser Satz ist leicht zu beweisen: Sie müssen lediglich die Determinante einer Diagonalmatrix anhand von Blöcken (oder Cofaktoren) berechnen. Diese Demonstration wird unten anhand einer generischen Diagonalmatrix detailliert beschrieben:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}$

Kehren Sie eine Diagonalmatrix um

Eine Diagonalmatrix ist genau dann invertierbar, wenn alle Elemente der Hauptdiagonale von 0 verschieden sind . In diesem Fall sagen wir, dass die Diagonalmatrix eine reguläre Matrix ist.

Darüber hinaus ist die Umkehrung einer Diagonalmatrix immer eine andere Diagonalmatrix mit den Umkehrungen der Hauptdiagonale:

$\displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}$

Aus der vorherigen Charakteristik können wir ableiten, dass die Determinante der Umkehrung einer Diagonalmatrix das Produkt der Umkehrungen der Hauptdiagonale ist:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{4} \cdot \cfrac{1}{-1}=-\cfrac{1}{8} = -0,125$

Eigenschaften von Diagonalmatrizen

Jede Diagonalmatrix ist auch eine symmetrische Matrix .

Eine Diagonalmatrix ist eine Matrix, die sowohl obere als auch untere Dreiecksform hat .

Die Identitätsmatrix ist eine Diagonalmatrix:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Ebenso ist die Nullmatrix auch eine Diagonalmatrix, da alle ihre Elemente, die nicht auf der Diagonale liegen, Nullen sind. Obwohl die Zahlen auf der Diagonale 0 sind.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Die Eigenwerte (oder Eigenwerte) einer Diagonalmatrix sind die Elemente ihrer Hauptdiagonale.

$\begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7$

Eine quadratische Matrix ist genau dann diagonal, wenn sie dreieckig und normal ist.

Der Adjungierte einer Diagonalmatrix ist eine weitere Diagonalmatrix.

Diagonalmatrix-Anwendungen

Wie wir gesehen haben, ist das Lösen von Berechnungen mit Diagonalmatrizen sehr einfach, da viele Nullstellen an den Operationen beteiligt sind. Aus diesem Grund sind sie im Bereich der Mathematik sehr nützlich und werden häufig verwendet.

Aus demselben Grund wurden so viele Studien zur Diagonalisierung einer Matrix durchgeführt und tatsächlich wurde sogar eine Methode zur Diagonalisierung von Matrizen entwickelt (unter Verwendung des charakteristischen Polynoms).

Daher sind auch diagonalisierbare Matrizen durchaus relevant. Wie der Spektralzerlegungssatz, der die Bedingungen dafür festlegt, wann eine Matrix diagonalisiert werden kann und wann nicht.

bidiagonale Matrix

Eine bidiagonale Matrix ist eine quadratische Matrix, in der alle Elemente, die nicht auf der Hauptdiagonale oder auf der oberen oder unteren Diagonale liegen, 0 sind.

Zum Beispiel:

$\begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}$

obere bidiagonale Matrix

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}$

untere bidiagonale Matrix

Wenn die Hauptdiagonale und die erste Superdiagonale besetzt sind, spricht man von einer oberen Bidiagonalenmatrix. Sind hingegen die Hauptdiagonale und die erste Unterdiagonale besetzt, spricht man von einer unteren Bidiagonalenmatrix.

tridiagonale Matrix

Eine tridiagonale Matrix ist eine quadratische Matrix, deren einzige von Null verschiedene Elemente die der Hauptdiagonalen und der angrenzenden Diagonalen darüber und darunter sind.

Zum Beispiel:

$\begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}$

Somit sind alle Diagonal-, Bidiagonal- und Tridiagonalmatrizen Beispiele für Bandmatrizen . Denn eine Bandmatrix ist diejenige Matrix, deren alle von Null verschiedenen Elemente um die Hauptdiagonale liegen.

Diagonale matrix

Was ist eine Diagonalmatrix?

Beispiele für Diagonalmatrizen

Operationen mit Diagonalmatrizen

Diagonalmatrizen addieren und subtrahieren

Diagonalmatrixmultiplikation

Potenz diagonaler Matrizen

Determinante einer Diagonalmatrix

Kehren Sie eine Diagonalmatrix um

Eigenschaften von Diagonalmatrizen

Diagonalmatrix-Anwendungen

bidiagonale Matrix

tridiagonale Matrix

Kommentar verfassen Kommentieren abbrechen