Was sind dezimalzahlen?

Dezimalzahlen haben in der mathematischen Welt eine große Bedeutung, aber wissen wir wirklich, was sie sind und wie sie funktionieren? In diesem Artikel erklären wir Ihnen alles.

Was sind Dezimalzahlen?

Dezimalzahlen sind nicht ganzzahlige Zahlen (nicht in der Ganzzahlmenge enthalten), die aus einem ganzzahligen Teil und einem Dezimalteil bestehen. Dieser Dezimalteil wird nach einem Komma geschrieben und ermöglicht die Darstellung von Werten kleiner als Eins.

Dezimalzahlen sind eine Möglichkeit, gemischte Zahlen darzustellen. Tatsächlich ist das Konzept des Bruchs dem des Dezimalwerts ziemlich ähnlich. Wir können dies im folgenden Beispiel sehen: 7/2 ist gleich 3,5 . Sie behalten ihre numerische Äquivalenz bei, nur dass sie unterschiedlich geschrieben werden.

Die Zahl „3,5“ ist eine Dezimalzahl, die sich als „drei Komma fünf“ liest, ihr ganzzahliger Teil ist 3 und ihr dezimaler Teil ist gleich 5. Da Dezimalzahlen mit dem Dezimalschreibsystem ausgedrückt werden, können wir die Zahl wie folgt zerlegen :

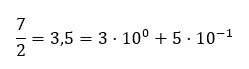
Dezimalnomenklatur

Beim Schreiben dieser Zahlen werden üblicherweise zwei Arten der Notation verwendet: die Standardnotation (oder Dezimalnotation) und die wissenschaftliche Notation . Das erste ist das gebräuchlichste und das, das wir bisher verwendet haben.

Während die wissenschaftliche Notation eine abgekürzte Form der Standardnotation ist. In der wissenschaftlichen Schreibweise wird eine Dezimalzahl als ganze Zahl multipliziert mit einer Zehnerpotenz geschrieben. Beispielsweise kann die Größe 0,0054 in wissenschaftlicher Schreibweise als 5,4 · 10 ^-3 geschrieben werden.

Was die nicht-numerische Schreibweise von Dezimalzahlen betrifft, verwenden wir eine Notation, die sich auf die Position bezieht, die jede Dezimalstelle einnimmt. Nun, genau wie der ganzzahlige Teil hat: die Einheit, die Zehn, den Hundert … Der dezimale Teil hat: das Zehntel, das Hundertstel, das Tausendstel …

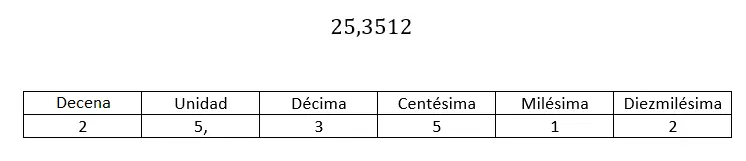
Was den Namen jeder Ziffer kennzeichnet, ist die Position, die sie im Verhältnis zum Dezimalpunkt einnimmt. Wenn Sie also eine Dezimalzahl haben und den Wert des Hundertstels wissen möchten, müssen Sie sich die zweite Ziffer ansehen (vom Dezimalpunkt nach rechts). Im obigen Fall ist das Hundertstel gleich 5.

Arten von Dezimalzahlen

Dezimalzahlen können wie folgt klassifiziert werden:

• Exakte Dezimalzahl: hat eine bestimmte und endliche Anzahl von Dezimalstellen. Beispiel: 9.263.
• Wiederkehrende Dezimalzahl: hat unendlich viele Dezimalstellen.
  • Reine sich wiederholende Dezimalzahl: Der Dezimalteil besteht aus einer Zahl, die sich unendlich wiederholt. Zum Beispiel: 2.1515151515… Seit 15 Wiederholungen auf unbestimmte Zeit.
  • Gemischte sich wiederholende Dezimalzahl: Der Dezimalteil besteht aus einem Wert, gefolgt von einer weiteren Zahl, die sich unendlich wiederholt. Zum Beispiel: 2.4615151515… Da sich 46 nicht wiederholt.
• Sich nicht wiederholende Dezimalzahl: hat einen unendlichen Dezimalteil, der sich nicht wiederholt. In diesem Abschnitt finden wir einige mathematische Konstanten , die Quadratwurzel aus zwei…

Eigenschaften von Dezimalzahlen

Dezimalzahlen haben mehrere Eigenschaften, darunter:

• Eine Dezimalzahl ändert sich nicht, wenn rechts Nullen hinzugefügt werden, daher entspricht die Zahl 0,25 0,250 und 0,2500. Im Grunde, weil sie den gleichen Betrag ausdrücken.
• Dezimalstellen entsprechen Brüchen, beispielsweise wird eine halbe Einheit (1/2) durch 0,5 dargestellt.
• Wenn wir eine Dezimalzahl mit Zehnerpotenzen multiplizieren oder dividieren, müssen wir den Dezimalpunkt verschieben: nach rechts, wenn wir multiplizieren, und nach links, wenn wir dividieren.

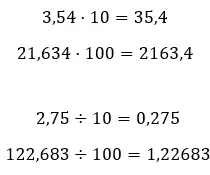
• Sie können eine Dezimalzahl vereinfachen, indemSie die Dezimalzahlen runden . Diese Methode besteht darin, weniger Dezimalstellen auszudrücken und den Wert der Zahl so wenig wie möglich zu verändern. Wenn Sie lernen möchten, wie Sie dieses Vereinfachungssystem verwenden, empfehlen wir Ihnen, diesen letzten Link einzugeben.

Darstellung von Dezimalzahlen

Die Dezimalmenge lässt sich wie alle anderen Mengen auf dem Zahlenstrahl darstellen.

Ausgehend von der Tatsache, dass Dezimalzahlen einen ganzzahligen Teil und eine Dezimalstelle (kleiner als Eins) haben, können wir ableiten, dass Dezimalzahlen zwischen ganzen Zahlen dargestellt werden. Beispielsweise gibt es zwischen der Zahl 0 und 1 unendlich viele Nachkommastellen. Unten können Sie es in der Zeile dargestellt sehen:

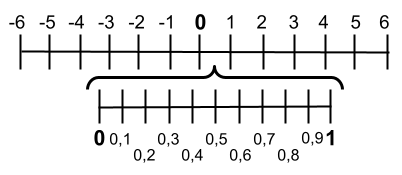
Wie Sie im Bild sehen können, haben wir die Zehntel zwischen 0 und 1 geschrieben. Obwohl es zwischen diesen beiden Zahlen unendlich viele Nachkommastellen gibt, können sehr komplexe Darstellungen gemacht werden. Darüber hinaus geschieht dies nicht nur zwischen 0 und 1, sondern zwischen allen ganzen Zahlen.

Operationen mit Dezimalzahlen

Die Operationen von Dezimalzahlen ähneln denen von ganzen Zahlen. Der einzige Unterschied besteht darin, dass die Dezimalstellen berücksichtigt werden müssen. Bevor Sie eine Operation lösen, müssen Sie daher sicherstellen, dass Sie immer mit den gleichen Zahlen arbeiten: Zehntel mit Zehntel, Hundertstel mit Hundertstel …

Als nächstes geben wir einen kurzen Überblick über die vier grundlegenden arithmetischen Operationen mit Dezimalzahlen:

• Addition von Dezimalstellen:

• Subtraktion von Dezimalzahlen:

• Multiplikation von Dezimalzahlen:

• Dezimaldivision:

Verwendung und Anwendungen von Dezimalzahlen

Dezimalzahlen werden im Alltag und in der Mathematik häufig verwendet. Wenn Sie beispielsweise etwas in einem Geschäft kaufen , müssen Sie den Preis dafür kennen, was Sie kaufen, und dieser Preis wird in Dezimalzahlen ausgedrückt. Darüber hinaus werden sie zur Messung von Entfernungen, Gewichten und anderen Aspekten des täglichen Lebens verwendet.

In der Mathematik ermöglichen uns Dezimalzahlen, sehr kleine oder sehr große Mengen einfach auszudrücken. Und sie ermöglichen uns auch eine präzisere Berechnung. Wenn wir beispielsweise die Hälfte von 3 Einheiten berechnen möchten, können wir sie in zwei gleiche Teile teilen und erhalten 1,5 Einheiten.