Berechnen Sie die Determinante einer 3x3-Matrix mit der Regel von Sarrus

Auf dieser Seite erfahren Sie, was die Determinante einer 3×3-Quadratmatrix ist. Sie erfahren, wie Sie die Determinanten der Ordnung 3 mithilfe der Sarrus-Regel lösen. Und zusätzlich werden Ihnen Beispiele und Übungen Schritt für Schritt gelöst, sodass Sie es perfekt üben und verstehen können.

Was ist die Determinante einer 3×3-Matrix?

Eine Determinante der Ordnung 3 ist eine Matrix der Dimension 3×3 , die durch einen vertikalen Balken auf jeder Seite der Matrix dargestellt wird. Wenn wir zum Beispiel die folgende Matrix haben:

$\displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}$

Die Determinante der Matrix A wird wie folgt dargestellt:

$\displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}$

Wie Sie gesehen haben, ist es einfach, die Determinante einer quadratischen Matrix der Ordnung 3 zu schreiben. Sehen wir uns nun an, wie man das Problem löst:

Wie berechnet man eine Determinante der Ordnung 3?

Um die Determinanten von 3×3-Matrizen zu ermitteln, müssen Sie die Regel von Sarrus anwenden:

Sarrus-Herrschaft

Die Regel von Sarrus besagt, dass wir zur Berechnung einer Determinante der Ordnung 3 das Produkt der Elemente der Hauptdiagonale und das Produkt ihrer parallelen Diagonalen mit ihren entsprechenden gegenüberliegenden Eckpunkten addieren und dann das Produkt der Elemente der Nebendiagonale subtrahieren müssen das Produkt ihrer parallelen Diagonalen mit ihren entsprechenden gegenüberliegenden Eckpunkten.

So geschrieben kann es etwas schwierig sein, es zu verstehen, aber sehen Sie sich anhand des folgenden Diagramms und der Beispiele an, wie die Berechnung von 3×3-Determinanten erfolgt:

Beispiele für 3×3-Determinanten:

$\begin{aligned} \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} & = 2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + (-1) \cdot 4 \cdot 3 - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- (-1) \cdot 1 \cdot 1 \\ & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & = \bm{-3} \end{aligned}$

$\begin{aligned} \begin{vmatrix} 1 & 0 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 4 & -3 & -1 \end{vmatrix} & = 1\cdot 2 \cdot (-1) + 0 \cdot 1 \cdot 4 +3 \cdot (-3) \cdot 2 - 4 \cdot 2 \cdot 2 - (-3) \cdot 1 \cdot 1- 3 \cdot 0 \cdot (-1) \\ & = -2 +0 -18 - 16 +3- 0 \\[2ex] & = \bm{-33} \end{aligned}$

Probleme der Determinanten von 3 × 3-Matrizen gelöst

Übung 1

Lösen Sie die folgende 3×3-Determinante:

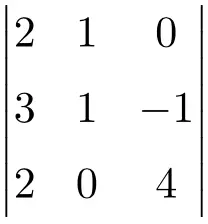
Konkretes Beispiel für die Determinante einer 3x3-Matrix

siehe Lösung

Um die Determinante einer 3×3-Matrix zu lösen, müssen wir die Regel von Sarrus anwenden:

$\displaystyle\begin{aligned} \begin{vmatrix} 2 & 1 & 0 \\[1.1ex] 3 & 1 & -1 \\[1.1ex] 2 & 0 & 4 \end{vmatrix} & = 2 \cdot 1 \cdot 4 + 1 \cdot (-1) \cdot 2 + 3 \cdot 0 \cdot 0 - 2 \cdot 1 \cdot 0 - 0 \cdot (-1) \cdot 2- 3 \cdot 1 \cdot 4 \\ & = 8 -2 +0 -0- 0-12 \\[2ex] & = \bm{-6} \end{aligned}$

Übung 2

Berechnen Sie die folgende Determinante der Ordnung 3:

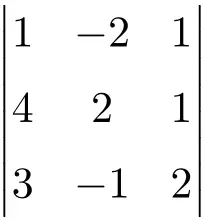
Schritt für Schritt gelöste Übung zur Determinante einer 3x3-Matrix

siehe Lösung

Um die Determinante einer Matrix dritter Ordnung zu berechnen, müssen wir die Regel von Sarrus verwenden:

$\displaystyle\begin{aligned} \begin{vmatrix} 1 & -2 & 1 \\[1.1ex] 4 & 2 & 1 \\[1.1ex] 3 & -1 & 2 \end{vmatrix} & = 1 \cdot 2 \cdot 2 + (-2) \cdot 1 \cdot 3 + 4 \cdot (-1) \cdot 1 - 3 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot 1 - 4 \cdot (-2) \cdot 2 \\ & = 4 -6 -4 -6+1+16 \\[2ex] & = \bm{5} \end{aligned}$

Übung 3

Finden Sie die Lösung für die Determinante der folgenden 3×3-Matrix:

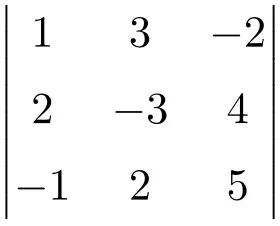
Schritt für Schritt gelöste Übungen für Determinanten von 3x3-Matrizen

siehe Lösung

Um eine Determinante einer 3×3-Matrix zu erstellen, müssen wir die Regel von Sarrus verwenden:

$\displaystyle\begin{aligned} \begin{vmatrix}1 & 3 & -2 \\[1.1ex] 2 & -3 & 4 \\[1.1ex] -1 & 2 & 5 \end{vmatrix} & = \\ & = 1 \cdot (-3) \cdot 5 + 3 \cdot 4 \cdot (-1) + 2 \cdot 2 \cdot (-2) \ - \\[1.1ex] & \phantom{=} - (-1) \cdot (-3) \cdot (-2) - 2 \cdot 4 \cdot 1 - 2 \cdot 3 \cdot 5 \\[2.5ex] & = -15 -12 -8 +6-8-30 \\[2.5ex] & = \bm{-67} \end{aligned}$

Übung 4

Finden Sie die Lösung für die Determinante der folgenden Matrix der Ordnung 3:

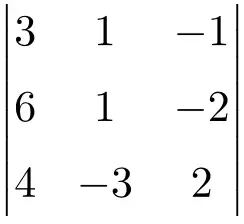
Gelöste Übung zu einer Determinante einer 3x3-Matrix

siehe Lösung

Um die Lösung einer Determinante einer 3×3-Matrix zu finden, müssen wir die Sarrus-Formel anwenden:

$\displaystyle\begin{aligned} \begin{vmatrix} 3 & 1 & -1 \\[1.1ex] 6 & 1 & -2 \\[1.1ex] 4 & -3 & 2 \end{vmatrix} & = \\ & = 3 \cdot 1 \cdot 2 + 1 \cdot (-2) \cdot 4 + 6 \cdot (-3) \cdot (-1) \ - \\[1.1ex] & \phantom{=} - 4 \cdot 1 \cdot (-1) - (-3) \cdot (-2) \cdot 3 - 6 \cdot 1 \cdot 2 \\[2.5ex] & =6 -8 +18 +4-18-12 \\[2.5ex] & = \bm{-10} \end{aligned}$

Übung 5

Finden Sie den Wert von

$a$

was die folgende Determinante dritter Ordnung aufhebt:

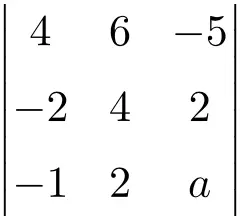
Schritt für Schritt gelöste Übungen für Determinanten der Ordnung 3

siehe Lösung

Wir berechnen zunächst mit der Sarrus-Regel den Wert der Determinante als Funktion von

$a :$

$\displaystyle\begin{aligned}\begin{vmatrix} 4 & 6 & -5 \\[1.1ex] -2 & 4 & 2 \\[1.1ex] -1 & 2 & a \end{vmatrix} & = \\ & = 4 \cdot 4 \cdot a + 6 \cdot 2 \cdot (-1) + (-2) \cdot 2 \cdot (-5) \ - \\[1.1ex] & \phantom{=}- (-1) \cdot 4 \cdot (-5) - 2 \cdot 2 \cdot 4 - (-2) \cdot 6 \cdot a \\[2.5ex] & = 16a -12 + 20 - 20 - 16 +12a \\[2.5ex] & = 28a -28 \end{aligned}$

Damit die Determinante verschwindet, muss das Ergebnis 0 sein. Daher setzen wir das Ergebnis gleich 0 und lösen die Gleichung:

$28a-28=0$

$28a=28$

$a=\cfrac{28}{28} = \bm{1}$

Berechnen sie die determinante einer 3×3-matrix mit der sarrus-regel

Was ist die Determinante einer 3×3-Matrix?

Wie berechnet man eine Determinante der Ordnung 3?

Sarrus-Herrschaft

Beispiele für 3×3-Determinanten:

Probleme der Determinanten von 3 × 3-Matrizen gelöst

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Kommentar verfassen Kommentieren abbrechen