Auf dieser Seite finden Sie alles über senkrechte Linien: Was sie sind, wann zwei Linien senkrecht zueinander stehen, wie man eine Linie senkrecht zu einer anderen berechnet, ihre Eigenschaften usw. Außerdem können Sie sich Beispiele ansehen und dies tun Üben Sie mit Schritt für Schritt gelösten Übungen.
Was sind zwei senkrechte Linien?
In der Mathematik sind zwei Geraden senkrecht, wenn sie sich in einem Punkt schneiden, der vier gleiche rechte Winkel (90°) bildet.

Zusätzlich müssen auch die Richtungsvektoren zweier senkrechter Linien senkrecht zueinander stehen.
Die Rechtwinkligkeit zweier Linien wird im Allgemeinen durch das Symbol angezeigt
![]()
Denken Sie andererseits daran, dass es in der Ebene vier Möglichkeiten für das Konzept der relativen Position zwischen zwei Linien gibt: Zwei Linien können sekant, senkrecht, zusammenfallend oder parallel sein. Wenn Sie möchten, können Sie die Bedeutung der einzelnen Zeilentypen auf unserer Website überprüfen.
Woher wissen Sie, ob zwei Linien senkrecht zueinander stehen?
Es gibt zwei Möglichkeiten, zu bestimmen, ob zwei Linien senkrecht zueinander stehen: anhand ihrer Richtungsvektoren oder anhand ihrer Steigungen . Nachfolgend finden Sie eine Erläuterung beider Methoden. Obwohl sie demselben Zweck dienen, empfehlen wir Ihnen, zu wissen, wie beide Verfahren durchgeführt werden, da jede davon davon abhängt, wie die Linien ausgedrückt werden.
Aus den Richtungsvektoren der Linien
Eine Möglichkeit herauszufinden, wann zwei Linien senkrecht zueinander stehen, besteht darin, die Richtungsvektoren der betreffenden Linien zu verwenden. Denken Sie daran, dass der Richtungsvektor der Vektor ist, der die Richtung einer Linie angibt.
Auch die Richtungsvektoren zweier senkrechter Geraden stehen zueinander orthogonal. Wenn also das Skalarprodukt der Richtungsvektoren zweier Linien gleich 0 ist, bedeutet dies, dass die Linien senkrecht zueinander stehen.
![]()
Sehen wir uns anhand eines Beispiels an, wie die Rechtwinkligkeit zweier Geraden bestimmt wird:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bad2c42aa92c183e085434ccb23cc2_l3.png)
Beide Linien werden als parametrische Gleichungen ausgedrückt, sodass die Komponenten des Richtungsvektors jeder Linie die Zahlen vor dem Parameter sind
![]()
![]()
Sobald wir den Richtungsvektor jeder Linie kennen, prüfen wir, ob sie senkrecht sind, indem wir das Produkt zwischen den Vektoren berechnen:
![]()
Das Skalarprodukt der beiden Vektoren ist Null, die Geraden stehen also senkrecht zueinander.
Linienpisten
Eine andere Möglichkeit, festzustellen, ob zwei Geraden senkrecht zueinander stehen, besteht darin, ihre Steigungen zu verwenden. Denken Sie daran, dass die Steigung einer Geraden der Koeffizient ist
![]()
der expliziten Gleichung und der Punkt-Steigungsgleichung einer Geraden.
![]()
Und auch die Steigung einer Geraden lässt sich aus den Koeffizienten ermitteln
![]()
Und
![]()
der impliziten (oder allgemeinen) Gleichung einer Geraden:
![]()
Somit sind die Steigungen zweier senkrechter Geraden umgekehrt und haben entgegengesetztes Vorzeichen, d. h. die folgende Gleichheit ist immer erfüllt:
![]()
Wenn also das Produkt der Steigungen zweier verschiedener Geraden gleich -1 ist, bedeutet dies, dass die Geraden senkrecht zueinander stehen:
![]()
Beispielsweise stehen die folgenden zwei Geraden senkrecht aufeinander:
![]()
Anhand ihrer Steigungen können wir zeigen, dass es sich um zwei senkrecht zueinander stehende Geraden handelt. Die Steigung jeder Geraden beträgt:
![]()
Jetzt multiplizieren wir die Steigungen:
![]()
Das Produkt zwischen den beiden Steigungen entspricht -1, was eigentlich zwei senkrecht zueinander stehende Geraden bedeutet.
Wie berechnet man eine Linie senkrecht zu einer anderen?
Obwohl es schwierig erscheinen mag, ist das Finden einer Linie senkrecht zu einer anderen recht einfach. Dazu benötigen Sie lediglich einen Richtungsvektor senkrecht zur Linie und einen Punkt, der zur Linie gehört.
Die einzige Schwierigkeit besteht darin, dass das Verfahren wie zuvor von der Art der Gleichung abhängt, in der die Linien ausgedrückt werden. Denn eine Gerade senkrecht zu einer anderen lässt sich aus den Richtungsvektoren oder aus den Steigungen berechnen.
Vom Richtungsvektor nach rechts
Eine Linie senkrecht zu einer anderen gegebenen Linie kann anhand ihres Richtungsvektors gefunden werden. Sehen wir uns anhand eines Beispiels an, wie das geht:
- Berechnen Sie die Linie senkrecht zur Linie

was durch den Punkt geht
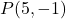
. gerade sein

![]()
Als erstes müssen wir den Richtungsvektor der Linie identifizieren. In diesem Fall wird die Linie in Form einer allgemeinen (oder impliziten) Gleichung definiert, daher können die kartesischen Koordinaten des Richtungsvektors der Linie mit den Koeffizienten A und B der Linie erhalten werden:
![]()
Und sobald wir den Richtungsvektor der Linie kennen, müssen wir einen Vektor senkrecht dazu berechnen. Geben Sie dazu einfach die Koordinaten des Vektors ein und ändern Sie das Vorzeichen eines davon (des gewünschten):
![]()
Jetzt kennen wir den Richtungsvektor der Linie. Die implizite Gleichung der Geraden lautet daher wie folgt:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7a24d8f41b3c82e25a2a64fed8dc6eb6_l3.png)
![]()
Daher reicht es aus, den Parameter C zu bestimmen. Dazu setzen wir den Punkt, der zur Geraden gehört, in ihre Gleichung ein und lösen die resultierende Gleichung:
![]()
![]()
![]()
![]()
![]()
Zusammenfassend lautet die Gleichung der Senkrechten:
![]()
Von der Steigung der Linie
Eine andere Möglichkeit, eine Gerade senkrecht zu einer bestimmten Geraden zu finden, ist die Messung ihrer Steigung. Sehen wir uns anhand eines Beispiels an, wie diese Art von Problem gelöst wird:
- Berechnen Sie die Linie senkrecht zur Linie

was durch den Punkt geht
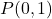
. gerade sein

![]()
Die Steigung der Linie
![]()
Ost:
![]()
Sobald wir die Steigung der Geraden kennen, müssen wir die Steigung der senkrechten Geraden ermitteln. Wie wir in den Abschnitten oben gesehen haben, sind die Steigungen zweier senkrechter Linien umgekehrt und ihr Vorzeichen ändert sich. Um die Steigung der Senkrechten zu bestimmen, müssen wir daher die gefundene Steigung umkehren und ihr Vorzeichen ändern:
![]()
Die explizite Gleichung der Senkrechten lautet daher wie folgt:
![]()
![]()
Schließlich berechnen wir die Ordinate im Ursprung der Senkrechten, indem wir die Koordinaten des Punktes in die Geradengleichung einsetzen:
![]()
![]()
![]()
Kurz gesagt lautet die Gleichung der Senkrechten:
![]()
Eigenschaften senkrechter Linien
Alle senkrechten Linien haben die folgenden Eigenschaften:
- Symmetrische Beziehung : Wenn eine Linie senkrecht zu einer anderen Linie steht, steht diese Linie auch senkrecht zur ersten Linie.
![]()
- Nichtreflexive Eigenschaft : Offensichtlich kann keine Linie senkrecht zu sich selbst sein.
![]()
- Satz: In der euklidischen Geometrie (im R2) muss jedes Paar von Geraden, die senkrecht zu einer dritten Geraden stehen, notwendigerweise parallel sein. Das heißt, wenn eine Linie senkrecht zu einer anderen Linie steht und diese Linie auch senkrecht zu einer dritten Linie ist, sind die erste und die letzte Linie parallel.
Probleme mit senkrechten Linien gelöst
Übung 1
Welche der folgenden Geraden stehen senkrecht zur Geraden?
![]()
?
![]()
![]()
![]()
![]()
![]()
Die Steigung der Linie
![]()
ist 3:
![]()
Und die Steigungen zweier senkrechter Geraden sind umgekehrt und haben entgegengesetztes Vorzeichen, also die Steigung jeder Geraden senkrecht zur Geraden
![]()
muss sein:
![]()
Damit die Linien senkrecht zur Linie stehen
![]()
sind diejenigen, deren Steigung gleich ist
![]()
. Das heißt, die Zeilen
![]()
Und
![]()
Übung 2
Bestimmen Sie, ob die folgenden zwei Linien senkrecht zueinander stehen:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e9d2323afa87c41dec84f29a4c5d645_l3.png)
das Recht
![]()
wird in Form einer parametrischen Gleichung ausgedrückt, sodass die Komponenten des Richtungsvektors dieser Geraden die Zahlen vor dem Parameter sind
![]()
![]()
Andererseits die gerade Linie
![]()
ist in Form einer kontinuierlichen Gleichung definiert, daher sind die Koordinaten seines Richtungsvektors die Zahlen der Nenner:
![]()
Sobald wir den Richtungsvektor jeder Linie kennen, können wir überprüfen, ob sie senkrecht zueinander stehen, indem wir das Produkt der beiden Vektoren berechnen:
![]()
Das Skalarprodukt der beiden Vektoren ist ungleich Null, daher stehen die Geraden nicht senkrecht zueinander .
Übung 3
Finden Sie die Linie senkrecht zur Linie
![]()
was durch den Punkt geht
![]()
. gerade sein
![]()
![]()
Als erstes müssen wir den Richtungsvektor der Linie identifizieren. In diesem Fall wird die Linie in Form einer allgemeinen (oder impliziten) Gleichung definiert, sodass ihr Richtungsvektor lautet:
![]()
Sobald wir den Richtungsvektor der Linie kennen, müssen wir einen Vektor senkrecht dazu berechnen. Geben Sie dazu einfach die Koordinaten des Vektors ein und ändern Sie das Vorzeichen eines davon (des gewünschten):
![]()
Die implizite Gleichung der Geraden lautet daher wie folgt:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8833b30c014bab389b6df773ac4c4ea2_l3.png)
![]()
Es reicht also aus, die Unbekannte C zu bestimmen. Dazu setzen wir den Punkt, durch den die Gerade geht, in ihre Gleichung ein:
![]()
![]()
![]()
![]()
![]()
Schließlich lautet die Gleichung der Senkrechten:
![]()
Übung 4
Finden Sie die Punkt-Steigungsgleichung der Geraden senkrecht zur Geraden
![]()
was durch den Punkt geht
![]()
. gerade sein
![]()
![]()
Die Steigung der Linie
![]()
Ost:
![]()
Sobald wir die Steigung der Geraden kennen, müssen wir die Steigung der senkrechten Geraden ermitteln. Dazu kehren Sie einfach die gefundene Steigung um und ändern ihr Vorzeichen:
![]()
Zum Schluss setzen Sie einfach die gefundene Steigung und die Koordinaten des Punktes in die Punkt-Steigungsgleichung der Geraden ein:
![]()
![]()
![]()
Übung 5
das Recht
![]()
geht durch die Punkte (2,1) und (4,2) und die Gerade
![]()
geht durch die Punkte (-1,2) und (1,-2). Bestimmen Sie, ob es sich um zwei senkrechte Linien handelt oder nicht.
Um zu überprüfen, ob es sich um zwei senkrechte Linien handelt, berechnen wir ihre Steigungen und prüfen dann, ob sie die senkrechte Beziehung respektieren. Denken Sie daran, dass die Formel für die Steigung einer Geraden lautet:
![]()
Die Steigung der Linie
![]()
Ost:
![]()
Die Steigung der Linie
![]()
Ost:
![]()
Um die Rechtwinkligkeit der beiden Geraden zu prüfen, müssen wir prüfen, ob die Steigung einer Geraden umgekehrt zur anderen Steigung ist. In diesem Fall sind die beiden Steigungen umgekehrt und haben auch entgegengesetzte Vorzeichen, sodass die beiden Geraden senkrecht zueinander stehen.
Übung 6
Berechnen Sie den Wert von
![]()
so dass die folgenden zwei Geraden senkrecht zueinander stehen:
![]()
Die beiden Linien werden in Form einer impliziten (oder allgemeinen) Gleichung ausgedrückt, und der Richtungsvektor einer impliziten Gleichung der Linie ist:
![]()
![]()
Daher wäre der Richtungsvektor jeder Linie:
![]()
Damit zwei Geraden senkrecht zueinander stehen, muss das Skalarprodukt ihrer Richtungsvektoren Null sein. Daher werden wir diese Bedingung anwenden, um den Wert der Unbekannten zu ermitteln
![]()
![]()
![]()
![]()
![]()
![]()
![]()