Parallele Linien

Hier erfahren Sie alles über parallele Linien: was sie bedeuten, wie man bestimmt, ob zwei Linien parallel sind, ihre Eigenschaften usw. Darüber hinaus können Sie sich mehrere Beispiele und gelöste Übungen zu parallelen Linien ansehen.

Was sind parallele Linien?

Parallele Linien sind Linien, die sich niemals kreuzen, das heißt, selbst wenn ihre Flugbahnen bis ins Unendliche ausgedehnt werden, berühren sie sich nie. Daher haben die Punkte zweier paralleler Geraden immer den gleichen Abstand voneinander und außerdem haben zwei parallele Geraden keine gemeinsamen Punkte.

Beispielsweise sind die folgenden zwei Linien parallel:

Wir geben im Allgemeinen an, dass zwei Geraden parallel sind, mit zwei vertikalen Balken || zwischen den Zeilen

Andererseits sagen wir in der analytischen Geometrie, dass sie trotz der Tatsache, dass sich zwei parallele Linien nie schneiden, einen Winkel von 0° bilden, da sie die gleiche Richtung haben.

Wann sind zwei Geraden parallel?

Sobald wir die Definition paralleler Geraden kennengelernt haben, werden wir sehen, wie man zwei parallele Geraden findet. Natürlich wäre eine Möglichkeit, die Linien grafisch darzustellen und zu sehen, ob sie sich im Diagramm schneiden, aber es gibt noch einfachere und benutzerfreundlichere Methoden.

Bestimmen Sie die Parallelität zweier Geraden anhand ihrer Steigungen

Sie können erkennen, ob zwei Geraden parallel sind, indem Sie sich die Steigung jeder Geraden ansehen. Denken Sie daran, dass die Steigung einer Geraden der Parameter ist

$m$

aus der expliziten Gleichung und der Punkt-Steigungsgleichung der Geraden:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Es gibt jedoch mehrere Möglichkeiten, die Steigung einer Geraden zu bestimmen. Um herauszufinden, wie man sie berechnet, empfehlen wir einen Blick auf die Formel für die Steigung einer Geraden . Zusätzlich finden Sie auf der verlinkten Seite auch eine Erklärung, was die Steigung einer Geraden ausmacht und warum sie für eine Gerade so wichtig ist.

In der Ebene sind also zwei Geraden parallel, wenn sie die gleiche Steigung (Koeffizient m) und unterschiedliche Ordinaten im Ursprung (Koeffizient n) haben .

Beispielsweise sind die folgenden zwei Linien parallel:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

Es handelt sich um zwei parallele Geraden, weil beide die gleiche Steigung haben und außerdem ihre unabhängigen Terme unterschiedlich sind.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

Es ist zu beachten, dass zwei Linien identische Linien wären, wenn sie die gleiche Steigung und gleichzeitig denselben Computer im Ursprung hätten, weil sie genau identisch wären.

Finden Sie die Parallelität zweier Geraden aus der impliziten Gleichung

Denken Sie daran, dass die implizite (oder allgemeine) Gleichung der Geraden lautet:

$Ax+By+C=0$

Wenn also die Koeffizienten A und B zweier Geraden zueinander proportional sind, nicht jedoch zum Koeffizienten C , bedeutet dies, dass die Geraden parallel sind.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

Hier sind zwei parallele Geraden, ausgedrückt in allgemeiner (oder impliziter) Gleichungsform:

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

Sie sind parallel, weil die Zahlen vor der Variablen stehen

$x$

sind proportional zu den Zahlen vor der Variablen

$y$

, jedoch nicht mit unabhängigen Begriffen.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

Wenn wie zuvor alle Koeffizienten (A, B und C) zweier impliziter Linien proportional wären, würde dies bedeuten, dass die beiden Linien übereinstimmen, oder mit anderen Worten, dass sie gleich sind.

Eigenschaften paralleler Linien

Die Eigenschaften paralleler Linien sind wie folgt:

Symmetrische Eigenschaft : Wenn eine Linie parallel zu einer anderen ist, ist diese Linie auch parallel zur ersten. Diese Eigenschaft besitzen auch senkrechte Linien.

$r \parallel s \ \longrightarrow \ s \parallel r$

Transitive Eigenschaft : Wenn eine Linie parallel zu einer anderen Linie ist und diese zweite Linie parallel zu einer dritten Linie ist, ist die erste Linie auch parallel zur dritten Linie.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

Das Skalarprodukt der Richtungsvektoren (Vektor, der die Richtung einer Geraden angibt) zweier paralleler Geraden ist gleich dem Produkt ihrer Module.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

Darüber hinaus sind die Richtungsvektoren zweier paralleler Geraden stets linear voneinander abhängig, da sie proportional sind.

Diese Bedingung ist notwendig, damit Linien parallel sind, aber nicht ausreichend, oder mit anderen Worten, zwei parallele Linien müssen proportionale Richtungsvektoren haben, aber die Tatsache, dass zwei Linien proportionale Richtungsvektoren haben, bedeutet nicht direkt, dass sie parallel sind. Da zusammenfallende Linien auch proportionale Richtungsvektoren haben.

Linien parallel zur Abszissenachse (X-Achse) sind horizontal und haben immer die Form
$y=k.$

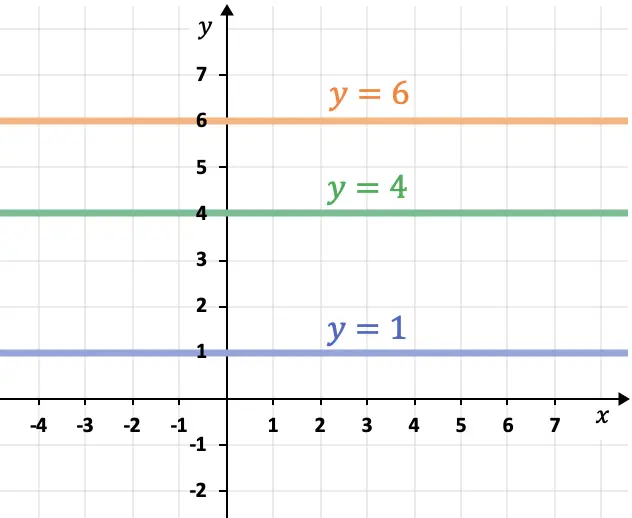
Linien parallel zur Computerachse (Y-Achse) sind vertikal und folgen immer dem Ausdruck
$x=k.$

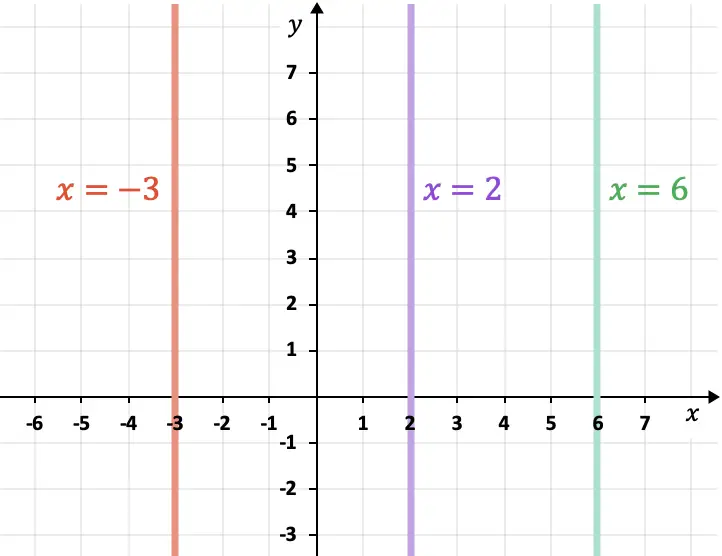
So berechnen Sie den Abstand zwischen zwei parallelen Linien in der Ebene

Um den Abstand zwischen zwei parallelen Geraden in der Ebene (in R2) zu ermitteln, nehmen Sie einfach einen Punkt auf einer der beiden Geraden und berechnen Sie den Abstand von diesem Punkt zur anderen Geraden.

Wir können es so machen, weil zwei parallele Linien immer den gleichen Abstand voneinander haben.

Wenn wir andererseits bei Verwendung der Formel einen Abstand von 0 Einheiten erhalten, bedeutet dies, dass sich die Linien an einem bestimmten Punkt berühren und daher nicht parallel sind, sondern sich schneiden, zusammenfallen oder senkrecht stehen. Wenn Sie möchten, können Sie die Unterschiede zwischen dieser Art von Leitungen auf unserer Website überprüfen.

Damit Sie sehen können, wie das geht, ermitteln wir beispielhaft den Abstand zwischen den folgenden zwei parallelen Geraden:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Als Erstes müssen wir einen Punkt auf einer der Linien (der gewünschten) erreichen. In diesem Fall berechnen wir einen Punkt auf der Linie

$s.$

Dazu müssen wir einer der Variablen einen Wert zuweisen, was wir zum Beispiel tun werden

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Und jetzt löschen wir die andere Variable (

$y$

) der erhaltenen Gleichung, um zu wissen, wie viel sie zu diesem Zeitpunkt wert ist:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Daher wird der Punkt aus der Linie erhalten

$s$

Ost:

$P(0,-2)$

Und sobald wir bereits einen Punkt auf einer Linie haben, berechnen wir den Abstand von diesem Punkt zur anderen Linie mithilfe der Formel für den Abstand von einem Punkt zu einer Linie:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

Der Abstand zwischen den beiden parallelen Geraden beträgt also 0,45 Einheiten .

Parallele Linien lösten Probleme

Übung 1

Welche der folgenden Geraden sind parallel?

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

siehe Lösung

Zwei Geraden sind parallel, wenn sie die gleiche Steigung (und unterschiedliche Schnittpunkte) haben. Somit beträgt die Steigung jeder Geraden:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

Es sind also nur die Linien parallel

$r$

Und

$q,$

weil sie die einzigen sind, die gleiche Steigungen haben.

Übung 2

Finden Sie die explizite Gleichung der Geraden parallel zur Geraden

$r$

und was passiert über den Punkt hinweg

$P(0,2).$

gerade sein

$r:$

$r: \; y=3x-1$

siehe Lösung

Damit die Linie parallel zur Linie ist

$r,$

beide müssen die gleiche Steigung haben. und die Steigung der Linie

$r$

ist 3:

$m = 3$

Daher lautet die explizite Gleichung der Geraden, die wir finden müssen:

$y=3x+n$

Und sobald wir die Steigung der Geraden kennen, können wir den Achsenabschnitt berechnen, indem wir den Punkt, der zur Geraden gehört, in die Geradengleichung einsetzen:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

Die explizite Gleichung der Geraden lautet also:

$\bm{y=3x+2}$

Übung 3

Berechnen Sie den Wert der Unbekannten

$a$

Und

$b$

sodass die folgenden beiden Geraden parallel sind:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

siehe Lösung

Die Linien werden in allgemeiner (oder impliziter) Gleichungsform beschrieben. Damit die beiden Geraden parallel sind, müssen ihre Koeffizienten A und B proportional sein, d. h. die folgende Gleichung muss erfüllt sein:

$\cfrac{2}{1} = \cfrac{-4}{a}$