Brüche oder gemischte Zahlen sind numerische Ausdrücke, die eine durch eine andere geteilte Größe angeben. Es handelt sich also um einen Wert, der durch den Quotienten zweier Zahlen dargestellt wird. Mit dieser Art von Zahlen können wir dezimale und ganzzahlige Größen ausdrücken und sogar Proportionen angeben. Als Nächstes definieren wir Brüche auf eine mathematischere Art und Weise und zeigen Ihnen einige Beispiele, damit Sie dieses Konzept anschaulich verstehen.
Was sind Brüche?
Ein Bruch ist gleich der Anzahl der Teile, die wir aus einer in gleiche Teile geteilten Einheit entnehmen. Grafisch wird es also durch zwei Begriffe dargestellt, die durch eine horizontale Linie in der Mitte getrennt sind . Genauer gesagt finden wir oben in der Zeile den Zähler und darunter den Nenner.
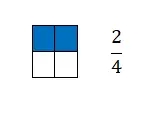
Wie Sie sehen, sind Brüche ein sehr einfach darzustellendes mathematisches Konzept, da sie mit Proportionen einhergehen. Aus diesem Grund haben wir im vorherigen Beispiel die Anzahl der farbigen Quadrate mit einer Bruchzahl ausgedrückt.
Bruchbegriffe
Die zwei Teile des Bruchs sind:
- Zähler: Dieser Begriff befindet sich über der horizontalen Linie und hier schreiben wir die Anzahl der Stücke, die wir nehmen. Wir können positive, negative und Null-Zähler (gleich Null) finden.
- Nenner: Dieser andere Begriff befindet sich unterhalb der Linie und hier schreiben wir die Gesamtzahl der Teile, in die die Einheit unterteilt ist. Wir können positive und negative Nenner finden, aber diese können nicht Null sein.
Arten von Brüchen
Es gibt viele Arten von Brüchen, abhängig von den Zahlen, aus denen sie bestehen, und der Äquivalenz, die sie mit anderen Brüchen aufweisen. Als nächstes definieren wir alle vorhandenen Kategorien und kommentieren die Merkmale, die es ermöglichen, sie von den anderen zu unterscheiden:
- Echte Brüche: sind Brüche, deren Zähler kleiner als der Nenner ist. Wenn Sie diese Brüche in eine Dezimalzahl umwandeln, erhalten Sie eine Zahl zwischen Null und Eins. Er kann nicht größer als eins sein, da der Wert des Zählers immer kleiner als der des Nenners sein wird und daher die Einheit nicht überschritten wird.
- Unechte Brüche: sind solche, deren Zähler größer als der Nenner ist. In diesem Fall drücken sie numerische Werte größer als eins aus. Beispielsweise ist 8/5 gleich 1,6, was größer als 1 ist. Dies ist eine weitere Möglichkeit, gemischte Zahlen auszudrücken, die vom folgenden Typ sind.
- Gemischte Brüche: auch gemischte Zahlen genannt, sind solche, die aus einer ganzen Zahl und einer gemischten Zahl bestehen. Grundsätzlich werden sie mit dem ganzzahligen Wert vor dem Bruch dargestellt. Um sie also in unechte Brüche umzuwandeln, müssen Sie den ganzzahligen Teil mit dem Nenner multiplizieren, ihn zum Zähler addieren und den Nenner gleich lassen.
- Dezimalbrüche: sind solche, deren Nenner eine Zahl ausdrückt, die einer Zehnerpotenz entspricht, zum Beispiel: 6/10, 34/1000 oder 5/100. Diese werden in der Dezimalschreibweise verwendet und kommen am häufigsten bei der Konvertierung exakter Dezimalzahlen in gemischte Zahlen vor. Wir werden dies im nächsten Abschnitt ausführlicher besprechen.
- Zusammengesetzte Brüche: sind solche, die aus einem anderen Bruch bestehen, entweder im Zähler, im Nenner oder in beiden. Um diese Ausdrücke zu vereinfachen und sie als einzelnen Bruch darzustellen, müssen wir den Zähler durch den Nenner dividieren. Dies wird klarer, wenn wir die Aufteilung zwischen Brüchen erklären.
- Äquivalente Brüche: sind solche, die derselben Zahl entsprechen, obwohl sie nicht aus denselben Zählern oder Nennern bestehen. Zum Beispiel 8/4 = 4/2 = 2, beide Brüche sind gleich zwei. In diesem speziellen Fall liegt es daran, dass der erste Bruch gleich dem Doppelten des zweiten ist und daher eine proportionale Beziehung besteht.
- Irreduzible Brüche: Dies sind Brüche, die nicht weiter vereinfacht werden können, da Zähler und Nenner keine gemeinsamen Faktoren haben und daher nicht durch eine beliebige Zahl dividiert werden können. Einige Beispiele dieser Art sind unter anderem: 9/5, 5/6, 7/8. Um sie zu erkennen, ist es wichtig zu wissen , wie man den größten gemeinsamen Teiler berechnet .
Operationen mit Brüchen
Nachdem wir nun die verschiedenen Kategorien von Brüchen kennen, die es gibt, werden wir sehen, wie man die verschiedenen arithmetischen Operationen mit gemischten Zahlen löst. Es ist zu beachten, dass dies etwas komplizierter ist als Operationen mit ganzen Zahlen, obwohl, sobald man die Methodik verstanden hat, alles recht einfach ist. Darüber hinaus erklären wir Ihnen nicht nur die Theorie, sondern zeigen Ihnen auch einige Beispiele. Nachdem dies gesagt ist, fangen wir an.
Summe der Brüche
Brüche mit einem gemeinsamen Nenner zu addieren ist ganz einfach, da man einfach die beiden Zähler addiert und den Nenner gleich lässt. Andererseits wird das Addieren von Brüchen mit unterschiedlichen Nennern etwas knifflig, da man das kleinste gemeinsame Vielfache der Nenner ermitteln muss. Und dann müssen wir das Produkt jedes Zählers addieren, indem wir den lcm (den neuen Nenner) durch den alten Nenner dividieren. Zum besseren Verständnis können Sie sich das folgende Diagramm ansehen:
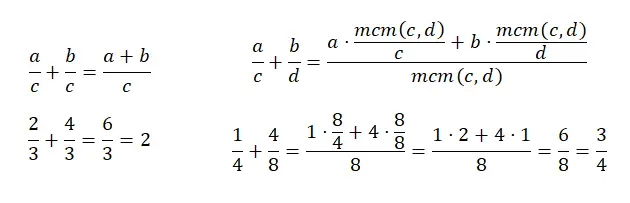
Subtraktionsbrüche
Die Subtraktion von Brüchen mit einem gemeinsamen Nenner ist der Addition sehr ähnlich, tatsächlich wird alles auf die gleiche Weise durchgeführt, außer bei der Summe der Zähler, denn statt zu addieren, muss man subtrahieren. Und bei der Subtraktion von Brüchen mit unterschiedlichen Nennern passiert dasselbe, es ist praktisch dasselbe, außer dass wir, anstatt das Produkt der Zähler zu addieren, indem wir den lcm durch den alten Nenner dividieren, subtrahieren müssen. Hier ist ein weiteres Diagramm:
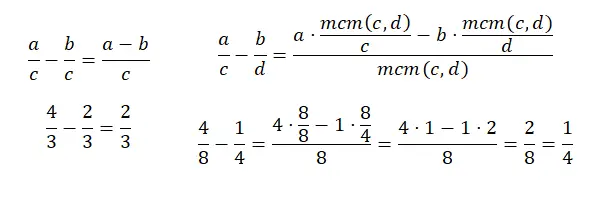
Multiplikation von Brüchen
Die Multiplikation von Brüchen kann auf die gleiche Weise gelöst werden, unabhängig davon, ob die Nenner gleich sind oder nicht. Grundsätzlich müssen Sie die Zähler mit einem Teil und die Nenner mit einem anderen multiplizieren. Dies ist vielleicht die einfachste Operation, da Sie nur zwei Multiplikationen durchführen müssen.
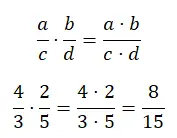
Division von Brüchen
Auch die Division in Brüche ist recht einfach zu lösen, man muss lediglich die Kreuze multiplizieren. Mit anderen Worten: Der Zähler ist das Ergebnis der Multiplikation des Zählers des ersten Bruchs mit dem Nenner des zweiten. wohingegen der Nenner das Produkt des Nenners des ersten Bruchs und des Zählers des zweiten ist.
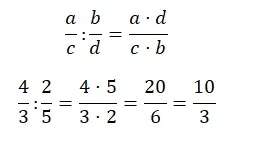
Brüche vereinfachen
Das Vereinfachen von Brüchen oder das Reduzieren von Brüchen ist keine arithmetische Operation als solche, aber es ist sehr wichtig zu wissen, wie man es macht, und außerdem ist es ein Thema, das wir bereits ein wenig mit den Arten von Brüchen behandelt haben. Um also eine gemischte Zahl zu vereinfachen, müssen wir Zähler und Nenner durch dieselbe Zahl dividieren. Im Allgemeinen wählen wir für diese Vereinfachung den größten gemeinsamen Faktor . Im folgenden Bild finden Sie ein Beispiel.
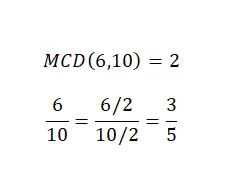
Wie Sie sehen, haben wir zwei äquivalente Brüche , also stellen beide denselben numerischen Wert dar, aber der zweite ist einfacher als der erste. Damit haben wir das Vereinfachungsziel erfolgreich erreicht.
Wie kommt man von Dezimalzahl zu Bruchzahl und umgekehrt?
Der erzeugende Bruch ist der irreduzible Bruch, der aus einer Dezimalzahl erhalten wird, entweder einer exakten Dezimalzahl oder einer sich wiederholenden Dezimalzahl. Natürlich müssen wir je nach Dezimaltyp unterschiedliche Methoden verwenden, die wir weiter unten besprechen werden.
Konvertieren Sie von einer exakten Dezimalzahl in einen erzeugenden Bruch
In diesem Fall können wir auf die Dezimalbrüche zurückgreifen, die wir eingangs kommentiert haben. Wir müssen einfach den numerischen Wert im Zähler schreiben, jedoch ohne Dezimalpunkt. Im Nenner schreiben wir die Zehnerpotenz, die so viele Nullen hat, wie Ziffern im Zähler sind.
Wenn wir jedoch eine Dezimalzahl haben, die größer als eins ist, beispielsweise 4,25, müssen wir die Anzahl der vollständigen Einheiten, die wir haben, mit dem Nennerwert multiplizieren und ihn zum ursprünglichen Zähler addieren. Nachfolgend finden Sie ein Beispiel für jeden Typ:
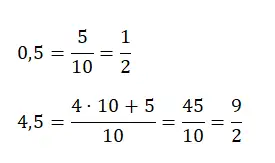
Konvertieren Sie eine reine sich wiederholende Dezimalzahl in einen erzeugenden Bruch
Wenn wir eine reine periodische Dezimalzahl haben und den erzeugenden Bruch erhalten möchten, müssen wir denselben Wert in den Zähler eingeben, jedoch ohne Dezimalpunkt, und den ganzzahligen Teil subtrahieren. Während der Nenner einer Zahl entspricht, die nur aus Neunen besteht, müssen wir genau so viele Neunen schreiben, wie es Ziffern im Dezimalteil der ursprünglichen Zahl gibt. Dieses System ist etwas verwirrend, aber anhand einiger Beispiele werden wir es verstehen:
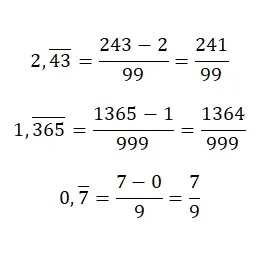
Wandeln Sie gemischte wiederholte Dezimalzahlen in Brüche um
Im Falle einer gemischten wiederholten Dezimalzahl müssen wir eine ziemlich komplexe Regel anwenden. Zuerst schreiben wir die Zahl ohne Komma im Zähler und subtrahieren den ganzzahligen Teil, gefolgt von den einmaligen Dezimalstellen, ebenfalls ohne Komma. Was den Nenner betrifft, müssen Sie so viele Neunen schreiben, wie Ziffern im periodischen Dezimalteil vorhanden sind, gefolgt von so vielen Nullen, wie Ziffern im nicht wiederkehrenden Dezimalteil vorhanden sind.
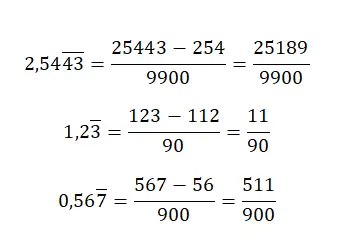
Bruch in Dezimalzahl umwandeln
Um von einem Bruch zu einer Dezimalzahl zu gelangen, dividieren Sie einfach den Zähler durch den Nenner, denn eine gemischte Zahl ist nichts anderes als der Quotient zwischen zwei Werten . Wenn Sie also die Division lösen, erhalten Sie die entsprechende Dezimalzahl. Im folgenden Bild finden Sie einige recht einfache Beispiele:
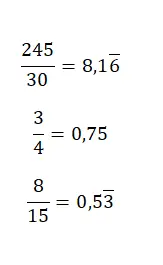
Übungen zu Brüchen
Nachdem Sie nun die gesamte Theorie über Brüche kennen, empfehlen wir Ihnen, einige Übungen zu machen. Auf diese Weise lernen Sie alle Konzepte ausführlicher und kommen am Tag der Prüfung schneller bei der Lösung der Berechnungen voran. Darüber hinaus haben Sie alle Arten von Bruchübungen gesehen, die es gibt, und wissen, wie Sie diese entsprechend lösen können. Abschließend möchte ich Ihnen sagen, dass wir Ihnen auch einen Online- Bruchrechner zur Verfügung stellen, mit dem Sie alle Bruchrechnungen lösen können.