Auf dieser Seite finden Sie die Erklärung, was Newtons Binomial (oder Binomialsatz) ist und wie seine Formel lautet. Sie können auch sehen, wie dies mit dem Tartaglia- (oder Pascal-) Dreieck vereinfacht werden kann. Darüber hinaus finden Sie Schritt für Schritt gelöste Übungen zum Newtonschen Binomial und all seinen Eigenschaften. Abschließend erklären wir die Kuriositäten hinter dem Ursprung dieses ganz besonderen Theorems.
Was ist Newtons Binomial?
In der Mathematik ist das Newtonsche Binomial , auch Binomialsatz genannt, eine Formel, mit der Sie die Potenz eines Binomials einfach berechnen können. Mit anderen Worten besteht das Newtonsche Binomial aus einer Formel, mit der algebraische Ausdrücke der Form (a+b) gelöst werden können.
Offensichtlich ist dieser Satz nach dem Physiker, Mathematiker und Philosophen Sir Isaac Newton benannt. Diesbezüglich gibt es jedoch einige Kontroversen, da Texte aus dem Nahen Osten gefunden wurden, in denen dieser Satz bereits verwendet wurde. Im Folgenden werden wir ausführlich auf den Ursprung dieser mathematischen Formel eingehen.
Newtons Binomialformel
Wie wir in der Definition des Newtonschen Binomials gesehen haben, wird dieser Satz verwendet, um die Potenzen von Binomialen zu lösen. Aber… wie wird Newtons Binomial angewendet? Oder anders ausgedrückt: Wie lautet Newtons Binomialformel?
Die mathematische Formel für das Newtonsche Binomial lautet wie folgt:
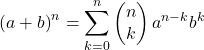
Oder gleichwertig:
![]()
Die Formel ist etwas komplex, um das Konzept des Newtonschen Binomials zu verstehen. Deshalb haben wir im Folgenden die Potenzen von Binomialen des niedrigsten Grades dargestellt, damit Sie sie besser verstehen können:

Wie Sie sehen können, nehmen beim Erweitern eines Binomials die Exponenten des ersten Termes (a) ab, während die Exponenten des zweiten Termes (b) zunehmen , genau wie das untere Element kombinatorischer Zahlen zunimmt.
Um den Binomialsatz anwenden zu können, müssen Sie daher wissen, wie eine kombinatorische Zahl, also der algebraische Ausdruck des Typs, gelöst wird
![]()
. Bevor wir uns also Beispiele für die Berechnung eines Newton-Binoms ansehen, werfen wir einen kurzen Blick auf kombinatorische Zahlen.
kombinatorische Zahl
Um eine kombinatorische Zahl (oder einen Binomialkoeffizienten) zu bestimmen, müssen Sie die folgende Formel anwenden:
![]()
Gold
![]()
Und
![]()
Das sind Fakultätszahlen . Erinnern wir uns auch daran, dass eine Fakultätszahl berechnet wird, indem alle positiven ganzen Zahlen von 1 mit dieser Zahl multipliziert werden:
![]()
Als Beispiel finden wir eine kombinatorische Zahl, damit Sie sehen können, wie es gemacht wird:
![]()
Kombinatorische Zahlen können auch über den Taschenrechner mit der Taste ermittelt werden
![]()
Beispiele für Newton-Binomiale
Nachdem wir nun wissen, was der Binomialsatz ist, sehen wir uns anhand zweier numerischer Beispiele an, wie man Newtons Binomialformel anwendet.
Beispiel 1
- Wenden Sie Newtons Binomial an, um die Potenz des folgenden Binomials zu berechnen:
![]()
Da dieses Binomial quadriert ist, könnte es natürlich auch mit den Formeln für bemerkenswerte Identitäten gelöst werden ( wie man bemerkenswerte Identitäten löst ), aber wir werden es anhand des Binomialsatzes als Beispiel berechnen.
Zunächst müssen wir die Binomialformel von Newton anwenden:
![]()
In diesem Fall ist n=2, also:
![]()
Schauen Sie genau hin, am Anfang erhöhen wir den ersten Term (x) auf den maximal möglichen Wert, der in diesem Fall 2 ist. Andererseits erhöhen wir den zweiten Term (3) auf den minimal möglichen Wert, der immer 0 ist. Aber Wenn wir nach rechts gehen, müssen wir den ersten Term auf eine niedrigere Zahl als zuvor und den zweiten Term auf eine höhere Zahl als zuvor erhöhen.
Berechnen wir nun die kombinatorischen Zahlen:
![]()
Wir lösen nach den Potenzen auf:
![]()
Und schließlich berechnen wir die Multiplikationen:
![]()
Beispiel 2
Jetzt werden wir ein etwas schwierigeres Problem lösen.
- Wenden Sie die Binomialformel von Newton an, um die Potenz des folgenden Binomials zu ermitteln:
![]()
Die Formel für den Binomialsatz lautet:
![]()
In diesem Fall ist n=3, also:
![]()
Wir berechnen die kombinatorischen Zahlen:
![]()
Nun lösen wir die Potenzen, hierfür ist es wichtig, dass Sie sich die folgenden zwei Eigenschaften merken:
• Wenn ein Monom auf einen Exponenten erhöht wird, werden der Koeffizient und die Variable auf denselben Exponenten erhöht →
![]()
• Jeder Term, der auf 0 gebracht wird, ergibt 1 →
![]()
Wir finden die Kräfte daher durch diese 2 Eigenschaften:
![]()
![]()
Und schließlich multiplizieren wir die Terme:
![]()
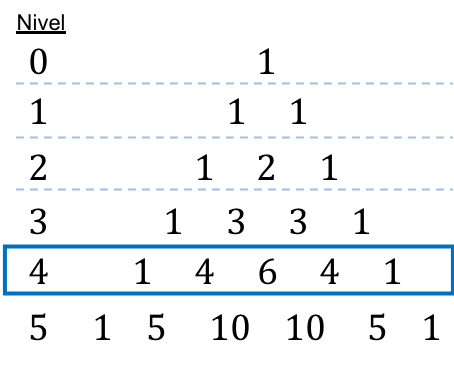
Newtons Binomial und Tartaglias (oder Pascals) Dreieck
Wie Sie in den obigen Beispielen gesehen haben, ist die Berechnung kombinatorischer Zahlen etwas mühsam. Deshalb bringen wir Ihnen einen Trick bei, damit Sie kombinatorische Zahlen nicht lösen müssen, da Sie mithilfe des Tartaglia-Dreiecks, auch bekannt als Pascal-Dreieck, direkt herausfinden können, wie viel sie wert sind.
Falls Sie nicht wissen, was es ist: Das Tartaglia-Dreieck , auch Pascal-Dreieck genannt, ist eine mathematische Darstellung von Zahlen, die in Dreiecksform angeordnet sind.
Um das Tartaglia- oder Pascal-Dreieck zu konstruieren, müssen wir am Scheitelpunkt des Dreiecks beginnen, der immer eine 1 ist, und dann die Nummern der darunter liegenden Linien bestimmen. Jede Zahl in den folgenden Zeilen ist gleich der Summe der beiden Zahlen direkt darüber, mit Ausnahme der Enden der Zeilen, die immer 1 sind.
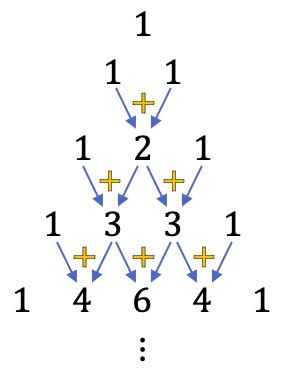
Jede dieser Zahlen im Tartaglia-Dreieck entspricht also dem Ergebnis einer kombinatorischen Zahl, siehe folgende Abbildung:
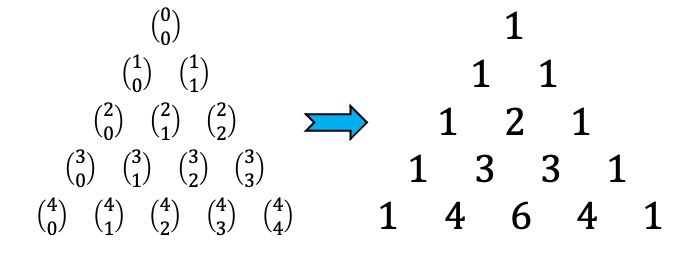
Zum Beispiel der Binomialkoeffizient
![]()
entspricht 3, da im Tartaglia-Dreieck an seiner Position eine 3 steht.
Wir können daher das Dreieck von Tartaglia (oder Pascal) verwenden, um das Newtonsche Binomial viel schneller zu lösen, da es uns die Berechnung kombinatorischer Zahlen erspart.
Wenn wir beispielsweise die folgende Potenzierung eines Binomials durchführen möchten:
![]()
Durch Anwendung der Newtonschen Binomialregel erhalten wir den folgenden algebraischen Ausdruck:
![]()
Anstatt die kombinatorischen Zahlen einzeln zu berechnen, können wir einfach jede kombinatorische Zahl durch den entsprechenden Koeffizienten des Tartaglia-Dreiecks ersetzen. In diesem Fall wird das Binomial auf die 3. angehoben, es entspricht also der dritten Ebene des Dreiecks:
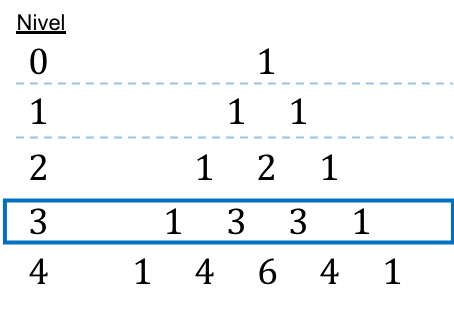
![]()
Und jetzt müssen wir nur noch die restlichen Operationen durchführen:
![]()
![]()
Wie Sie sehen können, wird das Dreieck von Tartaglia (oder Pascal) verwendet, um das Newtonsche Binomial auf einfachere und schnellere Weise zu berechnen, wie wir gezeigt haben. Aus diesem Grund empfehlen wir die Verwendung.
Um alles, was wir bisher gesehen haben, zusammenzufassen, hinterlassen wir Ihnen ein Bild, das zeigt, wie die Ausdrücke der Newtonschen Binomiale mit den Zahlen des Tartaglia- (oder Pascal-) Dreiecks aussehen:

Negatives Newton-Binom: Subtraktionskraft
Bisher waren alle Beispiele des Newtonschen Binomials, die wir gelöst haben, Ergänzungen. Wenn andererseits einer der beiden Terme des Binomials ein negatives Vorzeichen hat, bleibt das Verfahren ähnlich, ändert sich jedoch ein wenig.
Wenn einer der Terme des Binomials negativ ist, also eine Subtraktion vom Typ (ab) n ist, müssen sich die Vorzeichen der Entwicklung des Newton-Binoms in der Form + – + – + – + – … abwechseln.
Nachfolgend haben wir die Potenzen der negativen Binome der ersten 5 Grade mit dem Binomialsatz und den bereits vorhandenen Koeffizienten des Tartaglia-Dreiecks entwickelt, damit Sie direkt den benötigten Binomialausdruck finden können:

Eigenschaften des Newtonschen Binomials
Newtons Binomialausdrücke weisen die folgenden Merkmale auf:
- Die Zerlegung des Newtonschen Binomials ergibt immer einen Term mehr als den Grad des Binomials. Oder anders ausgedrückt: für das Paar
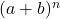
sie sind betroffen
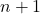
Bedingungen.
- Die Kräfte des Elements

Beginnen mit
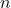
und sie nehmen ab, bis sie im letzten Quartal 0 erreichen.
- Die Kräfte des Elements
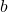
Sie gehen in die andere Richtung: Sie beginnen bei 0 und steigern sich, bis sie den Wert erreichen
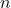
im letzten Semester.
- Für jedes Element des Newtonschen Binomials ist die Summe der Exponenten von

Und
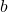
ist gleich
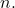
- Der Koeffizient des ersten Termes des Newtonschen Binomialausdrucks ist immer 1 (positiv) und der zweite Koeffizient entspricht dem Exponenten des Binomialausdrucks (positiv oder negativ).
Berechnen Sie den k-ten Term des Newtonschen Binomials
Obwohl dies ungewöhnlich ist, können wir manchmal auf Probleme stoßen, bei denen wir anstelle der Newtonschen Binomialentwicklung aufgefordert werden, den k-ten Term des Newtonschen Binomials zu bestimmen, d. h. den Term, der die Position k einnimmt.
Um also den Term zu berechnen, der die Stelle k im Newtonschen Binomial einnimmt, müssen wir eine Formel verwenden, die davon abhängt, ob das Binomial eine Addition oder eine Subtraktion ist:
- Wenn das Newtonsche Binomial positiv ist, wird der Wert des k-ten Termes mit der folgenden Formel berechnet:
![]()
- Wenn das Newtonsche Binomial negativ ist, wird der Wert des k-ten Termes mit der folgenden Formel bestimmt:
![]()
Als Beispiel finden wir den vierten Term des folgenden Binomials 5. Grades:
![]()
Da es sich um ein aus einer Summe zusammengesetztes Binomial handelt, wenden wir die erste Formel an:
![]()
Wir ersetzen die Variablen in der Formel durch ihre entsprechenden Werte:
![]()
Und wir führen die Operationen durch:
![]()
![]()
![]()
Und auf diese Weise haben wir den vierten Term der Newtonschen Binomialentwicklung berechnet, ohne alle anderen Terme berechnen zu müssen.
Gelöste Übungen zum Newtonschen Binomial
Nachdem wir nun erklärt haben, was der Binomialsatz ist, überlassen wir Ihnen einige gelöste Schritt-für-Schritt-Übungen zum Newtonschen Binomialsatz, damit Sie üben können. Denken Sie auch daran, dass Sie uns in den Kommentaren Fragen oder Anregungen hinterlassen können.
Übung 1
Erweitern Sie die folgende Binomialpotenz mithilfe des Binomialsatzes:
![]()
Wir verwenden zunächst Newtons Binomialformel:
![]()
Da das Binomial auf die Potenz 3 erhöht wird, schauen wir uns die dritte Ebene des Tartaglia-Dreiecks an, um die kombinatorischen Zahlen direkt zu finden:

![]()
Wir führen die Befugnisse aus:
![]()
Und schließlich multiplizieren wir:
![]()
![]()
Übung 2
Berechnen Sie die folgende Potenz mit der Newtonschen Binomialformel:
![]()
Zunächst wenden wir Newtons Binomialformel an:
![]()
Da das Binomial kubisch ist, schauen wir uns die dritte Ebene des Pascalschen Dreiecks an, um die Werte der kombinatorischen Zahlen direkt zu kennen:

![]()
Wir berechnen die Potenzen der Monome:
![]()
Und schließlich führen wir die Multiplikationen durch:
![]()
![]()
Übung 3
Erweitern Sie den folgenden Polynomausdruck mithilfe der Newtonschen Binomialformel:
![]()
Zunächst verwenden wir die Binomialformel von Newton. Da wir aber in den Klammern eine Subtraktion haben, müssen wir die Vorzeichen der Koeffizienten jedes Termes wechseln:
![]()
Da das Binomial mit drei potenziert wird, schauen wir uns die dritte Ebene des Tartaglia-Dreiecks an, um die kombinatorischen Zahlen direkt zu berechnen:

![]()
Wir führen die Befugnisse aus:
![]()
Und wir lösen die Multiplikationen:
![]()
![]()
Übung 4
Finden Sie den erweiterten Ausdruck des folgenden Newton-Binoms mit der Formel:
![]()
Wir müssen die allgemeine Formel für das Newtonsche Binomial anwenden, aber da wir in diesem Fall eine Subtraktion in Klammern haben, müssen wir die Vorzeichen jedes Termes wechseln:
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7a8620bd23846e1f98f7646cbd51dbc5_l3.png)
Da das Binomial auf die vierte angehoben wird, schauen wir uns die Ebene 4 des Tartaglia-Dreiecks an, um die kombinatorischen Zahlen direkt zu finden:
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-128e8baa45ddd7d74703c9dfd4a19b06_l3.png)
Wir erkennen alle Kräfte:
![]()
Und schließlich lösen wir die Multiplikationen:
![]()
![]()
Übung 5
Bestimmen Sie den siebten Term in der Entwicklung des folgenden Binomialausdrucks:
![]()
Da es sich um ein negatives Binomial handelt, müssen wir die folgende Formel verwenden:
![]()
Wir wollen den Term 7 bestimmen und das Binomial mit 10 potenzieren, sodass durch Einsetzen der Werte in die Formel Folgendes entsteht:
![]()
Es reicht daher aus, den Begriff zu kennen:
![Rendered by QuickLaTeX.com \begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ded0622cbba2bff0563c2f9982c05142_l3.png)
Geschichte des Newtonschen Binomials
Obwohl der Ursprung des Binomialsatzes dem berühmten englischen Wissenschaftler Isaac Newton (1642-1727) zugeschrieben wird, wurde die erste Formulierung des Satzes in Wirklichkeit erstmals um das Jahr 1000 vom persischen Ingenieur Al-Karijí entdeckt. Und das wurde sogar entdeckt Bereits im 13. Jahrhundert kannten die chinesischen Mathematiker Yang Hui und Chuh Shih-Chieh Binomialentwicklungen kleiner Grade.
Später, im 17. Jahrhundert, baute Newton auf den von früheren Mathematikern gelegten Grundlagen auf, um den Binomialsatz zu erweitern. Mithilfe der Interpolations- und Extrapolationsmethoden des Mathematikers John Walls und der Konzepte verallgemeinerter Exponenten gelang es ihm, einen Polynomausdruck in eine unendliche Reihe umzuwandeln.
Um 1665 gelang Newton der Nachweis, dass der Exponent n des Binomialsatzes auch ein rationaler Exponent sein könnte, das heißt, dass die Potenz eines Binomials auch dann gelöst werden kann, wenn der Exponent ein Bruch ist. Andererseits wurde es auch im Fall eines negativen Exponenten nachgewiesen. Und überraschenderweise entdeckte er, dass die Entwicklungen der beiden Ausdrücke eine unendliche Reihe von Begriffen sind.
Mit dieser Entdeckung begann Newton, die Beziehung zwischen unendlichen Reihen und endlichen Polynomausdrücken in Frage zu stellen und folgerte, dass mathematische Operationen mit unendlichen Reihen auf die gleiche Weise wie endliche Polynomausdrücke durchgeführt werden können. Obwohl Newton diesen Satz nie veröffentlichte, veröffentlichte John Walls dies schließlich im Jahr 1685 und schrieb Newton diese Entdeckung zu.