Binomiale – Mathematik

Auf dieser Seite finden Sie eine Erklärung, was ein Binomial ist, und außerdem können Sie Beispiele für jeden Binomialtyp sehen. Außerdem zeigen wir Ihnen die Formeln, die zur Lösung von Operationen mit Binomialen verwendet werden: Multiplikation von Binomialen, Binomialquadrat, Binomialkubik, …

Was ist ein Paar?

In der Algebra lautet die Definition eines Binomials:

Ein Binomial ist ein Polynom, das nur aus zwei Monomen besteht . Mit anderen Worten: Ein Binomial besteht aus einem algebraischen Ausdruck mit nur zwei verschiedenen Begriffen, die durch das Pluszeichen (+) oder das Minuszeichen (-) verbunden sind.

Das Wort Binomial stammt aus dem Griechischen und setzt sich aus zwei lexikalischen Bestandteilen ( bi und nomos ) zusammen, die Folgendes bedeuten:

bi : Präfixbedeutung 2.
nomos : bedeutet Teil.

Daraus können wir die Bedeutung des Binomials ableiten: Polynom mit zwei Teilen (oder 2 Monomen).

Andererseits hat der Begriff eines Paares eine andere Bedeutung als die mathematische, nämlich dass ein Paar auch eine Gruppe von zwei Persönlichkeiten bezeichnen kann, die im politischen Leben, in bestimmten Sportdisziplinen oder auch in der Unterhaltung eine führende Rolle spielen. . Aber natürlich konzentrieren wir uns hier auf die mathematische Definition des Binomials.

Beispiele für Binome

Um das Verständnis des Begriffs Binomial zu vervollständigen, sehen wir uns einige Beispiele dieser Art von Polynom an:

Beispiel für ein quadratisches Binomial:

$x^2+4x$

Beispiel für ein Binomial dritten Grades:

$x^3+5$

Beispiel für ein Binomial vierten Grades:

$3x^4+8x^2$

Nachdem wir nun wissen, was ein Binomial ist, werden wir die verschiedenen Arten von Binomialen sehen und sehen, wie Operationen mit Binomialen gelöst werden.

Binomialquadrat

Ein quadriertes Binomial ist eine bemerkenswerte Identität, die auch bemerkenswertes Produkt oder bemerkenswerte Gleichheit genannt wird. Das Auflösen nach der Potenz eines auf 2 erhöhten Binomials hängt davon ab, ob es sich um ein Summenbinomial oder ein Differenzbinomial handelt.

Ein Summenbinomial bezieht sich auf das Binomial, dessen zwei Terme positiv sind, das heißt, ein Quadratsummenbinomial ist:

$(a+b)^2$

Andererseits ist ein Differenz- (oder Subtraktions-)Binom das Konjugierte des Additions-Binoms, das heißt, eines seiner Monome hat ein negatives Vorzeichen. Daher lautet der algebraische Ausdruck für eine quadrierte Binomialdifferenz:

$(a-b)^2$

Um ein quadriertes Binomial zu berechnen, müssen Sie eine Formel anwenden, die, wie wir gesehen haben, je nachdem, ob es sich um eine Addition oder eine Subtraktion handelt, unterschiedlich ist. Wie das geht, erfahren Sie in den Formeln für bemerkenswerte Gleichheiten . Dort finden Sie alle Schritt-für-Schritt-Erklärungen sowie Beispiele und gelösten Aufgaben, und zwar nicht nur zu diesen beiden bemerkenswerten Gleichheiten, sondern zu allen.

Binomial gewürfelt

Obwohl sie seltener verwendet werden, gelten auch Würfelbinome als bemerkenswerte Produkte. Mit anderen Worten: Es gibt mathematische Regeln, die es Ihnen ermöglichen, schnell die Potenz eines Binomials zu finden (Sie können sie im obigen Link zu Formeln für bemerkenswerte Identitäten sehen).

Das Ergebnis dieser Potenzierung hängt wie zuvor davon ab, ob es sich um die Potenz einer Summe handelt:

$(a+b)^3$

Oder wenn die Potenz im Gegenteil durch die Potenz einer Differenz oder einer Subtraktion gebildet wird:

$(a-b)^3$

Logischerweise ist der Hauptunterschied zwischen einem quadrierten Binomial und einem kubischen Binomial der Potenzexponent. Allerdings ist die Formel für ein kubisches Binomial viel komplizierter als die für ein quadriertes Binomial.

bemerkenswerte Vereinbarungen

Es gibt insbesondere bestimmte Arten von Binomialen, die aufgrund ihrer Eigenschaften etwas speziell sind, da sie weniger bekannten bemerkenswerten Identitäten (oder bemerkenswerten Produkten) entsprechen.

Quadratsumme:
$a^2+b^2$
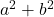
Differenz (oder Subtraktion) von Quadraten:
$a^2-b^2$
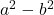
Summe der Würfel:
$a^3+b^3$
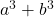
Differenz (oder Subtraktion) von Würfeln:
$a^3-b^3$

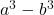
Gold

$a$

Und

$b$

sind zwei beliebige Monome.

Obwohl diese Binomialausdrücke denen, die wir gerade oben gesehen haben, sehr ähneln (Quadrat- und Kubikbinomial), unterscheiden sie sich bei genauem Hinsehen. In diesem Sinne können Sie auch die Formeln der bemerkenswerten Binome und ihre Ableitungen sehen, indem Sie auf den Link oben klicken ⬆ Formeln der bemerkenswerten Identitäten.⬆

Binomialmultiplikation

Eine der häufigsten Operationen mit Binomialen ist die Multiplikation. Als nächstes sehen wir uns ein Beispiel für die Berechnung einer Multiplikation zwischen Binomialen an.

$(x^2+2x)\cdot (x-5)$

Um die Binomialmultiplikation zu berechnen, müssen wir zunächst jeden Term im ersten Binomial mit jedem Term im zweiten Binomial multiplizieren:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

Als nächstes gruppieren wir ähnliche Begriffe, das heißt, sie haben den gleichen wörtlichen Teil:

$\bm{x^3-3x^2 -10x}$

Und auf diese Weise ist es uns gelungen, das Ergebnis des Produkts zwischen den Paaren zu finden.

Produkt zweier Binome mit einem gemeinsamen Term

Wenn die Binome, die an der Multiplikation teilnehmen, als gemeinsamen Term die Variable haben

$x,$

Es gibt eine Formel zur schnellen Berechnung dieser Binomialoperation:

$(x+a)(x+b) = x^2+(a+b)x+ab$

Hier zeigen wir Ihnen eine gelöste Übung, damit Sie sehen können, wie Sie diese Formel anwenden:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

Newtons Binomial

Newtons Binomialsatz , auch Binomialsatz genannt, ist eine Formel zur Berechnung der Potenzen von Binomialen.

Die mathematische Formel für das Newtonsche Binomial lautet wie folgt:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

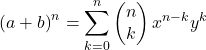
Oder gleichwertig:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Wie Sie sehen, ist diese Formel etwas komplex zu verstehen. Aus diesem Grund haben wir im Folgenden die Potenzen der Binome des niedrigsten Grades dargestellt, damit Sie es besser verstehen:

Diese Formel kann für die Berechnung von quadratischen oder kubischen Binomialen etwas mühsam sein, da es, wie wir oben gesehen haben, einfachere Formeln gibt. Das Newtonsche Binomial ist jedoch sehr nützlich, um Potenzen höheren Grades zu finden, beispielsweise wird es häufig zur Bestimmung eines Binoms zur Quarte verwendet.

Um diese Formel anwenden zu können, müssen Sie jedoch wissen, wie eine kombinatorische Zahl, also der algebraische Ausdruck des Typs, berechnet wird

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

, Berechnung nicht einfach. 🔍 Aus diesem Grund empfehlen wir Ihnen, in unserer Suchmaschine oben rechts zu suchen. 🔎 Dort finden Sie unseren Artikel, in dem wir Ihnen diesen Vorgang Schritt für Schritt erklären.