Berechnen sie den schnittpunkt bzw. schnittpunkt zweier geraden

Hier erfahren Sie, wie der Schnittpunkt (oder Schnittpunkt) zwischen zwei Linien berechnet wird. Sie sehen auch Beispiele und können mit Schritt für Schritt gelösten Übungen üben.

Was ist der Grenz- oder Schnittpunkt zwischen zwei Linien?

Der Schnittpunkt (oder Schnittpunkt) zwischen zwei Linien ist der Punkt, an dem sich zwei verschiedene Linien kreuzen. Wenn also zwei verschiedene Linien einen Schnitt- oder Schnittpunkt haben, bedeutet dies, dass sie in einem Punkt zusammenfallen.

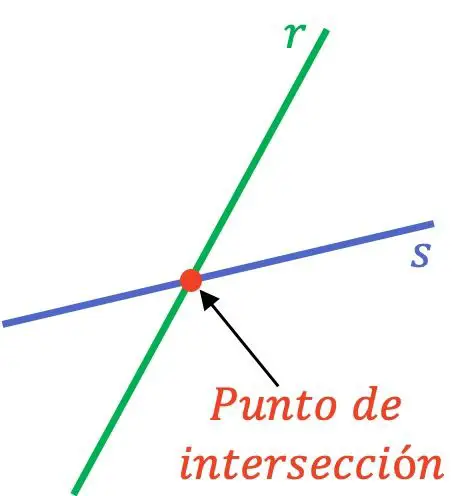
Damit sich zwei Geraden in einem Punkt schneiden, müssen sie sich schneidende Geraden sein, da sich parallele Geraden in keinem Punkt berühren.

Wenn Sie sich jetzt nicht mehr genau daran erinnern, was sich schneidende Linien sind, empfehlen wir Ihnen, einen Blick auf unsere Seite mit Beispielen für sich schneidende Linien zu werfen. Dort finden Sie eine ausführliche Erklärung, was diese Linientypen sind und wie Sie feststellen können, ob sich zwei Linien schneiden oder nicht.

Wie berechnet man den Grenz- oder Schnittpunkt zwischen zwei Linien?

Nachdem wir die Definition des Schnittpunkts oder Schnittpunkts zwischen zwei Linien gesehen haben, sehen wir uns nun an, wie dieser Punkt berechnet wird.

Um den Schnittpunkt (oder Schnittpunkt) zwischen zwei Geraden zu finden, müssen Sie zunächst sicherstellen, dass die beiden Geraden nicht parallel sind, denn wenn es sich um zwei parallele Geraden handelt, werden sie sich an keinem Punkt schneiden. Daher müssen Sie zunächst wissen, wie Sie feststellen können , wann zwei Geraden parallel sind und wann nicht. Wenn Sie sich nicht erinnern, wie es geht, können Sie es sich noch einmal ansehen, indem Sie auf den Link klicken.

Sobald wir wissen, dass die beiden Linien nicht parallel sind, müssen wir zur Bestimmung des Schnittpunkts (oder Schnittpunkts) zwischen den beiden Linien das Gleichungssystem lösen, das durch die Gleichung jeder Linie gebildet wird. Und das Ergebnis dieses Gleichungssystems sind die Koordinaten des Schnittpunkts (oder Schnittpunkts) zwischen den beiden Linien.

Beispiel, wie man den Schnittpunkt oder Schnittpunkt zweier Geraden findet

Als Beispiel lösen wir ein Problem, damit Sie sehen können, wie Sie den Schnittpunkt (oder Schnittpunkt) zwischen zwei Geraden finden:

• Finden Sie den Schnittpunkt zwischen den folgenden beiden Geraden:

Erstens sind die Linien nicht parallel, da sie unterschiedliche Steigungen haben, sodass sie sich beide in einem Punkt auf der kartesischen Ebene schneiden.

Um das herauszufinden, müssen wir das Gleichungssystem lösen, das aus der Gleichung jeder Geraden besteht:

In diesem speziellen Fall werden wir das System mit der Ausgleichsmethode lösen, da die beiden Unbekannten vorhanden sind

sind bereits gelöst (beide Zeilen liegen in expliziter Gleichungsform vor):

Wir löschen den Wert der Variablen

Und sobald Sie wissen, wie viel es wert ist

Wir setzen seinen Wert in eine beliebige Gleichung ein, um den Wert zu ermitteln

Damit sind die Koordinaten des Schnittpunkts der beiden Geraden:

Probleme mit Schnittpunkten oder Schnittpunkten zwischen zwei Linien gelöst

Übung 1

Was ist der Schnittpunkt bzw. Schnittpunkt zwischen den folgenden beiden Geraden?

Erstens sind die Linien nicht parallel, da sie unterschiedliche Steigungen haben, sodass sich die beiden Linien irgendwann in der Ebene treffen.

Um diesen Punkt zu berechnen, ist es notwendig, das Gleichungssystem zu lösen, das aus der Gleichung jeder Geraden besteht:

In diesem Fall lösen wir das Gleichungssystem mit der Ausgleichsmethode, da die beiden Unbekannten vorhanden sind

sind bereits gelöst (beide Zeilen liegen in expliziter Gleichungsform vor):

Wir löschen den Wert der Variablen

Und sobald Sie wissen, wie viel es wert ist

Wir setzen seinen Wert in eine beliebige Gleichung ein, um den Wert zu ermitteln

Die Koordinaten des Schnittpunkts der beiden Geraden lauten daher:

Übung 2

Finden Sie den Schnittpunkt bzw. Schnittpunkt zwischen den folgenden beiden Geraden:

das Recht

Sie wird in Form einer impliziten (oder allgemeinen) Gleichung ausgedrückt, daher übergeben wir sie zunächst in Form einer expliziten Gleichung, um den Wert ihrer Steigung zu kennen:

Die beiden Geraden haben also unterschiedliche Steigungen und daher gibt es einen Schnittpunkt zwischen ihnen.

Um diesen Punkt zu berechnen, ist es notwendig, das Gleichungssystem zu lösen, das aus der Gleichung jeder Geraden besteht:

Wir lösen das Gleichungssystem mit der Ausgleichsmethode:

Wir löschen den Wert der Variablen

Und sobald Sie wissen, wie viel es wert ist

Wir setzen seinen Wert in eine der beiden Gleichungen ein, um den Wert von zu ermitteln

Die Koordinaten des Schnittpunkts der beiden Geraden lauten daher:

Übung 3

Bestimmen Sie den Schnittpunkt bzw. Schnittpunkt zwischen den folgenden beiden Geraden:

Zunächst müssen wir wissen, ob es sich um zwei parallele Geraden handelt oder nicht. Dazu prüfen wir, ob die Richtungsvektoren der beiden Geraden proportional sind.

das Recht

ist in Form parametrischer Gleichungen definiert, daher sind die Komponenten seines Richtungsvektors die Koeffizienten vor dem Parameter

Und andererseits die Linie

wird in Form einer impliziten Gleichung beschrieben, daher ist sein Richtungsvektor:

Damit die Komponenten der beiden Richtungsvektoren nicht proportional zueinander sind, sind die beiden Geraden also nicht parallel.

Und da die beiden Linien nicht parallel sind, bedeutet dies, dass es tatsächlich einen Schnittpunkt zwischen ihnen gibt. Um es zu berechnen, müssen wir das Gleichungssystem lösen, das durch die Gleichung jeder Geraden gebildet wird:

In diesem Fall wie die Zeile

in Form parametrischer Gleichungen vorliegt, muss der Ausdruck jeder parametrischen Gleichung in die Gleichung der anderen Zeile eingesetzt werden:

Lösen wir nun die resultierende Gleichung:

und ersetzen Sie den Wert von

finden Sie in den parametrischen Gleichungen, um die Koordinaten des Schnittpunkts zu finden:

Der Schnittpunkt der beiden Geraden ist also: