▷ Restsatz: Was es ist, Beispiele und gelöste Übungen ✅

Hier finden Sie die Erklärung, was der Restsatz (oder Restsatz) ist und wie er auf Polynome angewendet wird. Sie können sich auch Beispiele ansehen und zusätzlich mit Schritt-für-Schritt-Lösungen von Übungen zum Restsatz üben.

Was ist der Restsatz?

In der Mathematik besagt der Restsatz , dass der Rest der Division eines beliebigen Polynoms P(x) durch ein anderes Polynom der Form (xa) gleich dem numerischen Wert des Polynoms P(x) für den Wert x=a, In ist Mit anderen Worten, der Rest der Division P(x):(xa) ist äquivalent zu P(a).

Beispiel für den Restsatz

Nachdem wir den Restsatz gesehen haben, schauen wir uns ein praktisches Beispiel seiner Anwendung an:

Berechnen Sie den Rest der Division zwischen den folgenden zwei Polynomen:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

Um den Rest (oder Residuum) der Polynomdivision zu finden, können wir uns den Restsatz zunutze machen, denn in diesem Fall hat das Divisionspolynom die Form (xa), d. h. es ist vom ersten Grad, dem Koeffizienten von Die Variable x ist 1 und hat einen unabhängigen Term.

Daher wenden wir den Restsatz an, der besagt, dass der Rest einer solchen Division gleich dem numerischen Wert des Dividendenpolynoms ist, der im unabhängigen Term des vorzeichengeänderten Divisorpolynoms ausgewertet wird, also P (1).

Um den Rest der Division zu finden, müssen wir daher das Polynom bei x=1 auswerten:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

Der Rest der Division zwischen den Polynomen beträgt daher 2 .

Andererseits können wir auch mit Ruffinis Regel zur Division von Polynomen überprüfen, dass der Rest mit dem Ergebnis übereinstimmt, das wir gefunden haben:

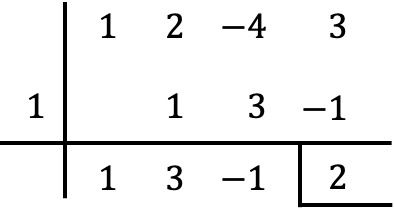
Wie Sie sehen, ist es mit dem Restsatz viel schneller und einfacher, den Rest einer Division eines Polynoms durch ein Binomial zu bestimmen als mit der Ruffini-Regel, da viel weniger Berechnungen durchgeführt werden müssen.

Rest- und Faktorsatz

Aus dem Restsatz und der Definition der Wurzel (oder Nullstelle) eines Polynoms können wir den Faktorsatz ableiten. Der Faktorsatz impliziert also Folgendes:

Der Faktorsatz besagt, dass ein Polynom P(x) genau dann durch ein anderes Polynom der Form (xa) teilbar ist, wenn P(a)=0. Und das bedeutet in diesem Fall, dass a eine Wurzel oder eine Nullstelle des Polynoms P(x) ist.

Darüber hinaus bedeutet dies nach dem Restsatz, dass, wenn ein Polynom durch ein anderes Polynom teilbar ist, der Rest dieser Division Null ist, da P(a)=0.

Wenn wir zum Beispiel ein bestimmtes Polynom haben:

$P(x)=x^2+2x-8$

Dieses Polynom ist durch das Binomial (x-2) teilbar, weil P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

Da x=2 das Polynom P(x) aufhebt, bedeutet dies, dass x=2 eine Wurzel dieses Polynoms ist.

Und da P(2)=0 ist, können wir dank des Restsatzes wissen, dass der Rest der Division

$\cfrac{x^2+2x-8}{x-2}$

ist gleich 0.

Gelöste Übungen zum Restsatz

Um das Verständnis des Restsatzes zu vervollständigen, haben wir einige Übungen vorbereitet, die Schritt für Schritt gelöst werden, damit Sie sie üben können. Wir empfehlen Ihnen, die Übung zunächst selbst auszuprobieren und dann zu überprüfen, ob Sie sie richtig ausgeführt haben.

Übung 1

Finden Sie mit dem Restsatz den Rest der Polynomdivision

$\cfrac{P(x)}{Q(x)}$

, wobei es sich um die an der Operation beteiligten Polynome handelt:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

Sehen Sie sich die Lösung an

Das Divisorpolynom besteht nur aus einem Term ersten Grades und einem unabhängigen Term und außerdem ist der Koeffizient des Termes ersten Grades 1. Wir können daher den Restsatz verwenden.

Und um den Restsatz anzuwenden, reicht es aus, das Dividendenpolynom im unabhängigen Term des Divisorpolynoms mit geändertem Vorzeichen auszuwerten, oder mit anderen Worten, wir müssen P(2) berechnen.

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

Der Rest der Division zwischen den beiden Polynomen beträgt daher 21 .

Übung 2

Gegeben sei das Polynom

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

Finden Sie den Rest, den Sie erhalten, indem Sie ihn durch jedes der folgenden Polynome dividieren:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

Sehen Sie sich die Lösung an

Da alle Divisionspolynome die Bedingungen des Restsatzes erfüllen, können wir diesen Satz verwenden, um den Rest jeder Division zu bestimmen:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

Übung 3

Berechnen Sie, wie viel der Parameter wert sein sollte

$m$

damit ist der Rest der Division von Polynomen

$\cfrac{P(x)}{Q(x)}$

gleich 3 sein, da beide Polynome sind:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

Sehen Sie sich die Lösung an

In diesem speziellen Fall besteht das dividierende Polynom aus einem Monom ersten Grades und einem unabhängigen Term und außerdem ist der Koeffizient des Monoms ersten Grades 1. Wir können daher den Restsatz verwenden.

Und um den Restsatz zu verwenden, ersetzen Sie einfach den unabhängigen Term des dividierenden Polynoms durch einen Vorzeichenwechsel, bei dem es im dividierten Polynom ein x gibt, wir müssen also P(-3) lösen.

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$

Aber offensichtlich erhalten wir ein Ergebnis, das auf dem Unbekannten basiert

$m.$

Die Problemstellung sagt uns jedoch, dass der Rest gleich drei sein muss, also müssen wir den gefundenen Rest gleich 3 setzen:

$3m-63 = 3$

Und schließlich lösen wir die Gleichung:

$3m = 3+63$

$3m = 66$

$m = \cfrac{66}{3}$

$\bm{m = 22}$

Übung 4

Bestimmen Sie mit dem Faktor- und Restsatz, ob das Polynom vorliegt

$P(x)$

ist durch das Polynom teilbar

$Q(x).$

$P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2$

Sehen Sie sich die Lösung an

Damit das Polynom

$P(x)$

durch das Polynom teilbar sein

$Q(x)$

Die Division zwischen diesen beiden Polynomen muss exakt sein und daher muss der Rest Null sein.

Dann ist das Teilerpolynom

$(x+2),$

Durch den Faktorsatz und den Restsatz wissen wir, dass das Polynom

$P(x)$

wird durch das Polynom teilbar sein

$Q(x)$

wenn es gefüllt ist

$P(-2)=0.$

Wir müssen daher prüfen, ob diese Gleichheit bestätigt ist:

$P(-2)=0 \quad \color{blue} \bm{?}$

$\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}$

In der Tat, der Rest der Division

$\cfrac{P(x)}{Q(x)}$

ist gleich 0, also das Polynom

$P(x)$

Ja, es ist durch das andere Polynom teilbar

$Q(x).$

Was halten Sie von der Erklärung? Hat es Ihnen gefallen? Hoffen wir es mal! Vergessen Sie nicht, dass Sie uns Ihre Vorschläge oder Fragen in den Kommentaren hinterlassen können. ⬇⬇⬇ Wir lesen euch alle! 😁😁

Restsatz (oder restsatz).

Was ist der Restsatz?

Beispiel für den Restsatz

Rest- und Faktorsatz

Gelöste Übungen zum Restsatz

Übung 1

Übung 2

Übung 3

Übung 4

Kommentar verfassen Kommentieren abbrechen