Antisymmetrische Matrix

Auf dieser Seite erklären wir, was antisymmetrische Matrizen sind. Darüber hinaus können Sie mehrere Beispiele sowie die typische Struktur sehen, um es perfekt zu verstehen. Wir erklären auch die Besonderheit der Berechnung der Determinante einer antisymmetrischen Matrix und alle Eigenschaften dieses Matrixtyps. Und schließlich erfahren Sie, wie Sie jede quadratische Matrix in die Summe einer symmetrischen Matrix und einer weiteren antisymmetrischen Matrix zerlegen.

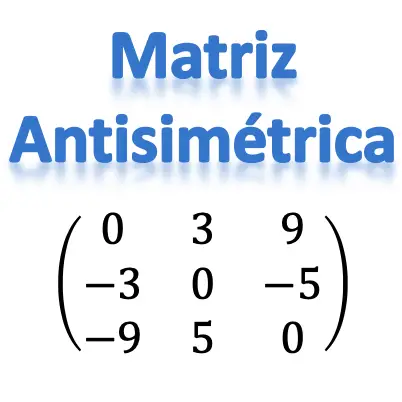
Was ist eine antisymmetrische Matrix?

Die Definition einer antisymmetrischen Matrix lautet wie folgt:

Eine antisymmetrische Matrix ist eine quadratische Matrix, deren Transponierte gleich dem Negativ der Matrix ist.

$A^t = -A$

Gold

$A^t$

stellt die transponierte Matrix von dar

$A$

Und

$-A$

ist die Matrix

$A$

mit allen seinen Elementen geändertes Vorzeichen.

Beispiele für antisymmetrische Matrizen

Sobald wir das Konzept der antisymmetrischen Matrix kennen, werden wir zum besseren Verständnis mehrere Beispiele antisymmetrischer Matrizen sehen:

Beispiel einer antisymmetrischen Matrix der Ordnung 2 × 2

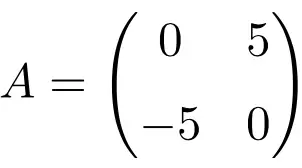
Beispiel einer antisymmetrischen Matrix der Dimension 2x2

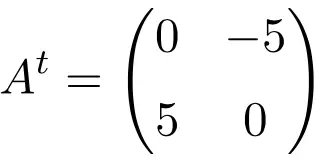
Übung zur antisymmetrischen Matrix der Dimension 2x2 gelöst

Beispiel einer antisymmetrischen Matrix der Dimension 3×3

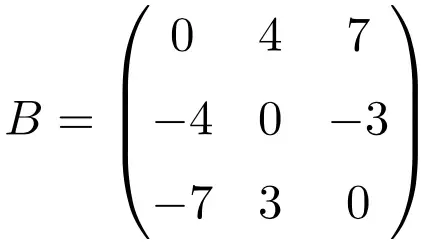
Beispiel einer antisymmetrischen Matrix der Dimension 3x3

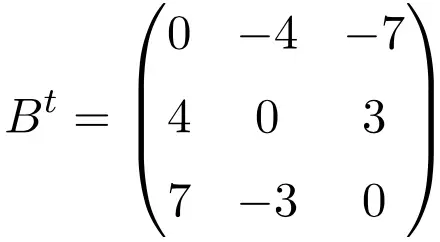
Übung zur antisymmetrischen Matrix der Dimension 3x3 gelöst

Beispiel einer antisymmetrischen Matrix der Größe 4×4

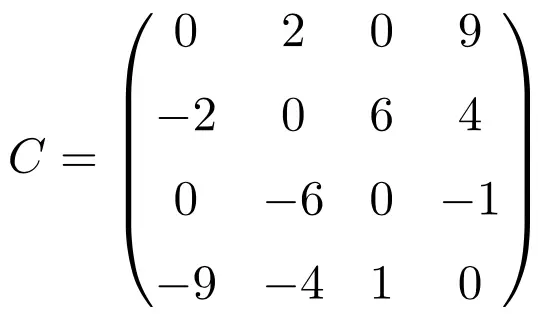
Beispiel einer antisymmetrischen Matrix der Dimension 4x4

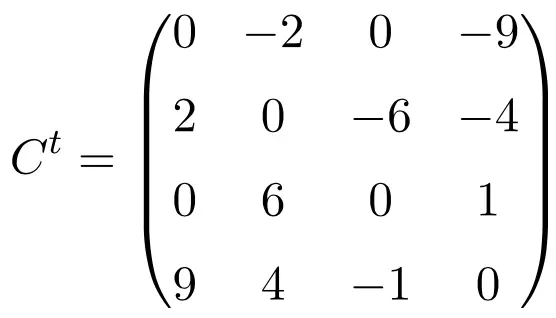
Übung zur antisymmetrischen Matrix der Dimension 4x4 gelöst

Bei der Transponierung dieser drei Matrizen stellen wir sicher, dass sie antisymmetrisch sind, da die transponierten Matrizen ihren jeweiligen ursprünglichen Matrizen mit geändertem Vorzeichen entsprechen.

Struktur einer antisymmetrischen Matrix

Damit die antisymmetrische Matrixbedingung erfüllt ist, müssen sie immer den gleichen Strukturtyp haben: Die Zahlen auf der Hauptdiagonalen sind alle gleich Null und das Element von Zeile i und Spalte j ist das Negative des Elements von Zeile j und Spalte ich . Mit anderen Worten, die Form der antisymmetrischen Matrizen ist wie folgt:

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

Daher fungiert die Hauptdiagonale einer antisymmetrischen Matrix als Antisymmetrieachse. Daher kommt auch der Name dieser besonderen Matrix.

Determinante einer antisymmetrischen Matrix

Die Determinante einer antisymmetrischen Matrix hängt von der Dimension dieser Matrix ab. Dies liegt an den Eigenschaften der Determinanten:

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

Wenn die antisymmetrische Matrix also eine ungerade Ordnung hat, ist ihre Determinante gleich 0 . Wenn andererseits die antisymmetrische Matrix eine gerade Dimension hat, kann die Determinante jeden Wert annehmen.

Daher ist eine antisymmetrische Matrix ungerader Dimension eine singuläre oder entartete Matrix. Andererseits ist eine antisymmetrische Matrix gerader Ordnung eine reguläre Matrix.

Eigenschaften antisymmetrischer Matrizen

Die Eigenschaften antisymmetrischer Matrizen sind wie folgt:

Die Addition (oder Subtraktion) zweier antisymmetrischer Matrizen ergibt eine weitere antisymmetrische Matrix. Da das Transponieren zweier addierter (oder subtrahierter) Matrizen dem Transponieren jeder Matrix einzeln entspricht:

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

Jede mit einem Skalar multiplizierte antisymmetrische Matrix führt auch zu einer anderen antisymmetrischen Matrix.

Die Potenz einer antisymmetrischen Matrix entspricht einer antisymmetrischen Matrix oder einer symmetrischen Matrix. Wenn der Exponent eine gerade Zahl ist, ist das Potenzergebnis eine symmetrische Matrix. Wenn der Exponent jedoch eine ungerade Zahl ist, ist das Potenzergebnis eine antisymmetrische Matrix. Unter diesem Link können Sie nachlesen , was eine symmetrische Matrix ist .

Die Spur einer antisymmetrischen Matrix ist immer gleich Null.

Die Summe einer antisymmetrischen Matrix plus der Einheitsmatrix ergibt eine invertierbare Matrix.

$\displaystyle \text{det}(A+I)\neq 0$

Alle reellen Eigenwerte (oder Eigenwerte) einer antisymmetrischen Matrix sind 0. Eine antisymmetrische Matrix kann jedoch auch komplexe Eigenwerte haben.

Alle antisymmetrischen Matrizen sind Normalmatrizen. Daher unterliegen sie dem Spektralsatz, der besagt, dass eine antisymmetrische Matrix durch eine einheitliche Matrix diagonalisiert werden kann.

Zerlegung einer quadratischen Matrix in eine symmetrische Matrix und eine antisymmetrische Matrix

Eine Besonderheit quadratischer Matrizen besteht darin, dass sie in die Summe einer symmetrischen Matrix plus einer antisymmetrischen Matrix zerlegt werden können.

Die Formel, die uns dies ermöglicht, lautet wie folgt:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Wobei C die quadratische Matrix ist, die wir zerlegen möchten, C ^t ihre Transponierte und schließlich S und A die symmetrischen bzw. antisymmetrischen Matrizen sind, in die die Matrix C zerlegt wird.

Nachfolgend finden Sie eine gelöste Übung zur Veranschaulichung der Formel. Zerlegen wir die folgende Matrix:

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

Wir berechnen die symmetrische und antisymmetrische Matrix mit den Formeln:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

Und wir können überprüfen, ob die Gleichung erfüllt ist, indem wir die beiden Matrizen addieren:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$

✅

Antisymmetrische matrix