Auf dieser Seite finden Sie die Erklärung ähnlicher Matrizen, auch ähnliche Matrizen genannt. Darüber hinaus zeigen wir Ihnen ein anschauliches Beispiel zweier ähnlicher Matrizen und alle Eigenschaften dieser Art von Matrizen, damit Sie keine Zweifel haben. Schließlich können Sie sogar sehen, wie sie sich auf kongruente Matrizen beziehen.
Was sind ähnliche (oder ähnliche) Matrizen?
Die Definition ähnlicher Matrizen lautet wie folgt:
zwei Matrizen
![]()
Und
![]()
sind ähnlich (oder ähnlich), wenn eine Matrix existiert
![]()
womit folgende Bedingung erfüllt ist:
![]()
Oder gleichwertig:
![]()
Tatsächlich die Matrix
![]()
fungiert als Basis-Änderungsmatrix. Daher bedeutet diese Gleichung, dass die Matrix
![]()
kann in einer anderen Basis ausgedrückt werden (
![]()
), wodurch die Matrix entsteht
![]()
.
Dieser Begriff kann auch als Ähnlichkeitstransformation bezeichnet werden, da wir tatsächlich die Matrix transformieren
![]()
in der Matrix
![]()
.
Offensichtlich die Matrix
![]()
es muss eine reguläre oder nicht entartete Matrix sein (Determinante ungleich Null).
Andererseits können wir angeben, dass zwei Matrizen dem folgenden Ausdruck ähneln:
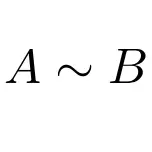
Diese Matrizenklasse ist für die lineare Algebra wichtiger als es scheint. Sie werden hauptsächlich für diagonalisierbare Matrizen verwendet, da das Verfahren zur Diagonalisierung einer beliebigen Matrix auf dem Konzept der Matrixähnlichkeit basiert.
Tatsächlich beinhaltet der Prozess der Diagonalisierung einer Matrix die Berechnung einer ähnlichen Matrix, die gleichzeitig eine Diagonalmatrix ist. Wie das geht, können Sie im Artikel „Diagonalisieren einer Matrix“ sehen.
Beispiel für ähnliche oder ähnliche Matrizen
Anschließend sehen wir uns ein Beispiel ähnlicher Matrizen der Dimension 2×2 an, um die Assimilation des Konzepts abzuschließen.
- Die quadratischen Matrizen A und B ähneln einander durch die invertierbare Matrix P:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4978e1117b69063b63256a0663eaf207_l3.png)
![Rendered by QuickLaTeX.com \displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6344f1d5a14dd381ab105bcb52827455_l3.png)
Um zu zeigen, dass es sich hierbei um zueinander ähnliche Matrizen handelt, müssen wir zunächst die inverse Matrix von P berechnen:
![Rendered by QuickLaTeX.com \displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49a4a995246e782635e2e2b43302798_l3.png)
Und jetzt überprüfen wir, ob sie ähnlich sind, indem wir das Matrixprodukt berechnen, das die Ähnlichkeit zweier Matrizen definiert:
![]()
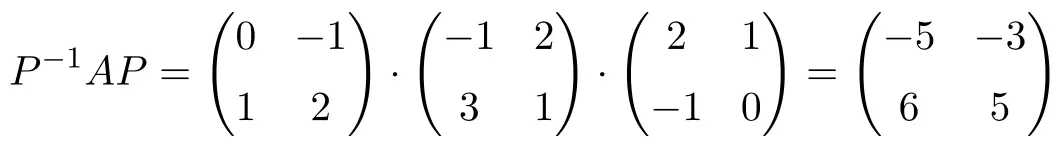
![]()
✅
Ja, die Ähnlichkeitsrelation ist erfüllt, es handelt sich also um ähnliche Matrizen.
Ähnliche Matrixeigenschaften
Zwei ähnliche Matrizen A und B haben die folgenden Merkmale gemeinsam:
- Gleicher Rang.
![]()
- Die Determinanten der beiden Matrizen sind gleich.
![]()
- Gleiche Ablaufverfolgung.
![]()
- Gleiche Eigenwerte (oder Eigenwerte). Allerdings sind die Eigenvektoren (bzw. Eigenvektoren) meist unterschiedlich.
- Gleiches charakteristisches Polynom und minimales Polynom.
- Das Transponieren einer Matrix ähnelt der ursprünglichen Matrix.
- Matrix B kann durch Anwenden elementarer Operationen auf die Zeilen von Matrix A gefunden werden und umgekehrt.
- Offensichtlich spiegelt sich die Ähnlichkeit wider. Das heißt, wenn A B ähnlich ist, dann ist B auch A ähnlich.
- Darüber hinaus ist auch die Ähnlichkeit der Matrizen symmetrisch. Mit anderen Worten: Wenn mit der Matrix P die Matrix erhalten werden kann, die A (B) ähnlich ist, kann mit derselben Matrix P auch die Matrix erhalten werden, die B (A) ähnlich ist:
![]()
![]()
- Darüber hinaus ist Ähnlichkeit transitiv. Wenn also Matrix A Matrix B ähnlich ist und Matrix B Matrix C ähnlich ist, ist Matrix A auch Matrix C ähnlich.
![Rendered by QuickLaTeX.com \left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9f845ee4a4c9e72220ecb4033ea9640_l3.png)
- Schließlich ähnelt jede Matrize einer Sägezahnmatrize. Und aus dieser Eigenschaft können wir die folgende Folgerung ableiten: Jede quadratische Matrix ähnelt einer dreieckigen Matrix.
kongruente Matrizen
Andererseits gibt es auch eine andere, sehr ähnliche Beziehung zwischen Matrizen, allerdings nicht mit der inversen Matrix, sondern mit der transponierten Matrix. Dies nennt man Kongruenz .
Zwei Matrizen A und B sind kongruent , wenn es eine invertierbare Matrix P gibt, mit der die folgende Gleichung erfüllt ist:
![]()
Wie Sie sehen können, ist dies das Analogon ähnlicher Matrizen, jedoch mit transponierter Matrix.