Sich kreuzende Linien

Auf dieser Seite finden Sie alles über Sekantenlinien: Was sie bedeuten, welche verschiedenen Typen es gibt, wie man erkennt, ob zwei Linien Sekanten sind, wie man ihren gemeinsamen Punkt findet, … Außerdem können Sie sich mehrere Beispiele und gelöste Übungen ansehen von Sekantenlinien.

Was sind zwei Schnittlinien?

In der Mathematik lautet die Definition von Sekantenlinien wie folgt:

Zwei Geraden schneiden sich, wenn sie sich nur in einem Punkt schneiden. Schnittlinien haben daher nur einen gemeinsamen Punkt. Darüber hinaus müssen zwei sich schneidende Linien notwendigerweise in derselben kartesischen Ebene liegen.

Das Konzept, dass sich zwei Geraden in einem einzigen Punkt schneiden, ist wichtig, denn wenn sie mehr als einen Schnittpunkt hätten, wären sie zusammenfallende Geraden, und wenn sie andererseits keinen Schnittpunkt hätten, wären sie parallele Geraden.

Beispiele für sich kreuzende Linien

Nachdem wir die Bedeutung zweier sich kreuzender Linien gesehen haben, schauen wir uns nun zwei verschiedene Beispiele dieser Art von Linien an:

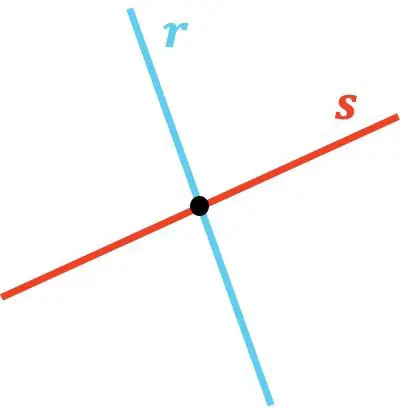
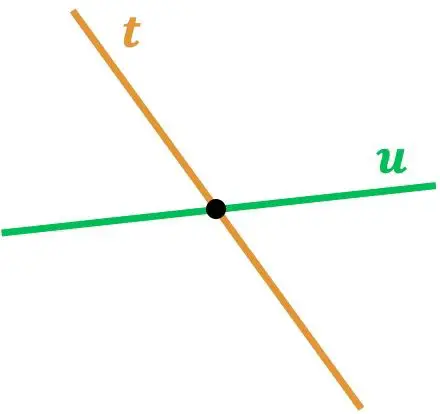
Wie Sie sehen, schneiden sich die Linien r und s , weil sie sich in einem Punkt berühren. Und auf die gleiche Weise schneidet die Linie t die Linie u , da es einen Punkt gibt, an dem sie sich schneiden.

Arten von Schnittlinien

Es gibt zwei Arten von Schnittlinien:

Senkrechte Linien : sind Linien, die sich im rechten Winkel von 90° schneiden.
Schräge Linien: bestehen aus Linien, die sich in einem spitzen Winkel zwischen 0° und 90° schneiden (nicht enthalten).

Senkrechte gerade Linien

Senkrechte Linien sind Linien, die sich schneiden und vier 90-Grad-Winkel bilden.

Ebenso erfüllen die Steigungen zweier senkrechter Geraden immer die folgende Bedingung:

$m_r = -\cfrac{1}{m_s}$

Eine weitere Eigenschaft sich senkrecht schneidender Linien besteht darin, dass das Skalarprodukt zwischen ihren Richtungsvektoren (ein Vektor, der die Richtung einer Linie angibt) gleich Null ist.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

Wenn Sie sich mehr für senkrechte Linien interessieren, finden Sie unter diesem Link Beispiele für senkrechte Linien . Darüber hinaus erfahren Sie, wie Sie eine Linie senkrecht zu einer anderen berechnen, welche Eigenschaften diese Art von Linie hat, wie Sie Schritt für Schritt Übungen lösen usw.

schräge Linien

Schräge Linien sind Linien, die sich schneiden und paarweise spitze und stumpfe Winkel bilden. Das heißt, zwei spitze Winkel (weniger als 90°) und zwei stumpfe Winkel (größer als 90°) bilden. Nach der Definition des Winkels zweier Geraden ist jedoch der Winkel zwischen zwei Geraden der kleinste der durch ihn gebildeten Winkel.

Der Winkel zwischen zwei schrägen Linien mit ihren Steigungen kann mit der folgenden Formel berechnet werden:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Woher wissen Sie, ob sich zwei Geraden schneiden?

Es gibt hauptsächlich drei Methoden, um die relative Position zweier Linien zu ermitteln:

Mit den Richtungsvektoren der beiden Geraden.
Mit den Steigungen der beiden Linien.
Mit der impliziten (oder allgemeinen) Gleichung der beiden Geraden.

Dann sehen wir uns die Erklärung der drei Methoden an, die es gibt, um zu wissen, wann sich zwei Linien schneiden.

Aus den Richtungsvektoren der Linien

Wenn die Koordinaten der Richtungsvektoren (Vektor, die die Richtung einer Linie markieren) zweier verschiedener Linien nicht proportional sind , schneiden sich diese beiden Linien.

Sehen wir uns eine Übung an, die Schritt für Schritt mit zwei sich schneidenden Linien gelöst wird:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

Beide Linien werden als parametrische Gleichungen ausgedrückt, sodass die Komponenten des Richtungsvektors jeder Linie die Zahlen vor dem Parameter sind

$t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

Um also zu sehen, ob die Richtungsvektoren proportional sind, müssen wir ihre Koordinaten untereinander aufteilen. Wenn wir in beiden Divisionen das gleiche Ergebnis erhalten, sind sie proportional; Ist das Ergebnis hingegen unterschiedlich, bedeutet dies, dass die Vektoren nicht proportional sind.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

Die Teilungen der Komponenten sind nicht äquivalent, daher sind die Vektoren nicht proportional und daher schneiden sich die Geraden.

am Anfang der Pisten

Wenn zwei Geraden unterschiedliche Steigungen haben, bedeutet dies, dass sich die Geraden schneiden.

Beispielsweise schneiden sich die beiden folgenden Geraden, weil sie unterschiedliche Steigungen haben:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

Die Steigung der Linie

$r$

ist -2 und die Steigung der Geraden

$s$

ist 3.

$m_r =-2 \neq m_s =3$

Da die beiden Geraden nicht die gleiche Steigung haben, schneiden sie sich.

Aus der impliziten Gleichung der Geraden

Durch die impliziten Gleichungen (oder allgemeinen Gleichungen) der Geraden lässt sich auch herausfinden, ob sich zwei Geraden schneiden oder nicht. Die implizite Gleichung der Geraden lautet wie folgt:

$Ax+By+C=0$

Somit schneiden sich zwei Geraden, wenn ihre Koeffizienten A und B nicht proportional sind.

Sehen wir uns ein Beispiel für zwei sich schneidende Linien an, die mit ihrer impliziten Gleichung definiert sind:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

Um zu überprüfen, ob es sich um zwei Schnittlinien handelt, müssen wir die Proportionalität des Koeffizienten A (Zahl vor der Variablen) analysieren

$x$

) mit dem Koeffizienten B (Ziffer vor der Variablen).

$y$

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

Die beiden Terme sind nicht proportional, sodass sich die beiden Geraden effektiv schneiden.

Finden Sie den gemeinsamen Punkt zweier Schnittlinien

Wie wir gesehen haben, haben sich schneidende Geraden nur einen gemeinsamen Punkt. Um den Schnittpunkt zweier Sekantenlinien zu berechnen , ist es daher notwendig, das durch die beiden Linien gebildete Gleichungssystem zu lösen.

Als Beispiel finden wir den Schnittpunkt der folgenden zwei Geraden:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

Um den Schnittpunkt der beiden Geraden zu bestimmen, müssen wir das durch die beiden Geraden gebildete lineare Gleichungssystem lösen:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

In diesem Fall lösen wir das System mit der Substitutionsmethode. Wir werden daher die Variable isolieren

$x$

aus der ersten Gleichung und setze es in die zweite Gleichung ein:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

Und sobald wir wissen, wie viel das Unbekannte wert ist

$y$

Wir setzen seinen Wert in den gefundenen Ausdruck ein

$x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

Die Lösung des Gleichungssystems ist daher der Schnittpunkt der beiden Geraden. Und dieser Punkt ist

$\bm{(3,1)}.$

Linie, die einen Kreis schneidet

Wenn wir sagen, dass sich zwei Linien schneiden, beziehen wir uns normalerweise auf das Konzept, das wir gerade gesehen haben. In der Geometrie gibt es jedoch noch eine andere Bedeutung der Sekantenlinie:

Eine Linie, die einen Kreis schneidet, ist eine Linie, die einen Kreis (oder eine Kurve) an zwei verschiedenen Punkten schneidet.

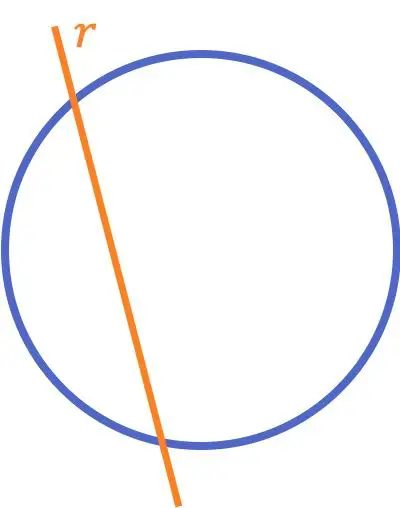
Anders als das Konzept zweier sich schneidender Linien, das normalerweise in der Grundschule gelehrt wird, wird diese Definition einer Linie, die einen Kreis schneidet, in späteren Klassen oft zusammen mit allen relativen Positionen von Linien und Kreisen studiert.