Auf dieser Seite finden Sie die Erklärung der Regel (oder des Gesetzes) des Parallelogramms. Darüber hinaus sehen Sie mehrere Beispiele für die Addition und Subtraktion von Vektoren mithilfe der Parallelogrammregel sowie reale Anwendungen.
Was ist die Parallelogrammregel?
Wie Sie bereits wissen, können Vektorgrößen nicht auf die gleiche Weise wie reelle Zahlen addiert oder subtrahiert werden, da sie zwei Komponenten (in R2) oder drei Komponenten (in R3) haben und weil Vektoren unterschiedliche Richtungen haben können. Daher sind andere Methoden erforderlich, um Vektoroperationen durchzuführen, beispielsweise die Parallelogrammregel, die aus Folgendem besteht:
In der Mathematik ist die Parallelogrammregel ein Verfahren zum Addieren oder Subtrahieren zweier Vektoren zu ihrer grafischen Darstellung.
Die Parallelogramm-Methode wird bei der Addition und Subtraktion von Vektoren (grafisch) sicherlich am häufigsten verwendet, da es sich um eine sehr einfach anzuwendende Technik handelt. In der Physik wird es beispielsweise zum Addieren und Subtrahieren von Kräften verwendet.
Andererseits variiert die Regel leicht, je nachdem, ob wir Vektoren addieren oder subtrahieren möchten, daher werden wir im Folgenden beide Versionen separat erklären.
Parallelogrammregel zum Addieren zweier Vektoren
Wenn wir zwei Vektoren grafisch addieren möchten, sind die Schritte zur Anwendung der Parallelogrammregel oder des Parallelogrammgesetzes wie folgt:
- Zuerst zeichnen wir die Vektoren und positionieren sie am gleichen Anwendungspunkt, das heißt, wir platzieren die Ursprünge beider Vektoren am gleichen Punkt.
- Dann zeichnen wir am Ende eines Vektors eine Linie parallel zum anderen Vektor. Und wir wiederholen den Schritt mit dem anderen Vektor. Wir erhalten also die Zeichnung eines Parallelogramms (daher der Name der Regel).
- Der aus der Summe resultierende Vektor ist schließlich die Diagonale des Parallelogramms, die vom gemeinsamen Ursprung der Vektoren zum Schnittpunkt der beiden parallelen Geraden verläuft.
Im folgenden generischen Beispiel können Sie sehen, wie die Parallelogrammregel verwendet wird:

Wenn Sie mit der Parallelogrammregel üben möchten, können Sie unter dem folgenden Link weitere Beispiele und mehrere gelöste Vektoradditionsübungen einsehen. Auf dieser Seite finden Sie auch andere Methoden zum grafischen Hinzufügen von Vektoren und sogar die numerische Addition von Vektoren.
Parallelogrammregel zum Subtrahieren zweier Vektoren
Die Parallelogrammregel oder -methode wird auch verwendet, um zwei Vektoren von einem Diagramm zu subtrahieren. Die Schritte zur Vektorsubtraktion sind also:
- Zuerst stellen wir die beiden Vektoren im Diagramm dar und positionieren sie am gleichen Anwendungspunkt, das heißt, wir platzieren die Ursprünge beider Vektoren am gleichen Punkt.
- Zweitens zeichnen wir den entgegengesetzten Vektor des Vektors, der in der Operation subtrahiert wird, oder mit anderen Worten, wir kehren den Vektor um, der subtrahiert.
- Dann zeichnen wir am Ende des Vektors eine Linie parallel zum Vorzeichenwechselvektor, die sich zu ergibt. Und wir wiederholen den Vorgang mit dem anderen Vektor. Damit erhalten wir die Zeichnung eines Parallelogramms (daher der Name der Regel).
- Das Ergebnis der Subtraktion ist schließlich der Vektor, der vom gemeinsamen Ursprung der beiden Vektoren bis zum Schnittpunkt der beiden parallelen Linien verläuft.
Schauen Sie sich das folgende allgemeine Beispiel an, in dem zwei Vektoren durch das Parallelogrammgesetz subtrahiert werden:
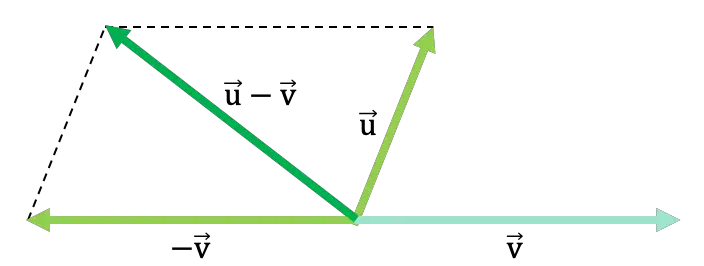
Im folgenden Link sehen Sie weitere Beispiele zur Vektorsubtraktion mit der Parallelogrammregel, Sie können auch mit gelösten Vektorsubtraktionsübungen üben. Darüber hinaus finden Sie weitere Techniken zum Subtrahieren von Vektoren aus ihrem Diagramm und schließlich, wie sie numerisch subtrahiert werden.
Wenn Ihnen die Erklärung dieser Technik nützlich war, werden Sie sicherlich auch daran interessiert sein, die Rechtshandregel zu kennen. Auf der Linkseite können Sie sehen, was es ist, für welche Vektoroperation sie verwendet wird und welche verschiedenen Variationen dieser Regel existieren.