Orthogonale Matrix

Auf dieser Seite erfahren Sie, was orthogonale Matrizen sind und welche Beziehung sie zur Umkehrung einer Matrix haben. Sie werden auch einige Beispiele sehen, um es perfekt zu verstehen. Darüber hinaus bringen wir Ihnen die Formel zur Überprüfung jeder orthogonalen Matrix bei, mit der Sie schnell eine finden können. Und schließlich finden Sie die Eigenschaften und Anwendungen dieser speziellen Matrizen sowie eine typische gelöste Prüfungsaufgabe.

Was ist eine orthogonale Matrix?

Die Definition einer orthogonalen Matrix lautet wie folgt:

Eine orthogonale Matrix ist eine quadratische reelle Zahlenmatrix, die multipliziert mit ihrer Transponierten (oder Transponierten) der Identitätsmatrix entspricht. Das heißt, die folgende Bedingung ist erfüllt:

$A\cdot A^t = A^t \cdot A =I$

Gold

$A$

ist eine orthogonale Matrix und

$A^t$

repräsentiert seine transponierte Matrix.

Damit diese Bedingung erfüllt ist, müssen die Spalten und Zeilen einer orthogonalen Matrix orthogonale Einheitsvektoren sein, das heißt, sie müssen eine Orthonormalbasis bilden. Manche Mathematiker nennen sie deshalb auch Orthonormalmatrizen .

Umkehrung einer orthogonalen Matrix

Eine andere Möglichkeit, das Konzept einer orthogonalen Matrix zu erklären, ist die inverse Matrix, da die transponierte (oder transponierte) Matrix einer orthogonalen Matrix gleich ihrer Umkehrung ist.

Um diesen Satz vollständig zu verstehen, ist es wichtig, dass Sie wissen, wie man eine Matrix invertiert . Unter diesem Link finden Sie eine detaillierte Erklärung der Umkehrung einer Matrix, aller ihrer Eigenschaften und Sie haben sogar Schritt-für-Schritt-Übungsaufgaben zum Üben gelöst.

Mithilfe der Orthogonalmatrixbedingung und der Haupteigenschaft inverser Matrizen kann leicht gezeigt werden, dass die inverse Matrix einer orthogonalen Matrix ihrer Transponierten äquivalent ist:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Daher ist eine orthogonale Matrix immer eine invertierbare Matrix , oder mit anderen Worten, es wird eine reguläre oder nicht entartete Matrix sein.

Als nächstes werden wir einige Beispiele orthogonaler Matrizen sehen, um das Konzept von allem besser zu verstehen.

Beispiel einer orthogonalen 2×2-Matrix

Die folgende Matrix ist eine orthogonale Matrix der Dimension 2×2:

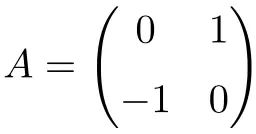
Wir können überprüfen, ob es orthogonal ist, indem wir das Produkt durch seine Transponierte berechnen:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Da das Ergebnis die identische Matrix ergibt, überprüfen wir, dass A eine orthogonale Matrix ist.

Beispiel einer orthogonalen 3×3-Matrix

Die folgende Matrix ist eine orthogonale Matrix der Dimension 3×3:

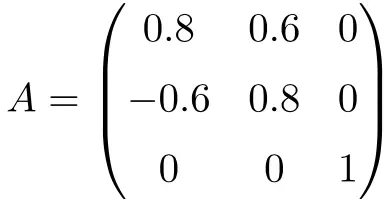
Wir können zeigen, dass sie orthogonal ist, indem wir die Matrix A mit ihrer Transponierten multiplizieren:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Da die Lösung die Einheitsmatrix ist, zeigen wir, dass A eine orthogonale Matrix ist.

Formel zum Finden einer orthogonalen 2×2-Matrix

Wir werden dann den Beweis sehen, dass alle orthogonalen Matrizen der Ordnung 2 dem gleichen Muster folgen.

Betrachten Sie eine generische Matrix der Größe 2×2:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Damit diese Matrix orthogonal ist, muss die folgende Matrixgleichung erfüllt sein:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Wenn wir die Matrixmultiplikation lösen, erhalten wir die folgenden Gleichungen:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Wenn man genau hinschaut, ähneln diese Gleichungen stark der grundlegenden trigonometrischen Beziehung des Pythagoras :

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Folglich sind die Terme, die die Gleichungen (1) und (3) erfüllen, erhalten:

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

Durch Einsetzen der Werte in die zweite Gleichung erhalten wir außerdem die Beziehung zwischen den beiden Winkeln:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

Das heißt, eine der beiden folgenden Bedingungen muss erfüllt sein:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Zusammenfassend lässt sich sagen, dass orthogonale Matrizen die Struktur einer der beiden folgenden Matrizen haben müssen:

Formel für die orthogonale Matrix der Dimension 2x2

Gold

$\theta$

ist eine reelle Zahl.

In der Tat, wenn wir als Beispiel den Wert gewähren

$\displaystyle\theta=\frac{\pi}{2}$

und wenn wir die erste Struktur nehmen, erhalten wir die Matrix, deren Orthogonalität wir im Abschnitt „Beispiel einer orthogonalen 2×2-Matrix“ überprüft haben:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Orthogonale Matrixeigenschaften

Die Merkmale dieses Matrixtyps sind:

Eine orthogonale Matrix kann niemals eine singuläre Matrix sein, da sie immer invertiert werden kann. In diesem Sinne ist die Umkehrung einer orthogonalen Matrix eine andere orthogonale Matrix.

Jede orthogonale Matrix kann diagonalisiert werden. Wir sagen dann, dass orthogonale Matrizen orthogonal diagonalisierbar sind.

Alle Eigenwerte oder Eigenwerte einer orthogonalen Matrix haben einen Modul gleich 1.

Jede orthogonale Matrix, die nur aus reellen Zahlen besteht, ist auch eine Normalmatrix.

Das Analogon der orthogonalen Matrix in einer Umgebung mit komplexen Zahlen ist die Einheitsmatrix.

Offensichtlich ist die Identitätsmatrix eine orthogonale Matrix.

Die Menge der orthogonalen Matrizen der Dimension n × n sowie die Operation des Matrixprodukts bilden eine Gruppe namens orthogonale Gruppe. Das heißt, das Produkt zweier orthogonaler Matrizen ist gleich einer anderen orthogonalen Matrix.

Darüber hinaus kann das Ergebnis der Multiplikation einer orthogonalen Matrix mit ihrer Transponierten durch das Kronecker-Delta ausgedrückt werden:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Schließlich ist die Determinante einer orthogonalen Matrix immer +1 oder -1.

$\displaystyle \text{det}(A)=\pm 1$

Gelöste Übung zu orthogonalen Matrizen

Anschließend lösen wir eine Übung zu orthogonalen Matrizen.

Ermitteln Sie anhand der folgenden quadratischen Matrix der Ordnung 3 die Werte von
$a$

Und

$b$

um es orthogonal zu machen:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Damit die Orthogonalität der Matrix erfüllt ist, muss das Produkt der Matrix mit ihrer Transponierten gleich der Identitätsmatrix sein. ALSO:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

Wir multiplizieren die Matrizen:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

Wir können nun eine Gleichung aus der oberen linken Ecke der Matrizen erhalten, da die Elemente an dieser Position übereinstimmen müssen. Noch:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

Wir lösen die Gleichung und eliminieren die Unbekannte:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

Allerdings gibt es Gleichungen, die mit der positiven Lösung nicht zutreffen, zum Beispiel die in der oberen rechten Ecke. Es ist also nur die negative Lösung möglich .

Andererseits, um die Variable zu berechnen

$b$

Wir können beispielsweise die Begriffe in der zweiten Zeile der ersten Spalte zuordnen:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

Durch Ersetzen des Wertes von

$a$

in der Gleichung:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

Kurz gesagt, die einzig mögliche Lösung ist:

$\displaystyle \bm{a=b =-2}$

Die orthogonale Matrix, die diesen Werten entspricht, ist also:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Anwendungen orthogonaler Matrizen

Auch wenn es nicht so scheint, weil sie normalerweise eine sehr einfache Form haben, sind orthogonale Matrizen in der Mathematik, insbesondere im Bereich der linearen Algebra, sehr wichtig.

In der Geometrie stellen orthogonale Matrizen isometrische Transformationen (die Abstände und Winkel nicht ändern) in realen Vektorräumen dar, weshalb sie orthogonale Transformationen genannt werden. Darüber hinaus handelt es sich bei diesen Transformationen um interne Isomorphismen des betrachteten Vektorraums. Diese Transformationen können Rotationen , Spiegelreflexionen oder Inversionen sein.

Schließlich wird diese Art von Matrix auch in der Physik verwendet, da sie die Untersuchung der Bewegung starrer Körper ermöglicht. Und sie werden sogar bei der Formulierung bestimmter Feldtheorien verwendet.