Auf dieser Seite erfahren Sie, was koplanare (oder koplanare) Punkte sind und wie Sie feststellen können, ob bestimmte Punkte koplanar sind oder nicht. Darüber hinaus können Sie Beispiele sehen und mit gelösten koplanaren Punkten üben.
Was sind koplanare Punkte?
In der analytischen Geometrie haben koplanare (oder koplanare) Punkte folgende Bedeutung:
Koplanare Punkte sind Punkte, die zur gleichen Ebene gehören.
Daher sind 2 oder 3 Punkte immer koplanar, da eine Ebene bereits mit 3 Punkten gebildet werden kann. Wenn andererseits 4, 5 oder mehr Punkte vorhanden sind, ist es möglich, dass einige der Punkte nicht in derselben Ebene liegen und daher nicht koplanar sind.
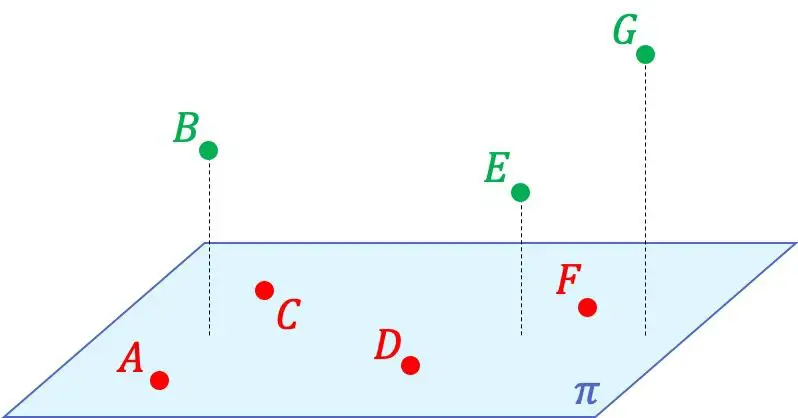
In der obigen grafischen Darstellung können Sie beispielsweise sehen, dass die Punkte A, C, D und F koplanar zueinander sind, da sie in derselben Ebene liegen. Andererseits sind diese 4 Punkte nicht koplanar mit den Punkten B, E und G, da in dem Raum, der alle Punkte enthält, keine Ebene gebildet werden kann.
Aus dieser Eigenschaft können wir ableiten, dass die durch koplanare Punkte definierten Vektoren auch koplanare Vektoren sind, das heißt, sie liegen in derselben Ebene.
Wann sind Punkte koplanar?
Wie wir bei der Definition koplanarer (oder koplanarer) Punkte gesehen haben, sind zwei oder drei Punkte immer koplanar, aber mehr als drei Punkte müssen die Koplanaritätsbeziehung nicht respektieren.
Es gibt also hauptsächlich zwei Methoden, um zu bestimmen, ob vier oder mehr Punkte koplanar sind:
- Eine Möglichkeit herauszufinden, ob die Punkte koplanar sind, sind die Vektoren, die durch die Punkte bestimmt werden: Wenn diese Vektoren koplanar sind , dann sind auch die Punkte koplanar.
Um diese Methode anwenden zu können, müssen Sie natürlich wissen, wann die Vektoren koplanar sind. Da es aber auch mehrere Möglichkeiten gibt, festzustellen, ob eine Menge von Vektoren koplanar ist, empfehlen wir Ihnen, sich anzuschauen , wie Sie feststellen können, ob Vektoren koplanar sind . Hier finden Sie alle Verfahren, die es gibt, um herauszufinden, wann 2, 3, 4 oder mehr Vektoren koplanar sind, sowie Beispiele und gelöste Aufgaben.
- Eine andere Möglichkeit herauszufinden, ob eine Menge von Punkten koplanar ist, besteht darin , die Gleichung der Ebene zu finden , die durch drei Punkte in der Menge gebildet wird. Wenn die anderen Punkte diese Gleichung erfüllen, bedeutet dies, dass alle Punkte in der Menge koplanar sind.
Obwohl es vom Problem abhängt, empfehlen wir die Verwendung der ersten der beiden Methoden, da es viel einfacher und schneller ist, zu überprüfen, ob die Vektoren koplanar sind, als die Gleichung einer Ebene zu berechnen. Aber verwenden Sie natürlich das, was Sie bevorzugen.
Probleme mit koplanaren Punkten gelöst
Übung 1
Bestimmen Sie, ob die folgenden drei Punkte koplanar sind:
In diesem Fall ist es nicht notwendig, irgendwelche Berechnungen durchzuführen, da 3 Punkte immer koplanar sind , was auch immer sie sein mögen.
Übung 2
Bestimmen Sie, ob die folgenden vier Punkte koplanar sind:
Damit die vier Punkte koplanar sind, müssen die von ihnen bestimmten Vektoren koplanar sein. Wir berechnen daher diese Vektoren:
Konstruieren wir nun die aus den Vektoren gebildete Matrix:
![\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-873ec750665fdf215a648778d6fcf042_l3.png "Rendered by QuickLaTeX.com")
Damit die resultierenden Vektoren koplanar sind, muss der Rang der vorherigen Matrix gleich 2 sein. Und dafür muss die Determinante der gesamten 3×3-Matrix gleich Null sein:
![\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-3eadb62f19c07b8a646fe9b2a00f9003_l3.png "Rendered by QuickLaTeX.com")
Die Determinante der gesamten Matrix ist jedoch ungleich Null, sodass der Rang der Matrix 3 ist und die 4 Punkte daher nicht koplanar sind .
Übung 3
Finden Sie heraus, ob die folgenden fünf Punkte koplanar sind:
Damit alle fünf Punkte koplanar sind, müssen die durch sie definierten Vektoren koplanar sein. Wir berechnen daher diese Vektoren:
Konstruieren wir nun die aus den Vektoren zusammengesetzte Matrix:
![\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d571ea172dbf5e6b7d85da6db466eb0_l3.png "Rendered by QuickLaTeX.com")
Damit die resultierenden Vektoren koplanar sind, muss der Rang der vorherigen Matrix gleich 2 sein. Wir berechnen daher den Rang der Vektormatrix anhand von Determinanten, um zu überprüfen, ob sie koplanar sind:
![\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bec15883d9e3aa5a401afa41cd3992ae_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd2f8cfa577e91b74c69e50cc36dfd9a_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d551dddceb916cc6cf8bf4137903da1d_l3.png "Rendered by QuickLaTeX.com")
Der Rang der Matrix entspricht 2, die Vektoren sind also koplanar und daher sind auch die 5 Punkte koplanar.
Übung 4
Parameterwert berechnen
so dass die folgenden 4 Punkte koplanar sind:
Damit die vier Punkte koplanar sind, müssen die von ihnen bestimmten Vektoren koplanar sein. Wir berechnen daher diese Vektoren:
Dessen Vektormatrix ist:
![\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png "Rendered by QuickLaTeX.com")
Damit die resultierenden Vektoren koplanar sind, muss der Rang der Matrix 2 sein. Und daher muss die Determinante der gesamten 3×3-Matrix 0 sein:
![\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png "Rendered by QuickLaTeX.com")
Schließlich lösen wir das Unbekannte
Wenn dieser Artikel für Sie hilfreich war, interessiert Sie wahrscheinlich auch die Berechnung des Abstands zwischen zwei Punkten (Formel) , da wir bei analytischen Geometrieproblemen manchmal gefragt werden, wie groß der Abstand zwischen zwei Punkten ist. Auf der verlinkten Seite finden Sie eine sehr ausführliche Erklärung, sowie Beispiele und Schritt für Schritt gelöste Übungen.