Gemischtes Produkt aus drei Vektoren (oder Dreifachpunktprodukt)

Auf dieser Seite erklären wir, was das gemischte Produkt dreier Vektoren (oder Dreifachpunktprodukt) ist und wie es berechnet wird. Außerdem sehen Sie Beispiele, Übungen und gelöste Probleme zu dieser Art von Operation zwischen Vektoren. Darüber hinaus finden Sie die Eigenschaften und Anwendungen des Mischprodukts.

Was ist das gemischte Produkt dreier Vektoren?

Das gemischte Produkt dreier Vektoren, auch dreifaches Skalarprodukt genannt, ist eine sukzessive Multiplikation zwischen drei Vektoren, die zwei verschiedene Arten von Operationen umfasst: das Skalarprodukt und das Vektorprodukt . Die Kombination der beiden Vektoroperationen ergibt also einen Skalar (eine reelle Zahl).

Konkret besteht das gemischte Produkt aus der Berechnung des Vektorprodukts zweier Vektoren und der anschließenden vektoriellen Multiplikation des erhaltenen Ergebnisses mit einem dritten Vektor. So geschrieben mag es sehr kompliziert erscheinen, aber in Wirklichkeit ist es gar nicht so viel, schauen Sie sich die Formel des Triple-Dot-Produkts an:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})$

Wie Sie in der Formel sehen können, wird das gemischte Produkt dreier Vektoren durch zwei eckige Klammern angezeigt.

Wie berechnet man das gemischte Produkt dreier Vektoren?

Die Dreipunktproduktformel ist die, die wir gerade im vorherigen Abschnitt gesehen haben. Sie wird jedoch im Allgemeinen nicht zur Bestimmung des gemischten Produkts dreier Vektoren verwendet, da es einen anderen, einfacheren und schnelleren Weg gibt:

Es seien drei beliebige Vektoren:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)\qquad \vv{\text{w}}= (\text{w}_x,\text{w}_y,\text{w}_z)$

Um das gemischte Produkt zwischen drei Vektoren zu berechnen, lösen Sie einfach die 3×3-Determinante, die durch die Komponenten der Vektoren gebildet wird:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}$

Damit Sie ein Beispiel dafür sehen können, wie dies berechnet wird , finden wir das gemischte Produkt der folgenden drei Vektoren:

$\vv{\text{u}}= (1,2,0) \qquad \vv{\text{v}}= (0,-1,3)\qquad \vv{\text{w}}= (-2,4,1)$

Um das gemischte Produkt zu bestimmen, konstruieren wir eine Determinante der Ordnung 3, indem wir die Vektoren in Zeilen der Matrix platzieren:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

Und jetzt müssen wir nur noch die Determinante der Matrix lösen, dafür können Sie jede Methode verwenden. In diesem Fall wenden wir die Regel von Sarrus an (dies kann aber auch durch Additionen oder Cofaktoren erfolgen):

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}$

Um zu zeigen, dass die beiden Verfahren äquivalent sind, berechnen wir das Mischprodukt derselben Vektoren anhand ihrer Definition:

$\begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}$

Wir empfehlen, das Mischprodukt über die Determinante der Vektoren zu berechnen, da dies schneller ist und die Fehlerwahrscheinlichkeit geringer ist. Aber wie Sie sehen, ist das Ergebnis unabhängig von der verwendeten Methode das gleiche. Verwenden Sie also die Methode, die Ihnen am besten gefällt. 👍

Geometrische Interpretation des Mischprodukts

Sobald Sie wissen, wie man das gemischte Produkt von drei Vektoren findet, fragen Sie sich vielleicht … und wozu dient das gemischte Produkt? Nun, in der Mathematik hat es zwei Hauptverwendungszwecke: die Berechnung des Volumens eines Parallelepipeds und des Volumens eines Tetraeders.

Das Volumen eines Parallelepipeds ist gleich dem Absolutwert des gemischten Produkts der Vektoren, die die drei Dimensionen des geometrischen Feldes markieren.

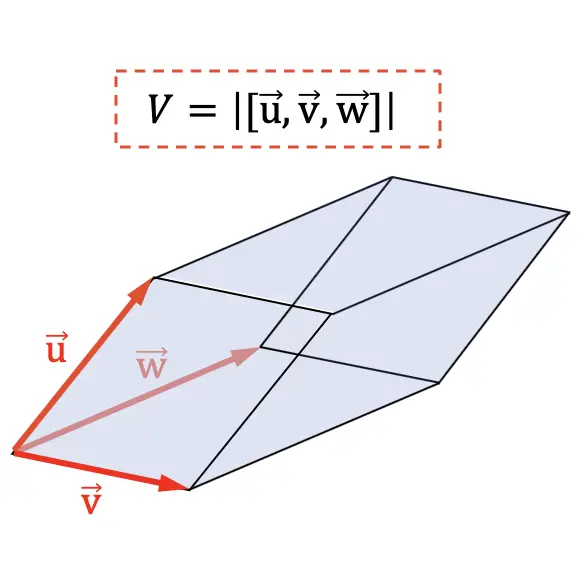
Beispiel eines gemischten Produkts aus drei Vektoren oder eines dreifachen Skalarprodukts

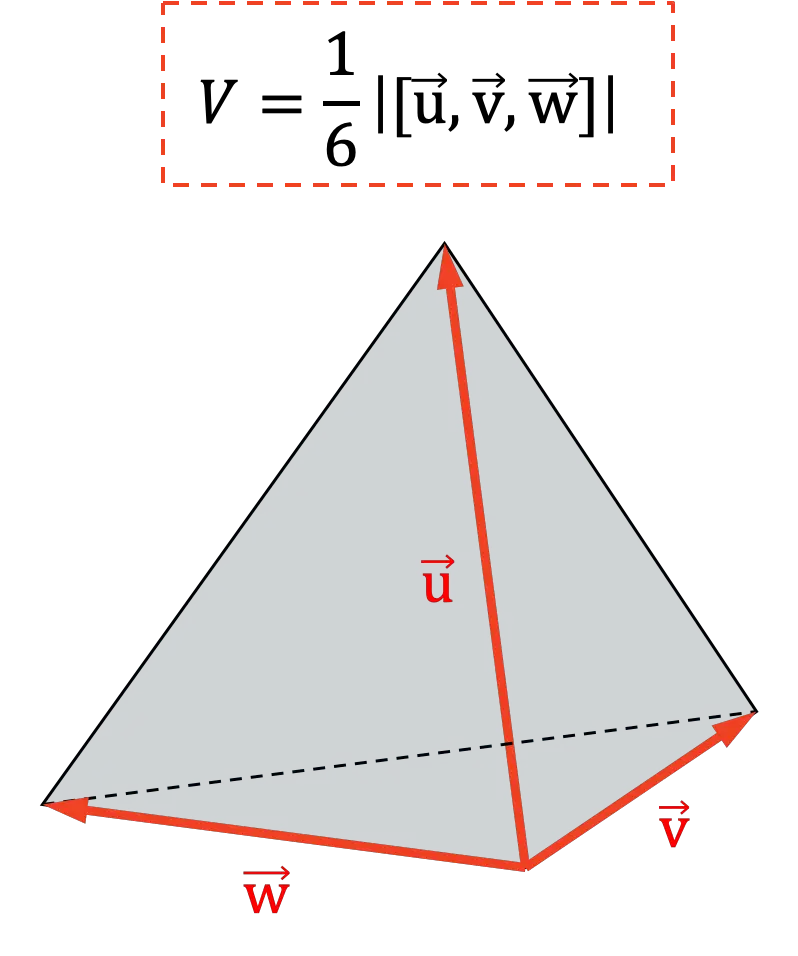
Eine weitere Anwendung des Mischprodukts ist die Bestimmung des Volumens eines Tetraeders . Da geometrisch gesehen der sechste Teil des Absolutwerts des Mischprodukts das Volumen eines Tetraeders darstellt:

gemischtes Produkt von drei Vektoren in r3

Eigenschaften des Mischprodukts bzw. Triple-Dot-Produkts

Das gemischte Produkt oder dreifache Skalarprodukt hat die folgenden Eigenschaften:

Im Allgemeinen bedeutet eine Änderung der Reihenfolge gemischter Produktvektoren auch einen Vorzeichenwechsel. Daher ist die Reihenfolge der gemischten Produktvektoren wichtig.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{v}},\vv{\text{u}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{u}},\vv{\text{w}},\vv{\text{v}}\bigr] = - \bigl[\vv{\text{w}},\vv{\text{v}},\vv{\text{u}}\bigr]$

Wenn wir jedoch die Reihenfolge zyklisch ändern, ändert sich das Vorzeichen nicht:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \bigl[\vv{\text{v}},\vv{\text{w}},\vv{\text{u}}\bigr] = \bigl[\vv{\text{w}},\vv{\text{u}},\vv{\text{v}}\bigr]$

In einem dreidimensionalen Raum (im R3) ist das gemischte Produkt von drei linear abhängigen oder koplanaren Vektoren (die zur gleichen Ebene gehören) gleich 0.

Probleme mit gemischten Produkten behoben

Übung 1

Gegeben sind 3 Vektoren:

$\vv{\text{u}}= (3,-1,2) \qquad \vv{\text{v}}= (-2,0,1)\qquad \vv{\text{w}}= (5,1,-1)$

Berechnen Sie das Mischprodukt der drei Vektoren:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

siehe Lösung

Um sein gemischtes Produkt zu finden, müssen wir die Determinante lösen, die sich aus den Koordinaten der Vektoren zusammensetzt:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}$

Übung 2

Gegeben sind 3 Vektoren:

$\vv{\text{u}}= (7,2,-3) \qquad \vv{\text{v}}= (2,4,9)\qquad \vv{\text{w}}= (4,3,-1)$

Bestimmen Sie das Mischprodukt zwischen den drei Vektoren:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

siehe Lösung

Um das gemischte Produkt zu finden, müssen wir nach der Determinante auflösen, die die kartesischen Koordinaten der Vektoren in Linienform hat:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}$

Übung 3

Berechnen Sie das Volumen des Parallelepipeds, dessen drei Seiten die folgenden Vektoren sind:

$\vv{\text{u}}= (0,2,5) \qquad \vv{\text{v}}= (-1,6,2)\qquad \vv{\text{w}}= (3,1,2)$

siehe Lösung

Das Volumen eines Parallelepipeds ist gleich dem Absolutwert des gemischten Produkts aus drei der Vektoren, die es als Kanten hat. Daher berechnen wir zunächst das dreifache Kreuzprodukt der Vektoren:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}$

Damit ist das Volumen des Parallelepipeds der Absolutwert des Ergebnisses des Mischprodukts:

$V= \lvert -79 \rvert = \bm{79}\ \mathbf{u}\bm{^3}$

Übung 4

Berechnen Sie das Volumen des Tetraeders, dessen Eckpunkte die folgenden Punkte sind:

$A(1,0,2) \qquad B(3,3,2)\qquad C(5,-1,4)\qquad D(4,2,1)$

siehe Lösung

Zuerst berechnen wir die Vektoren, die die Kanten des Tetraeders darstellen:

$\vv{AB}=B-A= (3,3,2)-(1,0,2)=(2,3,0)$

$\vv{AC}=C-A= (5,-1,4)-(1,0,2)=(4,-1,2)$

$\vv{AD}=D-A= (4,2,1)-(1,0,2)=(3,2,-1)$

Das Volumen eines Tetraeders entspricht einem Sechstel des Absolutwerts des gemischten Produkts aus drei seiner Vektoren für die Kanten. Daher berechnen wir zunächst das Mischprodukt der gefundenen Vektoren:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}$

Somit beträgt das Volumen des Tetraeders ein Sechstel des Absolutwerts des Mischprodukts:

$V= \cfrac{1}{6} \cdot \lvert 24 \rvert = \cfrac{24}{6} = \bm{4} \ \mathbf{u}\bm{^3}$

Gemischtes produkt aus drei vektoren (oder dreifachpunktprodukt)

Was ist das gemischte Produkt dreier Vektoren?

Wie berechnet man das gemischte Produkt dreier Vektoren?

Geometrische Interpretation des Mischprodukts

Eigenschaften des Mischprodukts bzw. Triple-Dot-Produkts

Probleme mit gemischten Produkten behoben

Übung 1

Übung 2

Übung 3

Übung 4

Kommentar verfassen Kommentieren abbrechen