▷ Woher weiß ich, ob 3 (oder mehr) Punkte ausgerichtet sind? ✅

Auf dieser Seite finden Sie die Erklärung, was ausgerichtete Punkte sind. Außerdem sehen Sie alle verfügbaren Methoden, um festzustellen, ob 3 (oder mehr) Punkte ausgerichtet sind. Darüber hinaus finden Sie zahlreiche Beispiele und sogar gelöste Übungen zum Üben.

Was bedeutet es, dass die Punkte ausgerichtet sind?

In der analytischen Geometrie werden drei oder mehr Punkte ausgerichtet, wenn sie alle auf derselben Linie liegen, das heißt, wenn sie durch Zeichnen einer geraden Linie zwischen ihnen verbunden werden können.

Offensichtlich werden immer zwei Punkte ausgerichtet, da Sie immer eine Linie zwischen zwei Punkten ziehen können. Allerdings müssen drei Punkte nicht auf derselben Linie liegen. Es gibt im Wesentlichen zwei Methoden, um festzustellen, ob drei oder mehr Punkte ausgerichtet sind:

Vektormethode : besteht darin, zu prüfen, ob die Vektoren, die die Punkte bilden, proportional sind.
Liniengleichungsmethode : Sie besteht darin, zu bestimmen, ob die Punkte zur gleichen Linie gehören.

Nachfolgend finden Sie Erläuterungen zu den einzelnen Verfahren und Beispiele, damit Sie entscheiden können, welches für Sie am besten geeignet ist.

So erkennen Sie, ob 3 (oder mehr) Punkte mit der Vektormethode ausgerichtet sind

Unter Berücksichtigung von drei Punkten:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Die drei Punkte werden ausgerichtet, wenn die Vektoren

$\vv{AB}$

Und

$\vv{BC}$

sie haben die gleiche Richtung, das heißt, wenn ihre Komponenten proportional sind.

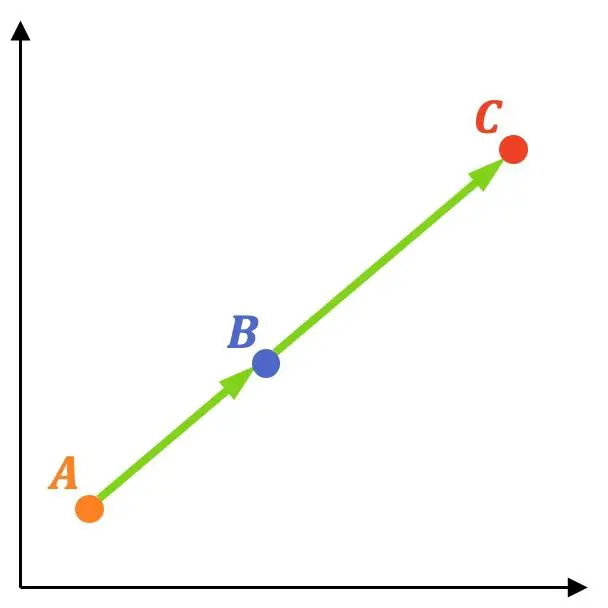
Punkte, die in einer Ebene ausgerichtet sind

Sehen wir uns ein Beispiel dafür an:

Stellen Sie fest, ob die folgenden drei Punkte übereinstimmen:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

Zuerst berechnen wir die Vektoren zwischen den Punkten. Es reicht aus, zwei verschiedene Vektoren zu berechnen:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

Und dann prüfen wir, ob die Koordinaten der Vektoren proportional sind:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

Durch Division der X-Komponenten und der Y-Komponenten der beiden Vektoren erhalten wir das gleiche Ergebnis (-2), daher haben die Vektoren die gleiche Richtung und daher sind die Punkte ausgerichtet .

Diese Methode kann auch verwendet werden, um herauszufinden, ob drei oder mehr Punkte im Raum (in R3) ausgerichtet sind. Es muss lediglich überprüft werden, ob die dritte Komponente der beiden Vektoren (Z-Komponente) ebenfalls proportional ist.

Wenn dieser Artikel für Sie nützlich ist, wird es Sie wahrscheinlich auch interessieren, wie man den Mittelpunkt zwischen zwei Punkten berechnet, da das Ermitteln des Mittelpunkts zweier Punkte offensichtlich eine Möglichkeit ist, einen dritten Punkt zu bestimmen, der mit den anderen beiden Punkten ausgerichtet ist. Wie es geht, können Sie auf der verlinkten Seite sehen, außerdem können Sie dort auch Beispiele und Schritt für Schritt gelöste Übungen sehen.

So erkennen Sie, ob 3 (oder mehr) Punkte mit der Geradengleichungsmethode ausgerichtet sind

Wie wir gerade im vorherigen Abschnitt gesehen haben, besteht eine Möglichkeit, die Ausrichtung von drei oder mehr Punkten zu untersuchen, darin, die Vektoren zu verwenden, die sich zwischen ihnen bilden können. Nun, eine andere Methode besteht darin, mit der Gleichung einer Geraden zu beginnen:

Unter Berücksichtigung von drei Punkten:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Die drei Punkte sind ausgerichtet, wenn sie alle zur gleichen Linie gehören. Um festzustellen, ob drei oder mehr Punkte ausgerichtet sind, müssen daher die folgenden Schritte ausgeführt werden:

Finden Sie die Gleichung der Geraden, die durch zwei der drei Punkte verläuft.
Prüfen Sie, ob der dritte Punkt auch zur Linie gehört. In diesem Fall bedeutet dies, dass die drei Punkte ausgerichtet sind. Wenn die Bedingung jedoch nicht erfüllt ist, bedeutet dies, dass die Punkte nicht ausgerichtet sind.

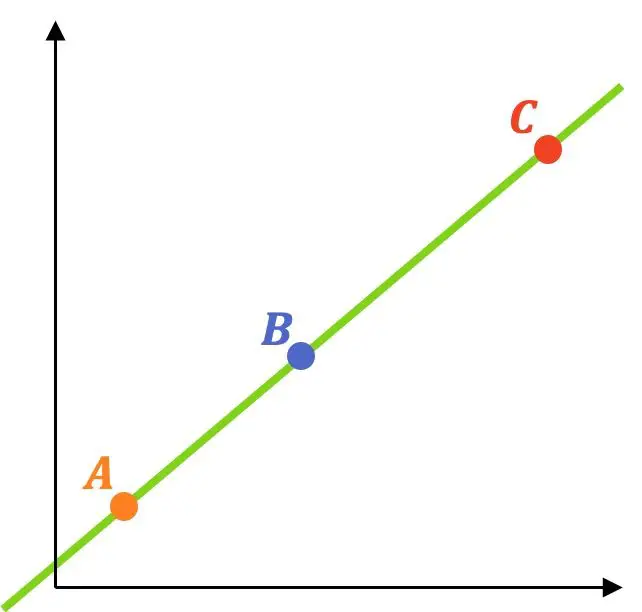
Als Beispiel lösen wir eine Übung mit dieser Methode:

Überprüfen Sie, ob die folgenden 3 Punkte übereinstimmen:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Zunächst müssen wir die Gleichung der Geraden berechnen, die durch die Punkte A und B verläuft. Wir ermitteln also den Richtungsvektor der Geraden:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Jetzt müssen Sie die Geradengleichung konstruieren. Sie können den gewünschten Typ auswählen: parametrisch, implizit, allgemein usw. Aber in diesem Fall werden wir die kontinuierliche Gleichung verwenden. Die stetige Gleichung der Geraden, die durch Punkt A und Punkt B verläuft, lautet also:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Sobald wir die Gleichung der Geraden haben, müssen wir prüfen, ob der andere Punkt auch zur gleichen Geraden gehört. Dazu setzen wir die Koordinaten des Punktes C in die Geradengleichung ein:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

Wir haben einen Gleichstand, also erfüllt der Punkt die Geradengleichung. Und deshalb sind die 3 Punkte kollinear .

Es ist zu beachten, dass eine Menge ausgerichteter Punkte nicht den gleichen Abstand haben muss, d. h. der Abstand zwischen mehreren ausgerichteten Punkten kann unterschiedlich sein. Den Unterschied zwischen den beiden Konzepten erkennen Sie an der Erklärung des Abstands zwischen zwei Punkten (Geometrie) , wo Sie auch Beispiele und Schritt für Schritt gelöste Übungen sehen können.

Übungen zu ausgerichteten Punkten gelöst

Übung 1

Stellen Sie fest, ob die folgenden drei Punkte übereinstimmen:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Sehen Sie sich die Lösung an

Wir können eine der beiden Methoden wählen, die wir gesehen haben, um das Problem zu lösen. In diesem Fall verwenden wir die Vektormethode.

Zuerst berechnen wir die Vektoren zwischen den Punkten:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

Und jetzt prüfen wir, ob die kartesischen Koordinaten der Vektoren proportional sind:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

Indem wir die X-Komponenten und die Y-Komponenten der beiden Vektoren durcheinander dividieren, erhalten wir das gleiche Ergebnis (-4), sodass die Vektoren die gleiche Richtung haben. Tatsache, die darauf hinweist, dass die Punkte ausgerichtet sind .