Gleichungssysteme sind Mengen von zwei oder mehr Gleichungen, die mehr als eine Unbekannte haben. Um Systeme zu lösen, können wir also vier Methoden verwenden: Substitution, Entzerrung, Reduktion und grafische Darstellung. Bevor wir jedoch mit der Erläuterung der Lösungsverfahren beginnen, definieren wir die existierenden Systemtypen entsprechend der Anzahl der Lösungen:
- Bestimmtes kompatibles System: Es hat nur eine Lösung und kann durch zwei Linien dargestellt werden, die sich in einem einzigen Punkt (dem Lösungspunkt) schneiden.
- Unbestimmtes kompatibles System: Es hat unendlich viele Lösungen und das liegt daran, dass es zwei Geraden gibt, die an denselben Punkten zusammenfallen.
- Inkompatibles System: Es gibt keine Lösung, da die Geraden parallel sind und daher keinen gemeinsamen Punkt haben.
Methoden zur Lösung linearer Gleichungssysteme
Wir erklären nun die verschiedenen Systeme, mit denen wir Gleichungssysteme lösen können. In den Erläuterungen finden Sie die Theorie und einige Beispiele, dank derer alle erläuterten Konzepte klarer werden. Beachten Sie, dass wir in diesem Artikel nur über Systeme mit 2×2-Gleichungen sprechen, was bedeutet, dass wir uns lediglich mit Systemen befassen, die aus zwei Gleichungen bestehen. Beginnen wir jedoch mit der Erklärung.
Substitutionsmethode
Die Substitutionsmethode besteht darin, eine der Unbekannten in einer der Gleichungen zu isolieren und dann den erhaltenen Ausdruck in die entgegengesetzte Gleichung einzusetzen. Diese Methode wird am meisten empfohlen, wenn mindestens eine der Unbekannten den Koeffizientenwert 1 hat. Daher sind die folgenden Schritte sehr einfach:
- Isolieren Sie eine unbekannte Größe aus einer der beiden Gleichungen.
- Setzen Sie in die andere Gleichung den Ausdruck ein, der der Unbekannten entspricht, die wir aus der ersten Gleichung entfernt haben.
- Löschen Sie die entgegengesetzte Unbekannte in der Gleichung, die wir erhalten haben.
- Sobald wir den Wert der ersten Variablen haben, müssen wir ihn verwenden, um die zweite zu finden.
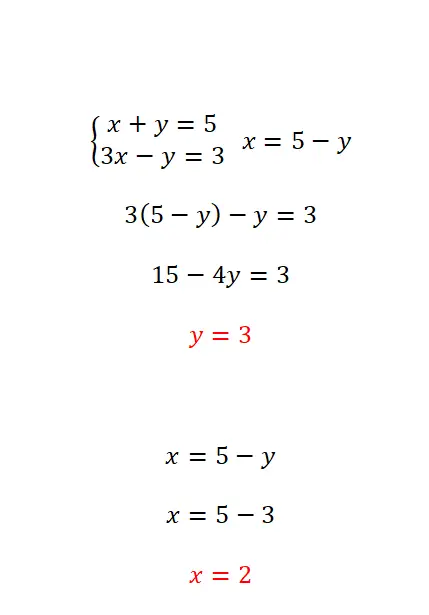
Ausgleichsmethode
Die Matching-Methode besteht darin, dieselbe Variable in den beiden Gleichungen zu isolieren und dann die beiden erhaltenen Ausdrücke abzugleichen. Diese Methode wird empfohlen, wenn dieselbe Unbekannte in beiden Gleichungen leicht isoliert werden kann, da sie die gesamte Berechnung vereinfacht. In diesem Fall müssen Sie wie folgt vorgehen:
- Wir isolieren die von uns gewählte Unbekannte in den beiden Gleichungen.
- Wir assimilieren die äquivalenten Ausdrücke zu dieser Unbekannten.
- Wir lösen die Gleichung normal.
- Wir berechnen die andere Unbekannte mit dem von uns berechneten Wert.
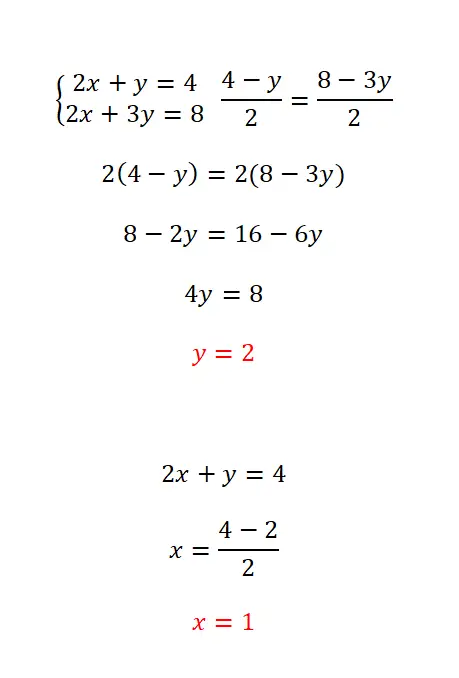
Reduktionsmethode
Die Reduktionsmethode basiert auf der Multiplikation beider Gleichungen mit zwei Zahlen, wodurch wir in beiden Ausdrücken denselben Koeffizienten mit unterschiedlichem Vorzeichen einer der Variablen erhalten. Diese Methode wird am meisten empfohlen, wenn die gleiche Unbekannte in allen Gleichungen den gleichen Koeffizienten hat oder wenn die gleichen Koeffizienten entgegengesetzte Vorzeichen haben. Und das Auflösungsverfahren ist wie folgt:
- Die beiden Gleichungen werden mit den erforderlichen Zahlen multipliziert (Sie müssen zwei Zahlen finden, die es ermöglichen, für eine der beiden Variablen in den beiden Gleichungen denselben Koeffizienten, jedoch mit entgegengesetztem Vorzeichen, zu erhalten).
- Dann werden die Gleichungen subtrahiert oder addiert, um diese Unbekannte mit ihren jeweiligen Koeffizienten zu eliminieren.
- Dann wird die verbleibende Gleichung gelöst.
- Und wir verwenden das Ergebnis dieser Gleichung, um den numerischen Wert zu erhalten, der uns in der anderen Variablen fehlt.
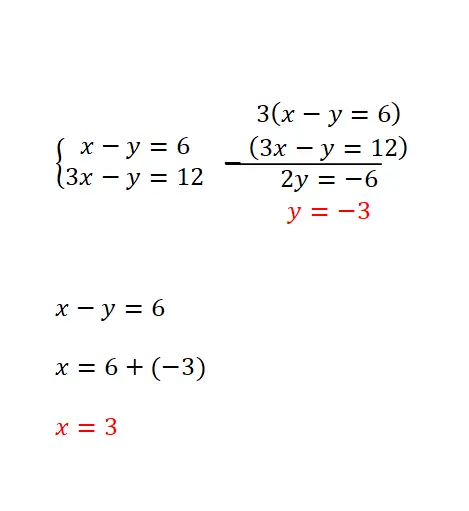
grafische Methode
Schließlich können wir uns dafür entscheiden, ein Gleichungssystem mithilfe einer grafischen Darstellung zu lösen. Diese Methode unterscheidet sich erheblich von den anderen, da sie keinen komplexen mathematischen Teil enthält und fast ausschließlich grafisch ist. Um also die Werte der Unbekannten zu kennen, müssen wir die beiden Gleichungen in Form der Geradengleichung strukturieren: y = mx + b . Auf diese Weise können wir die Darstellung erstellen und dann die Werte der Koordinaten des Schnittpunkts zwischen den beiden Funktionen mit den Unbekannten verknüpfen. Hier ist ein ausgearbeitetes Beispiel:
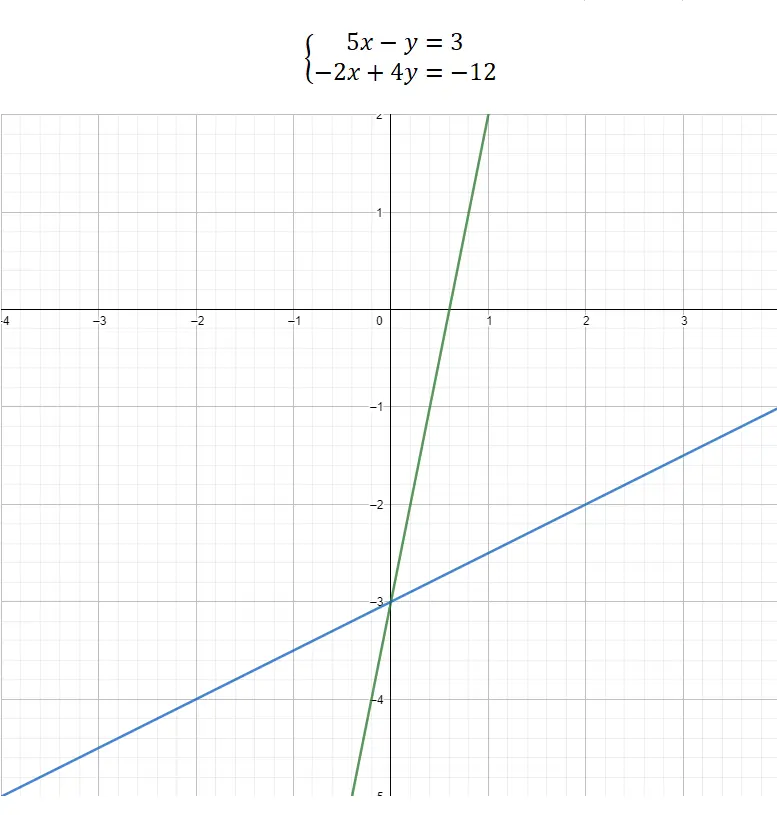
Wie in der Grafik zu sehen ist, liegt der Grenzwert zwischen den beiden Funktionen bei (0, -3). Daher ist der Wert von x = 0 und der Wert von y = -3. So wird ein Gleichungssystem grafisch gelöst.
Wie löst man ein System quadratischer Gleichungen?
Um Systeme quadratischer Gleichungen zu lösen, können wir die gerade besprochenen Methoden verwenden. Persönlich empfehlen wir gerne die Substitutionsmethode, da wir damit schnell eine Gleichung mit einer einzigen Unbekannten erhalten können. Wenn wir hingegen die Reduktions- oder Ausgleichsmethoden verwenden, wird die Berechnung ziemlich kompliziert. Sobald Sie also eine der beiden Variablen ersetzen, müssen Sie nur noch die resultierende quadratische Gleichung oder quadratische Gleichung lösen. Hier ist ein Beispiel, damit Sie den gesamten Prozess sehen können:
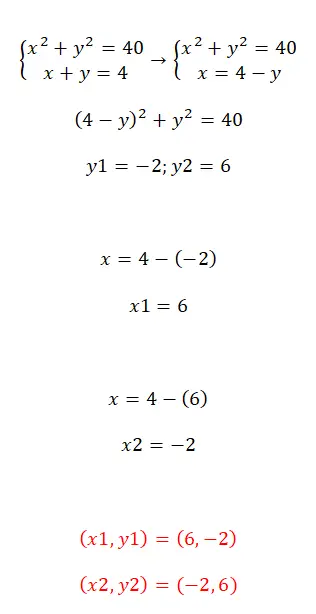
Übungen zum Lösen von Gleichungssystemen
Damit Sie die erläuterte Theorie anwenden können, bieten wir Ihnen nun einige Übungen zu Systemen linearer und quadratischer Gleichungen an. Auf diese Weise werden Sie alle Konzepte im Zusammenhang mit der Berechnung von Gleichungssystemen besser verstehen. Wir empfehlen, dass Sie versuchen, sie zu lösen, bevor Sie sich die von uns angebotenen Antworten ansehen. Auf diese Weise können Sie die Übungen optimal nutzen:
Übung 1
Lösen Sie dieses Gleichungssystem mit der Substitutionsmethode:
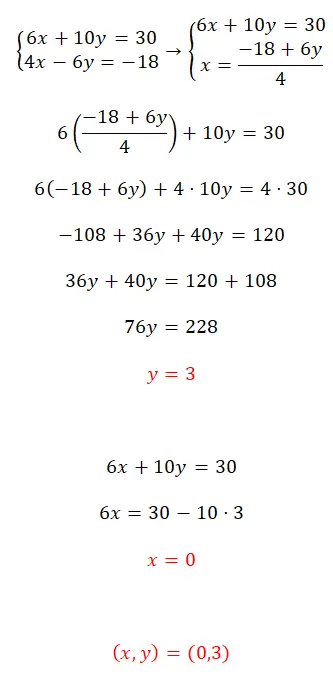
- Wir beginnen damit, eine der beiden Unbekannten in einer Gleichung zu isolieren.
- Dann ersetzen wir den in der entgegengesetzten Gleichung erhaltenen Ausdruck durch die Unbekannte, die wir zuvor gelöst haben.
- Wir erhalten dann das Ergebnis der entgegengesetzten Variablen.
- Als nächstes setzen wir den ersten entdeckten Wert in eine der beiden Gleichungen ein, um den Wert der ersten Unbekannten zu berechnen.
- Abschließend drücken wir das Ergebnis der beiden Variablen aus.
Übung 2
Lösen Sie dieses Gleichungssystem mit der Substitutionsmethode:
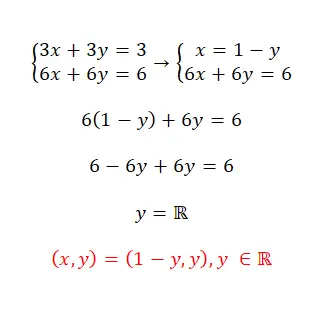
- In diesem Fall gehen wir genauso vor: Isolieren Sie eine Unbekannte, ersetzen Sie sie im anderen Ausdruck und isolieren Sie die zweite Variable.
- Wie wir sehen, handelt es sich um ein unbestimmt kompatibles System, da es unendlich viele Lösungen hat.
Übung 3
Lösen Sie dieses Gleichungssystem mit der Ausgleichsmethode:
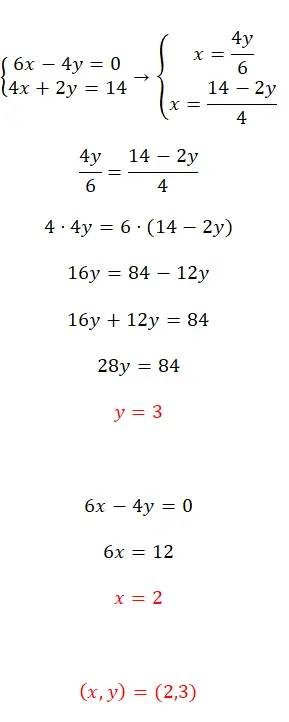
- Der erste Schritt besteht darin, in beiden Gleichungen dieselbe Variable zu isolieren, in diesem Fall haben wir x gewählt.
- Dann gleichen wir die resultierenden Ausdrücke ab und beginnen mit der Lösung.
- Somit erhalten wir den Wert der ersten Unbekannten.
- Und wenn wir es in eine der beiden ursprünglichen Gleichungen einsetzen, können wir die zweite Unbekannte berechnen.
- Abschließend drücken wir das Ergebnis der beiden Variablen aus.
Übung 4
Lösen Sie dieses Gleichungssystem mit der Ausgleichsmethode:
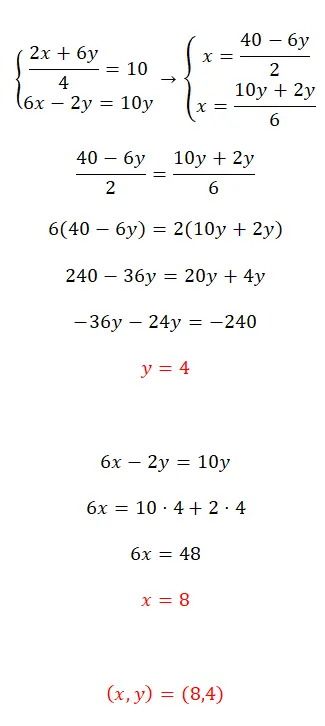
- Zuerst isolieren wir das x in beiden Gleichungen.
- Als nächstes gleichen wir die erhaltenen Ausdrücke ab.
- Wir erhalten den Wert der ersten Unbekannten.
- Wir setzen diesen Wert in eine der beiden Anfangsgleichungen ein und berechnen die zweite Unbekannte.
- Abschließend bringen wir den Wert der beiden Fremden zum Ausdruck.
Übung 5
Lösen Sie dieses Gleichungssystem mit der Reduktionsmethode:
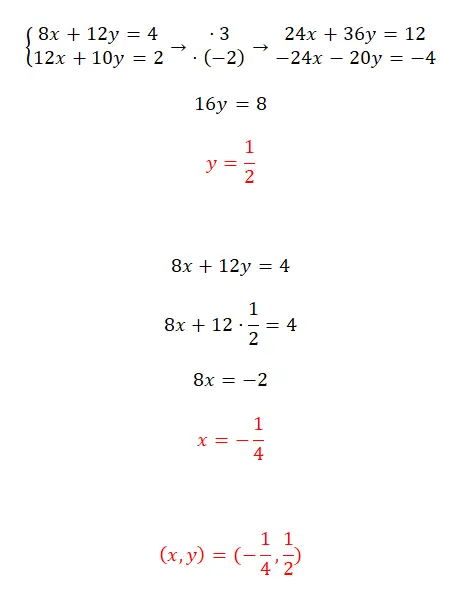
- Sie müssen nach zwei Zahlen suchen, die es ermöglichen, für eine der beiden Variablen in den beiden Gleichungen den gleichen Koeffizienten zu erhalten, jedoch mit entgegengesetztem Vorzeichen .
- Lösen Sie dann einfach die Gleichung, die wir durch Addition der beiden erhaltenen Ausdrücke erhalten.
- Als nächstes setzen wir y in eine der beiden ursprünglichen Gleichungen ein, um x zu berechnen.
- Abschließend drücken wir das Ergebnis des Systems aus.
Übung 6
Lösen Sie dieses Gleichungssystem mit der Reduktionsmethode:
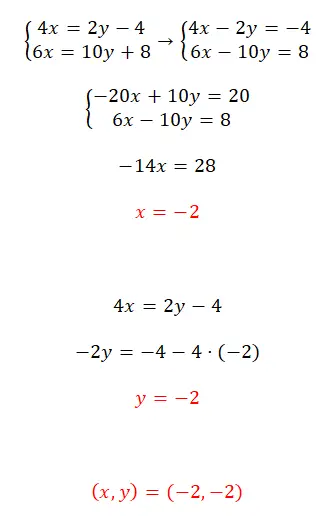
- Wir beginnen mit der Anordnung der Gleichungen (übergeben aller Variablen nach links).
- Dann multiplizieren wir die erste Gleichung mit -5.
- Wir lösen die Gleichung, die wir durch Addition der beiden Gleichungen erhalten, und erhalten den Wert von x.
- Wir verwenden diesen bekannten Wert, um den Wert von y zu erhalten.
- Wir drücken das Ergebnis des Gleichungssystems aus.
Übung 7
Lösen Sie dieses Gleichungssystem mit der Substitutionsmethode:
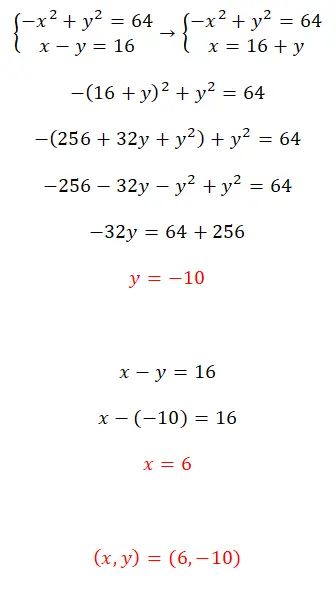
- Um dieses System nichtlinearer Gleichungen zu lösen, empfehlen wir die Verwendung der Substitutionsmethode.
- Sie konstruieren also eine Gleichung mit dem Ausdruck, der x entspricht.
- Sie erhalten den Wert des unbekannten y.
- Sie berechnen den Wert von x mit dem zuvor berechneten Wert.
- Und Sie haben bereits beide Werte.
Übung 8
Lösen Sie dieses Gleichungssystem mit der Methode Ihrer Wahl:
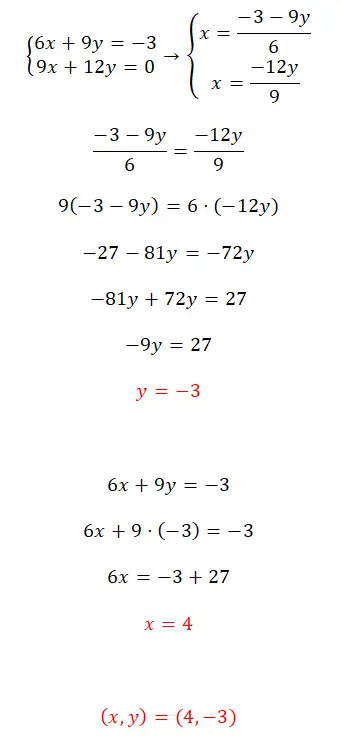
- In diesem Fall liegt uns ein ermitteltes kompatibles System vor und wir werden es mit der Ausgleichsmethode lösen.
- Deshalb lösen wir in beiden Gleichungen nach x auf und setzen die beiden resultierenden Ausdrücke gleich.
- Nachdem wir die Gleichung gelöst haben, erhalten wir den Wert von y.
- Wir verwenden diesen Wert, um den Wert von x zu ermitteln.
- Abschließend drücken wir das Ergebnis des Systems aus.