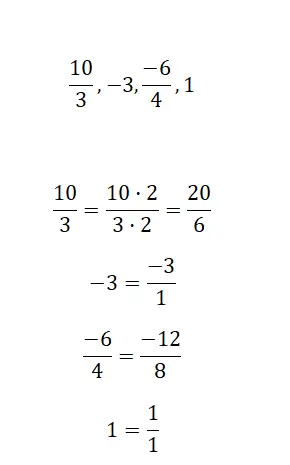In diesem Artikel finden Sie eine Erklärung zu äquivalenten Brüchen oder gleichen Brüchen, die sehr vollständig und leicht verständlich ist. Genauer gesagt werden wir über ihre Definition sprechen, wie man sie berechnet und wie man erkennt, ob zwei Brüche äquivalent sind. Auf diese Weise wissen Sie am Ende alles, was Sie zum Lösen von Übungen zu äquivalenten Brüchen benötigen, wie wir sie Ihnen am Ende vorstellen werden. Beginnen wir also mit dem Thema.
Rechner für äquivalente Brüche
Mit Hilfe dieses Rechners für äquivalente Brüche können Sie überprüfen, ob zwei Brüche gleich sind, ohne irgendwelche Berechnungen durchführen zu müssen. Die Bedienung ist sehr einfach, im Grunde müssen Sie die Werte eingeben, die den beiden Zählern und den beiden Nennern entsprechen, und auf die Schaltfläche „Berechnen“ klicken.
Was sind äquivalente Brüche?
Äquivalente Brüche sind solche, die denselben numerischen Wert ausdrücken . Daher sind sie Brüche, die demselben Ergebnis entsprechen, auch wenn sie einen unterschiedlichen Zähler und Nenner haben. Dies bedeutet, dass zwischen ihnen eine proportionale Beziehung besteht, die zweierlei Art sein kann: verstärkt oder vereinfacht. Als nächstes zeigen wir Ihnen ein grafisches Beispiel für äquivalente Brüche, damit das Konzept besser verstanden wird.
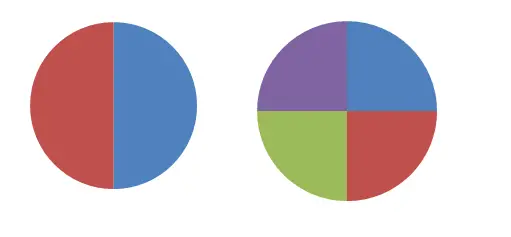
Im vorherigen Bild sehen Sie zwei Kreise, die in zwei und vier Teile unterteilt sind. Wenn wir versuchen, die erste durch einen Bruch zu definieren, sagen wir, dass jeder Teil gleich der Hälfte des Ganzen ist, während wir in der zweiten Zahl den Bruch 1/4 verwenden. Offensichtlich sind diese beiden Brüche nicht äquivalent , da sie unterschiedliche Größen darstellen. Wenn wir jedoch zwei Teile des zweiten Kreises (2/4) nehmen, entspricht dieser Ausdruck 1/2.
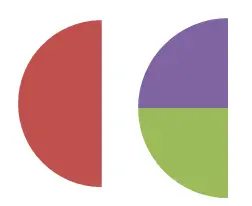
In diesem zweiten Bild sehen Sie die Äquivalenz zwischen 1/2 und 2/4 , sie kann auch numerisch überprüft werden. Da 1/2 = 0,5 und 2/4 = 0,5. Gemäß der Definition, die wir zuvor kommentiert haben, sind die beiden Brüche äquivalente Brüche, wenn sie denselben numerischen Wert ausdrücken.
Beispiele für äquivalente Brüche
Wir zeigen Ihnen nun 5 Beispiele für äquivalente Brüche. Und wenn Sie verstehen möchten, wie wir sie berechnet haben, empfehlen wir Ihnen, weiterzulesen.
- Brüche, die einer Hälfte entsprechen: 2/4, 3/6, 4/8 usw.
- Brüche, die einer Terz entsprechen: 2/6, 3/9, 4/12 usw.
- Brüche, die einem Viertel entsprechen: 2/8, 3/12, 4/16 usw.
- Brüche gleich Eins: 4/4, 7/7, 15/15 usw.
- Brüche, die einer Quinte entsprechen: 2/10, 3/15, 4/20 usw.
Wie berechnet man äquivalente Brüche?
Um äquivalente Brüche zu erhalten, müssen wir Zähler und Nenner mit derselben Zahl multiplizieren oder dividieren . Denn wenn wir beide Teile des Bruchs auf die gleiche Weise modifizieren, behalten wir eine proportionale Beziehung bei. Daher können wir zwei Methoden verwenden: Verstärkung und Reduktion.
Finden eines äquivalenten Bruchs durch Verstärkung
Im ersten Fall müssen wir einen Anfangsbruch mit einem bestimmten Zahlenwert multiplizieren. Das bedeutet, dass wir Zähler und Nenner mit dieser Zahl multiplizieren müssen. Damit Sie es an einem Beispiel sehen können, zeigen wir Ihnen im Folgenden zwei äquivalente Brüche, die sich nach einer Multiplikation ergeben:
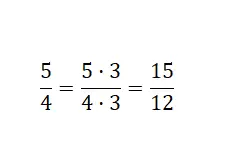
Wir haben beide Teile des Bruchs mit drei multipliziert: 5 x 3 = 15 und 4 x 3 = 12 . Wir erhalten somit einen verstärkten äquivalenten Bruchteil, da dieser größer ist. Zusammenfassend haben wir einen Bruch gefunden, der aus verschiedenen Zahlenwerten besteht und die gleiche Menge ausdrückt wie der ursprüngliche Bruch.
Finden eines äquivalenten Bruchs durch Vereinfachung
Zweitens können wir einen Bruch vereinfachen , indem wir Zähler und Nenner eines bestimmten Bruchs dividieren. Auf diese Weise erhalten wir einen weiteren äquivalenten Bruch , der noch einfacher als der erste ist. Es ist jedoch erwähnenswert, dass diese Methode nur funktioniert, wenn der anfängliche Ausdruck kein irreduzibler Bruch ist, da dieser nicht weiter reduziert werden kann. Nachfolgend finden Sie ein Beispiel für die Berechnung eines äquivalenten Bruchs durch Reduktion (Vereinfachung).
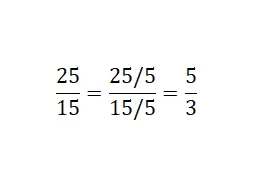
Wie Sie auf dem Bild sehen können, haben wir sowohl den Zähler als auch den Nenner des Bruchs durch einen gemeinsamen Teiler dividiert. In diesem Beispiel haben wir fünf verwendet: 25/5 = 5 und 15/5 = 3. Schließlich haben wir den irreduziblen äquivalenten Bruch von 25/15 erhalten.
Woher wissen Sie, ob zwei Brüche gleichwertig sind?
Um äquivalente Brüche zu identifizieren, müssen wir eines von drei Verfahren befolgen, die wir im Folgenden erläutern. Es sollte beachtet werden, dass die zweite mit der Vereinfachung von Brüchen zusammenhängt, über die wir im vorherigen Abschnitt gesprochen haben.
Zähler mit Nennern multiplizieren
Wenn Sie die Äquivalenz zwischen zwei Brüchen überprüfen möchten, können Sie dieses erste Verfahren verwenden. Grundsätzlich müssen Sie den Zähler des ersten Bruchs mit dem Nenner des zweiten multiplizieren. Als nächstes müssen Sie den Zähler des zweiten Bruchs mit dem Nenner des ersten multiplizieren. Wenn beide Ergebnisse dasselbe ergeben , sind diese Brüche gleichwertig. Schauen Sie sich das folgende Beispiel an:
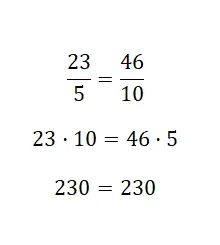
In diesem letzten Beispiel haben wir überprüft, dass die beiden Brüche äquivalent sind. Dieses Beispiel war leicht zu erkennen, da der zweite Bruch doppelt so groß ist wie der erste, d. h. sie haben eine verstärkte Äquivalenzbeziehung . Es ist zu beachten, dass dieses Verfahren recht komfortabel anzuwenden ist. Es reicht aus, nur die Kreuze zu multiplizieren. Wir empfehlen Ihnen aber auch, den Umgang mit den anderen beiden Systemen zu erlernen, da Ihnen dadurch mehr mathematische Ressourcen zur Verfügung stehen.
Brüche vereinfachen
Wenn es um nicht irreduzible Brüche geht, können wir diese andere Methode verwenden, die darin besteht, den aus den größten Zahlen bestehenden Bruch so weit wie möglich zu reduzieren. Wenn wir bei dieser Reduktion feststellen, dass der kleinere Bruch irreduzibel vom anderen ist, können wir davon ausgehen, dass sie äquivalent sind.
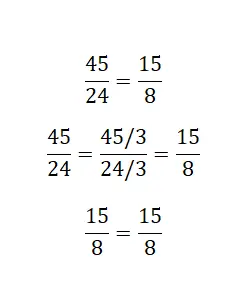
Spaltungen auflösen und ausgleichen
Schließlich können Sie auf die durch Brüche erzeugte Quotientenlösung zurückgreifen, da eine gemischte Zahl immer eine Division ist. Grundsätzlich müssen Sie den äquivalenten numerischen Wert der beiden Brüche berechnen. Wenn es sich um dieselbe Zahl handelt, sind sie äquivalent. Im folgenden Bild sehen Sie ein sehr anschauliches Beispiel:
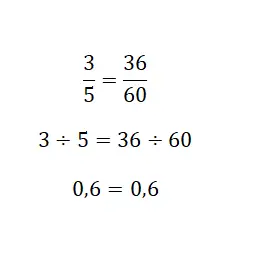
Übungen zu äquivalenten Brüchen
Nachdem Sie nun die gesamte Theorie gelesen haben, können Sie versuchen, die folgenden Übungen zu lösen, um die Erklärung vollständig zu verstehen. Wir empfehlen Ihnen, zu versuchen, sie selbst zu lösen, und sobald Sie sie haben, vergleichen Sie Ihr Ergebnis mit dem, das wir Ihnen anbieten. Das heißt, wir lassen Sie üben:
Übung 1
Finden Sie durch Vereinfachung einen äquivalenten Bruch für jeden von uns angebotenen Bruch:
Um diese Aufgabe zu lösen, wenden Sie einfach die Vereinfachung von Brüchen an und erhalten so den äquivalenten irreduziblen Bruch. Die vier Beispiele sind sehr ähnlich, sodass ihre Lösung keine großen Schwierigkeiten bereitet.
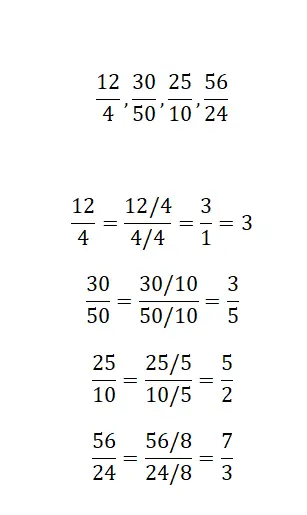
Übung 2
Finden Sie durch Verstärkung einen äquivalenten Bruch für jeden von uns vorgeschlagenen Bruch:
Als nächstes müssen Sie die von uns vorgeschlagenen Brüche verstärken, um so größere äquivalente Brüche zu erhalten. Es spielt keine Rolle, welche Zahl Sie für die Multiplikationen verwenden. Wir machen es beispielsweise mit 2 und 3.
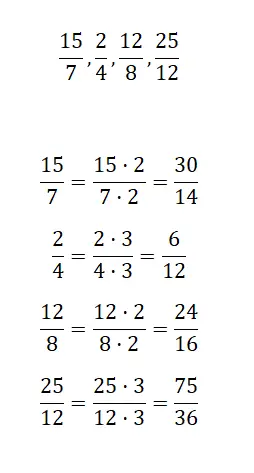
Übung 3
Bestimmen Sie, ob die folgenden Brüche äquivalent sind oder nicht:
Um herauszufinden, ob zwei Brüche äquivalent sind, müssen Sie eine der drei oben erläuterten Methoden verwenden. Sie werden feststellen, dass die Fehlerbehebungen durch das erste Verfahren gelöst wurden, es steht Ihnen jedoch frei, das gewünschte System zu verwenden.
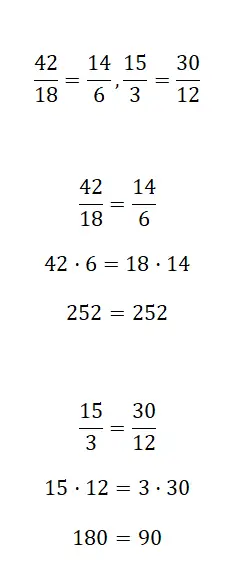
Übung 4
Berechnen Sie die äquivalenten Brüche der folgenden Ausdrücke:
In dieser letzten Übung müssen Sie die von uns vorgeschlagenen Ausdrücke ( ganze Zahlen und gemischte Zahlen) in Bruchform umschreiben und dabei versuchen, eine Äquivalenzbeziehung aufrechtzuerhalten.