Ähnliche Monome

Hier finden Sie die Erklärung, was ähnliche Monome sind. Darüber hinaus können Sie Beispiele für ähnliche Monome sehen und sogar mit gelösten Übungen zu dieser Art von Monomen üben.

Was sind ähnliche Monome?

Um die Bedeutung ähnlicher Monome zu verstehen, muss man natürlich zunächst wissen , was ein Monom ist . Ich empfehle Ihnen daher, einen Blick auf die verlinkte Seite zu werfen, bevor Sie fortfahren.

Dass also zwei Monome ähnlich sind, bedeutet Folgendes:

Ähnliche Monome sind Monome, die genau den gleichen Literalteil haben. Mit anderen Worten: Zwei oder mehr Monome sind ähnlich, wenn sie aus denselben Variablen (Buchstaben) und denselben Exponenten bestehen.

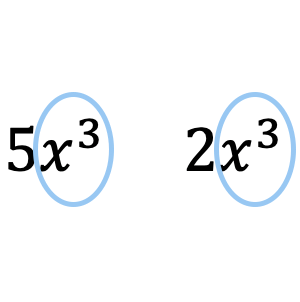
Wie Sie im obigen Beispiel sehen können, ist das Monom

$5x^3$

ist dem Monom ähnlich

$2x^3$

weil beide den gleichen wörtlichen Teil haben

$(x^3),$

auch wenn ihre Koeffizienten unterschiedlich sind.

Eines der Merkmale ähnlicher Monome ist, dass sie sowohl zum Addieren von Monomen als auch zum Subtrahieren von Monomen verwendet werden, zwei Operationen, die Sie mit Ja oder Ja beherrschen müssen. Klicken Sie auf einen der beiden Links, um zu sehen, wie man Monome addiert oder subtrahiert. Darüber hinaus finden Sie in jedem Link Beispiele und Schritt für Schritt gelöste Übungen.

Tatsächlich können Sie Monome nur addieren und subtrahieren, wenn sie ähnlich sind. Und genau deshalb sind ähnliche Monome in der Mathematik so wichtig.

Beispiele für ähnliche Monome

Damit Sie das Konzept ähnlicher Monome vollständig verstehen können, sehen Sie unten einige Beispiele für einander ähnliche Monome.

Beispiel 1

$4x^5 \qquad -2x^5$

Die beiden vorherigen Monome sind ähnlich, da ihre Literalteile äquivalent sind

$(x^5).$

Beispiel 2

$7xy^3 \qquad 8xy^3 \qquad -6xy^3$

Die vorherigen drei Monome sind ähnlich, weil ihre wörtlichen Teile gleich sind

$(xy^3).$

Beispiel 3

$12a^6b^2c^7 \qquad -4a^6b^2c^7$

$-5a^6b^2c^7 \qquad 1a^6b^2c^7$

Die vorherigen vier Monome sind einander ähnlich, da ihre wörtlichen Teile identisch sind

$(a^6b^2c^7).$

Übung ähnlicher Monome gelöst

Ordnen Sie Paare von Monomen zu, die ähnlich aussehen:

$\begin{array}{lcl} 4x^2 & \qquad \qquad & 2a^5x^6z \\[3ex]-3a^5x^6z & \qquad \qquad & 6x^2y^3z^6w^2 \\[3ex] 9y^3x & \qquad \qquad & 2xy^3 \\[3ex]4x^2y^3z^6w^2& \qquad \qquad & x^2 \end{array}$

siehe Lösung

Ähnliche Monome sind solche, die die gleichen wörtlichen Teile haben. Daher sind Paare ähnlicher Monome:

$4x^2 \quad \longleftrightarrow \quad x^2$

$-3a^5x^6z\quad \longleftrightarrow \quad 2a^5x^6z$

$9y^3x\quad \longleftrightarrow \quad 2xy^3$

$4x^2y^3z^6w^2\quad \longleftrightarrow \quad 6x^2y^3z^6w^2$

Obwohl es etwas völlig anderes bedeutet, sind Sie, wenn Sie es bis hierher geschafft haben, wahrscheinlich auch daran interessiert zu wissen, wie die Polynomzerlegung einer Zahl aussieht. Da dies etwas ist, von dem nur sehr wenige Menschen wissen, ist es tatsächlich sehr nützlich, um mathematische Ausdrücke zu vereinfachen.