Auf dieser Seite erfahren Sie, wie der Abstand zwischen zwei Linien im Raum berechnet wird (in R3), unabhängig von deren Typ (parallel, sekante, zusammenfallend, sekante, senkrechte Linien usw.). Darüber hinaus können Sie Beispiele und Übungen sehen, die Schritt für Schritt gelöst werden.
So berechnen Sie den Abstand zwischen zwei Linien
Der Abstand zwischen zwei Geraden ist der Mindestabstand zwischen jedem Punkt auf einer Geraden und jedem Punkt auf der anderen Geraden. Dieser Abstand entspricht der Länge des Segments, das von einer Linie zur anderen Linie geht und gleichzeitig senkrecht zu beiden Linien steht.
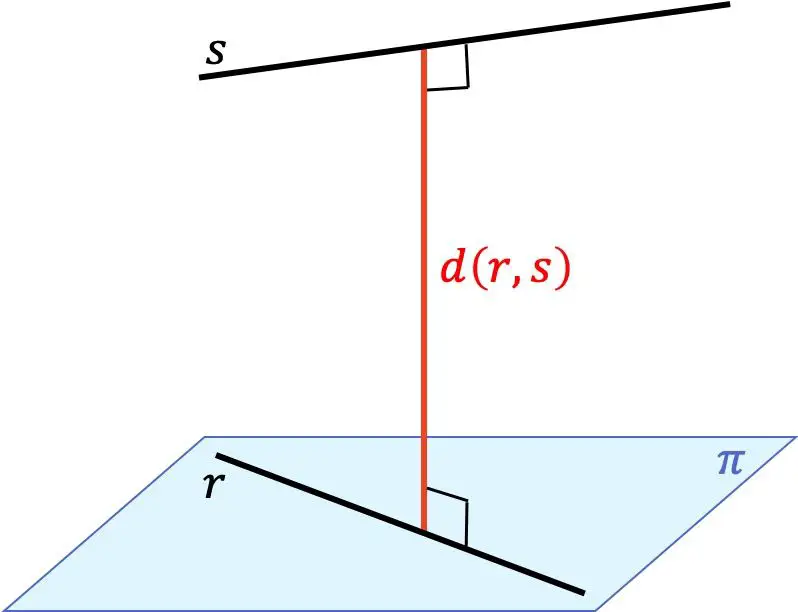
Das Ermitteln des Abstands zwischen zwei verschiedenen Linien im dreidimensionalen (3D) Raum hängt also von der relativen Position zwischen ihnen ab:
- Wenn die beiden Geraden zusammenfallen oder sich schneiden , ist der Abstand zwischen den beiden Geraden Null, da sie sich (mindestens) in einem Punkt schneiden.
- Wenn die beiden Linien parallel sind, müssen wir einen beliebigen Punkt auf einer der Linien nehmen und den Abstand zwischen diesem Punkt und der anderen Linie berechnen (unten finden Sie ein Beispiel dafür).
- Wenn sich die beiden Linien im Raum schneiden , müssen wir die Formel für den Abstand zwischen zwei sich schneidenden Linien anwenden (eine detaillierte Erklärung finden Sie unten).
Um also den Abstand zwischen zwei Linien zu berechnen, muss man zunächst wissen, um welche Art von Linien es sich handelt, und dann je nach Fall die eine oder andere Formel verwenden. Daher ist es wichtig, dass Sie bereits beherrschen , wie Sie die relative Position zweier Linien im Raum ermitteln, bevor Sie fortfahren. Wenn Sie sich jedoch nicht erinnern, wie es gemacht wurde, finden Sie im Link eine sehr vollständige Erklärung sowie Beispiele und gelöste Übungen Schritt für Schritt.
So ermitteln Sie den Abstand zwischen zwei parallelen Linien im Raum
Die Berechnung des Abstands zwischen zwei parallelen Linien im Raum (in R3) erfolgt auf die gleiche Weise wie in der Ebene (in R2): Sie müssen einen Punkt auf einer der beiden Linien nehmen und den Abstand dieses Punktes auf der anderen ermitteln Linie.
Somit lautet die Formel zur Berechnung des Abstands von einem Punkt zu einer Linie in drei Dimensionen (und zur Bestimmung des Abstands zwischen zwei parallelen Linien):
Gold:
-
ist der Betrag des Richtungsvektors der Linie
-
ist ein Punkt auf der Geraden
ein Punkt auf der Linie
Und
der durch die beiden Punkte definierte Vektor
-
ist die Größe des Kreuzprodukts zwischen den Vektoren
Und
Als Beispiel lösen wir ein Abstandsproblem zwischen zwei parallelen Linien im Raum:
- Wie groß ist der Abstand zwischen den folgenden zwei parallelen Geraden?
Beide Linien werden in Form einer Vektorgleichung ausgedrückt, daher können wir den Richtungsvektor und einen Punkt jeder von ihnen leicht herausfinden:
![\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-91c721e906a848c6c129721fe7908112_l3.png "Rendered by QuickLaTeX.com")
Wenn Sie Zweifel haben, wie Sie den Richtungsvektor und einen Punkt einer Linie bestimmen, empfehlen wir Ihnen, einen Blick auf die Erklärung der Liniengleichung zu werfen. Dort haben wir es für alle Geradengleichungen erklärt, denn das Finden des Richtungsvektors und eines Punktes, der zu einer Geraden gehört, hängt von der Art der Gleichung ab, in der die Gerade ausgedrückt wird.
Um nun den Abstand zwischen den beiden parallelen Linien zu ermitteln, müssen wir die Formel für den Abstand von einem Punkt zu einer Linie anwenden:
Wir berechnen also einerseits den Modul des Vektors, der sich aus dem Vektorprodukt ergibt. Wenn Sie Zweifel an der Berechnung haben, können Sie die Vektorproduktformel konsultieren, wo Sie außerdem Beispiele und gelöste Übungen dieser Operation zwischen Vektoren sehen können.
![\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f166cb84d794adae8b8e5678790a5ad8_l3.png "Rendered by QuickLaTeX.com")
Und andererseits finden wir die Größe des Vektors der Linie
Schließlich setzen wir den Wert jedes Termes in die Formel ein und berechnen den Abstand zwischen den Linien:
Daher beträgt der Abstand zwischen den beiden Linien 3,60 Einheiten.
So bestimmen Sie den Abstand zwischen zwei sich schneidenden Linien im Raum
Wie wir eingangs gesehen haben, unterscheidet sich die Methode zur Bestimmung des Abstands zwischen zwei sich schneidenden Geraden von der Vorgehensweise zur Bestimmung der Abstände zwischen parallelen Geraden.
Daher gibt es mehrere Methoden, um den Abstand zwischen zwei sich schneidenden Linien im Raum zu bestimmen. Auf dieser Seite erklären wir nur ein Verfahren, das einfachste, da die beiden anderen Methoden länger und komplizierter sind und praktisch nicht verwendet werden.
Der Richtungsvektor und ein beliebiger Punkt zweier Schnittlinien seien:
![\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-569f8d554a0f3704d247862d0b8ef852_l3.png "Rendered by QuickLaTeX.com")
Die Formel für den Abstand zwischen zwei sich schneidenden Geraden lautet:
![d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c613737cb66f811b123f886afd479e0a_l3.png "Rendered by QuickLaTeX.com")
Gold
![\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|](https://mathority.org/wp-content/ql-cache/quicklatex.com-dbc3e38427d29b2f4444ea732f955500_l3.png "Rendered by QuickLaTeX.com")
ist der Absolutwert des gemischten Produkts der Vektoren
und der durch die Punkte definierte Vektor
Und
. Und andererseits,
ist die Amplitude des Kreuzprodukts zwischen den Richtungsvektoren der beiden gekreuzten Linien.
Damit Sie sehen können, wie Sie den Abstand zwischen zwei sich kreuzenden Linien ermitteln, lösen wir beispielhaft eine Aufgabe:
- Wie groß ist der Abstand zwischen den nächsten beiden Schnittlinien?
Zuerst müssen wir den Richtungsvektor und einen Punkt auf jeder Linie identifizieren. Die beiden Geraden werden in Form einer kontinuierlichen Gleichung ausgedrückt, daher:
![\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b990f78d0263975304586abbd330167_l3.png "Rendered by QuickLaTeX.com")
Und jetzt wenden wir die Formel für den Abstand zwischen zwei Schnittlinien an:
Einerseits lösen wir das gemischte Produkt (oder dreifache Skalarprodukt):
![\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-c52c12945d04e320e688caf714569113_l3.png "Rendered by QuickLaTeX.com")
Und andererseits finden wir den Modul des Kreuzprodukts (oder Kreuzprodukts):
![\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-71afa7d4b49e542300c12b5263858665_l3.png "Rendered by QuickLaTeX.com")
Schließlich ersetzen wir den Wert jedes Termes in der Formel durch den Abstand zwischen zwei gekreuzten Linien:
![d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0aac39997c35738e8e84a29ff7c97c6_l3.png "Rendered by QuickLaTeX.com")
