Abstand zwischen einem Punkt und einer Linie

Hier finden Sie die Formel zur Berechnung des Abstands zwischen einem Punkt und einer Linie. Darüber hinaus können Sie mehrere Beispiele und gelöste Übungen zu Abständen zwischen Punkten und Linien und sogar die Anwendungen sehen, die diese Operation hat (z. B. Ermitteln des Abstands zwischen parallelen Linien).

Formel für den Abstand zwischen einem Punkt und einer Linie

Der Abstand zwischen einem Punkt und einer Linie ist der kürzeste Abstand zwischen diesem Punkt und der Linie. Mathematisch entspricht dieser Mindestabstand der Länge des vom Punkt zur Linie gezogenen Segments, das senkrecht zur Linie verläuft.

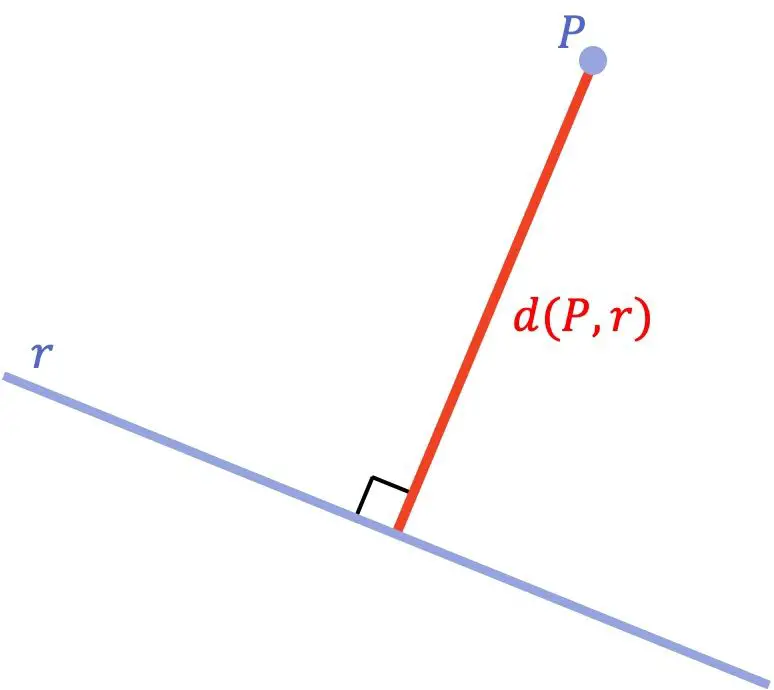
Wie groß ist der Abstand zwischen einem Punkt und einer Linie?

Nachdem wir das geometrische Konzept des Abstands zwischen einem Punkt und einer Linie kennengelernt haben, schauen wir uns an, welche Formel zur Berechnung dieses Abstands verwendet wird:

Gegeben sei die implizite (oder allgemeine) Gleichung einer Geraden und der Koordinaten eines beliebigen Punktes auf einer Ebene:

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

Die Formel für den Abstand zwischen einem Punkt und einer Linie lautet:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Wichtig: Beachten Sie, dass die Gleichung der Geraden in der Formel die Form einer impliziten (oder allgemeinen) Gleichung hat. Wenn wir also die Gerade in einem anderen Gleichungstyp ausgedrückt haben, müssen wir sie zuerst an ihre implizite Gleichung und dann weitergeben Wir können die Formel anwenden.

Beispiel für die Berechnung des Abstands zwischen einem Punkt und einer Linie

Unten sehen Sie ein Beispiel für die Berechnung des Abstands zwischen einem Punkt und einer Linie:

Finden Sie den Abstand zwischen dem Punkt
$P$

und das Gesetz

$r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

Um den Abstand zwischen dem Punkt und der Linie zu berechnen, wenden Sie einfach die Formel an:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Jetzt ersetzen wir jeden Begriff durch seinen Wert:

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

Und schließlich berechnen wir die Entfernung:

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

Abstand zwischen zwei parallelen Linien

Eine der Anwendungen zur Berechnung des Abstands zwischen einer Linie und einem Punkt besteht darin, den Abstand zwischen parallelen Linien zu ermitteln.

Um das Konzept zu verstehen, das wir im Folgenden erläutern werden, müssen Sie natürlich wissen , was parallele Linien sind . Wenn Sie also ihre Definition nicht genau kennen, hinterlassen wir Ihnen einen Link, in dem wir sie im Detail erklären und Sie können auch Beispiele sehen aus parallelen Linien.

Um den Abstand zwischen zwei parallelen Geraden zu ermitteln, nehmen Sie einfach einen Punkt auf einer der beiden Geraden und berechnen Sie den Abstand von diesem Punkt zur anderen Geraden.

Abstand zwischen einem Punkt und einer Linie

Um den Abstand zwischen zwei parallelen Geraden zu bestimmen, wird also auch die Formel für den Abstand zwischen einer Geraden und einem Punkt verwendet.

Wenn wir andererseits bei Verwendung der Formel einen Abstand von 0 Einheiten erhalten, bedeutet dies, dass sich die Linien an einem bestimmten Punkt berühren und daher nicht parallel sind, sondern sich schneiden, zusammenfallen oder senkrecht stehen. Wenn Sie möchten, können Sie die Unterschiede zwischen dieser Art von Leitungen auf unserer Website überprüfen.

Sehen wir uns also anhand eines Beispiels an, wie man ein Abstandsproblem zwischen zwei parallelen Linien löst:

Ermitteln Sie den Abstand zwischen den folgenden zwei parallelen Geraden:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Als Erstes müssen wir einen Punkt auf einer der Linien (der gewünschten) erreichen. In diesem Fall berechnen wir einen Punkt auf der Linie

$s.$

Dazu müssen Sie einer der Variablen einen Wert zuweisen, wie wir es beispielsweise tun werden

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Und jetzt löschen wir die andere Variable (

$y$

) der erhaltenen Gleichung, um zu wissen, wie viel sie zu diesem Zeitpunkt wert ist:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Daher wird der Punkt aus der Linie erhalten

$s$

Ost:

$P(0,-2)$

Und sobald wir bereits einen Punkt auf einer Geraden haben, berechnen wir den Abstand von diesem Punkt zur anderen Geraden mit der Formel:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

Probleme mit dem Abstand zwischen einem Punkt und einer Linie gelöst

Übung 1

Berechnen Sie den Abstand zwischen den Punkten

$P$

und das Gesetz

$r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

siehe Lösung

Um den Abstand zwischen einem Punkt und einer Linie zu ermitteln, wenden Sie einfach die Formel an:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Wir ersetzen jeden Term durch seinen Wert und berechnen den Abstand:

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

Übung 2

Wie groß ist der Abstand zwischen dem Punkt

$P$

und das Gesetz

$r$

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

siehe Lösung

In diesem Fall liegt die Geradengleichung in impliziter (oder allgemeiner) Form vor. Um stattdessen die Formel für den Abstand von einem Punkt zu einer Linie verwenden zu können, muss die Linie als implizite Gleichung ausgedrückt werden. Wir müssen daher zunächst die Gerade transformieren und an eine implizite Gleichung übergeben (übergeben Sie einfach alle Terme auf derselben Seite der Gleichung):

$r: \ 3x+y-5=0$

Und sobald die Linie bereits in expliziter Form vorliegt, können wir nun die Formel für den Abstand zwischen einem Punkt und einer Linie verwenden:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Wir ersetzen daher jeden Term durch seinen Wert und berechnen den Abstand:

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

Übung 3

Wie groß ist der Abstand zwischen den folgenden beiden Linien?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

siehe Lösung

Zuerst werden wir überprüfen, ob es sich um zwei parallele Linien handelt. Hierzu die Koeffizienten der Variablen

$x$

Und

$y$

müssen proportional zueinander sein, jedoch nicht zu den unabhängigen Termen:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

Da die Linien tatsächlich parallel sind, können wir das Verfahren anwenden.

Jetzt müssen wir einen Punkt von einer der Linien (der gewünschten) erhalten. In diesem Fall berechnen wir einen Punkt auf der Linie

$s.$

Dazu müssen Sie einer der Variablen einen Wert zuweisen, wie wir es beispielsweise tun

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

Und jetzt löschen wir die andere Variable (

$y$

) der erhaltenen Gleichung, um ihren Wert an diesem Punkt zu kennen:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

Damit ergibt sich der Punkt aus der Geraden

$s$

Ost:

$P(0,-1)$

Sobald wir einen Punkt auf einer Linie kennen, berechnen wir den Abstand von diesem Punkt zur anderen Linie mit der Formel:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

Übung 4

Berechnen Sie den Wert der Unbekannten

$k$

so dass der Abstand zwischen dem Punkt

$P$

und das Gesetz

$r$

also 5 Einheiten.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

siehe Lösung

Wir müssen zunächst die Formel für den Abstand zwischen einem Punkt und einer Linie anwenden:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Jetzt ersetzen wir jeden Term durch seinen Wert und vereinfachen den Ausdruck:

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

Die Problemstellung sagt uns, dass der Abstand zwischen dem Punkt und der Linie gleich 5 sein muss, also setzen wir den vorherigen Ausdruck auf 5:

$\cfrac{\lvert -49+k\rvert}{13}=5$

Und wir lösen die resultierende Gleichung. Im Zähler des Bruchs steht ein Absolutwert, daher müssen wir getrennt analysieren, wann der Absolutwert positiv und wann negativ ist:

$\cfrac{+(-49+k)}{13}=5$