Ableitung eines produkts (oder multiplikation)

In diesem Artikel erklären wir, wie man das Produkt zweier Funktionen (Formel) herleitet. Darüber hinaus können Sie mehrere Beispiele für Ableitungen von Funktionsprodukten sehen und sogar mit gelösten Übungen zu Multiplikationsableitungen üben.

Formel für die Ableitung eines Produkts

Die Ableitung eines Produkts zweier verschiedener Funktionen ist gleich dem Produkt der Ableitung der ersten Funktion mit der zweiten undifferenzierten Funktion plus dem Produkt der ersten undifferenzierten Funktion mit der Ableitung der zweiten Funktion.

Mit anderen Worten: Wenn f(x) und g(x) zwei verschiedene Funktionen sind, lautet die Formel für die Ableitung der Multiplikation zwischen den beiden Funktionen wie folgt:

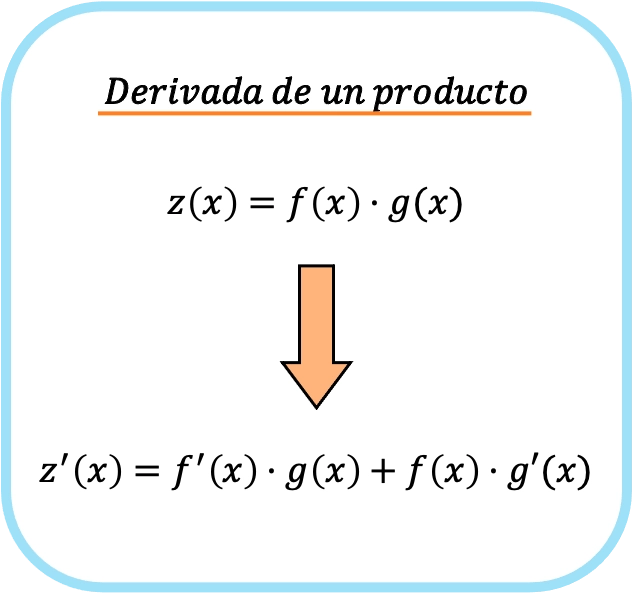
Wenn wir also die Regel der Ableitung eines Produkts anwenden, gelangen wir von einer einfachen Multiplikation zu zwei verschiedenen Produkten.

Beispiele für Derivate eines Produkts

Sobald wir wissen, wie die Formel für die Ableitung eines Produkts (oder eine Multiplikation) lautet, werden wir mehrere Beispiele für diese Art von Ableitung lösen. Dadurch wird es für Sie viel einfacher zu verstehen, wie ein Produkt zweier Funktionen abgeleitet wird.

Beispiel 1

In diesem Beispiel lösen wir die Ableitung zweier potentieller Funktionen durch Multiplikation:

Wie wir im vorherigen Abschnitt gesehen haben, lautet die Formel für die Ableitung der Multiplikation:

Daher müssen wir zunächst die Ableitung jeder Funktion separat berechnen:

Und sobald wir die Ableitung jeder Funktion kennen, können wir die Formel für die Ableitung des Produkts zweier Funktionen anwenden. Das heißt, wir multiplizieren die Ableitung des ersten Faktors mit dem zweiten Faktor, ohne zu differenzieren, und addieren dann das Produkt des ersten Faktors, ohne zu differenzieren, mit der Ableitung des zweiten Faktors:

Abschließend führen wir die Operationen aus, um das erhaltene Ergebnis zu vereinfachen:

Beispiel 2

In diesem Fall leiten wir das Produkt einer Konstante durch eine Funktion ab:

Die Ableitungsregel eines Produkts lautet wie folgt:

Daher leiten wir jede Funktion, die Teil des Produkts ist, separat ab:

Und dann wenden wir die Regel für die Ableitung einer Multiplikation an:

Beachten Sie, dass die Ableitung einer Konstante immer Null ist. Daraus können wir schließen, dass die Ableitung der Multiplikation einer Konstante mit einer Funktion gleich dem Produkt aus der Konstante und der Ableitung der Funktion ist.

Beispiel 3

Lösen wir das Produkt zwischen einer Exponentialfunktion und einem natürlichen Logarithmus:

Die Formel für die Ableitung einer Multiplikation zweier Funktionen lautet:

Wir müssen daher zunächst separat die Ableitung jeder Funktion bilden, die das Produkt bildet, und zwar wie folgt:

Das abgeleitete Produkt der Funktionen ist daher:

Gelöste Übungen zur Ableitung eines Produkts

Leitet die folgenden Funktionsprodukte ab:

Abgeleitet von einem Produkt mit drei Funktionen

Als nächstes überlassen wir Ihnen die Formel für die Ableitung der Multiplikation von drei Funktionen, da sie der von zwei Funktionen sehr ähnlich ist und in manchen Fällen nützlich sein kann.

Die Ableitung eines Produkts von drei Funktionen ist gleich dem Produkt der Ableitung der ersten Funktion und der anderen beiden Funktionen plus dem Produkt der Ableitung der zweiten Funktion und der anderen beiden Funktionen plus dem Produkt der Ableitung der dritte Funktion.Funktion durch die anderen beiden Funktionen.

Wenn wir beispielsweise die folgende Multiplikation von drei verschiedenen Funktionen ableiten möchten:

Um die Ableitung zu lösen, müssen wir die Regel der Ableitung des Produkts dreier Funktionen anwenden, also:

Demonstration der Formel für die Ableitung eines Produkts

Abschließend zeigen wir die Formel für die Ableitung einer Multiplikation. Man muss es sich nicht merken, aber es ist immer gut zu verstehen, woher die Formeln kommen. 🙂

Aus der mathematischen Definition der Ableitung:

Die Funktion z sei das Produkt zweier verschiedener Funktionen:

Dann ist die Ableitung von z laut Definition:

Wie wir wissen, hat das Addieren eines Termes durch Addieren und Subtrahieren keinen Einfluss auf das Ergebnis, solange es sich bei beiden um denselben Term handelt. Wir können also zum nächsten Schritt übergehen:

Wir verwenden nun die Grenzeigenschaften, um die vorherige Grenze in zwei verschiedene Grenzen zu trennen:

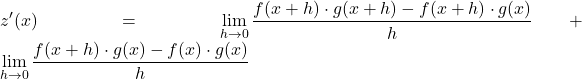
Wir extrahieren den gemeinsamen Faktor im Zähler der beiden Brüche:

Andererseits kennen wir das Ergebnis der folgenden Grenze:

Daher können wir die Grenzen vereinfachen:

Betrachtet man schließlich die beiden verbleibenden Grenzwerte, entspricht jeder der Definition der Ableitung einer Funktion. Die Gleichstellung kann daher vereinfacht werden:

Oder gleichwertig: